
复变函数二、解析函数导数的几何意义设w= f(z)在区域D内解析,zo D,且 f(z)≠ 0.1.Argf(zo)的几何意义C:z平面内过z的有向光滑曲线参数方程:y (z)z=z(t), (α≤t≤β);z'(to)正向:t增大的方向:c且 Zo = z(to),Zoz'(t)± 0,α<z<β.x0u
6 二、解析函数导数的几何意义 1. Argf (z0 )的几何意义 : , : C z平面内过z0的有向光滑曲线 参数方程 z = z(t), ( t ); 正向: t 增大的方向; ( ), 0 0 且 z = z t ( ) 0, . z t 0 z C 0 z . y 0 x (z) 设w = f (z)在区域D内解析, ( ) 0 z t , ( ) 0. z0 D 且 f z0
复变函数映射w= f(z)将C映射成w平面内过wo= f(zo)的有向光滑曲线,其参数方程为w=f[z(t)l,α<z<β,正向:t增大的方向,W=f(z)y (z)y (w)z'(to))TcCZowoxx00U
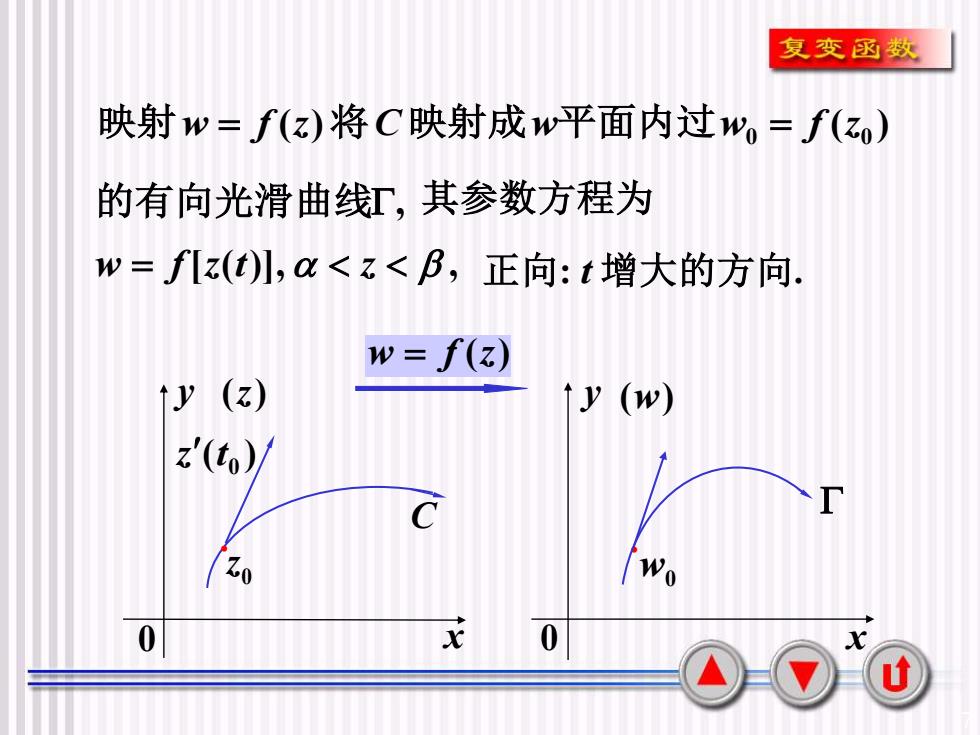
7 的有向光滑曲线, 其参数方程为 w = f[z(t)], z , 正向: t 增大的方向. ( ) ( ) 0 0 映射w = f z 将C 映射成w平面内过w = f z C 0 z . y 0 x (z) ( ) 0 z t y 0 x (w) w0 . w = f (z)