曲线y=f(x)(C0)与直线x=a,x=b(a<b) 及x轴所围曲边梯形面积 y↑y=f(x 元素法: 积分变量:x 积分区间:【a,b] 面积元素: △s≈f(x)dx=d4 oa x b x 所求面积: A=d 微小的局部 “以直代曲” 定积分几何意义x+dx ◆例1计算由两条抛物线:y2=x、Jy户x2 所围成的图形的面积 分析:积分变量:x积分区间:0,1] 面积元素: △S≈(N-x2)dx 所求面积: 4=J(-x)dx xx+dxl
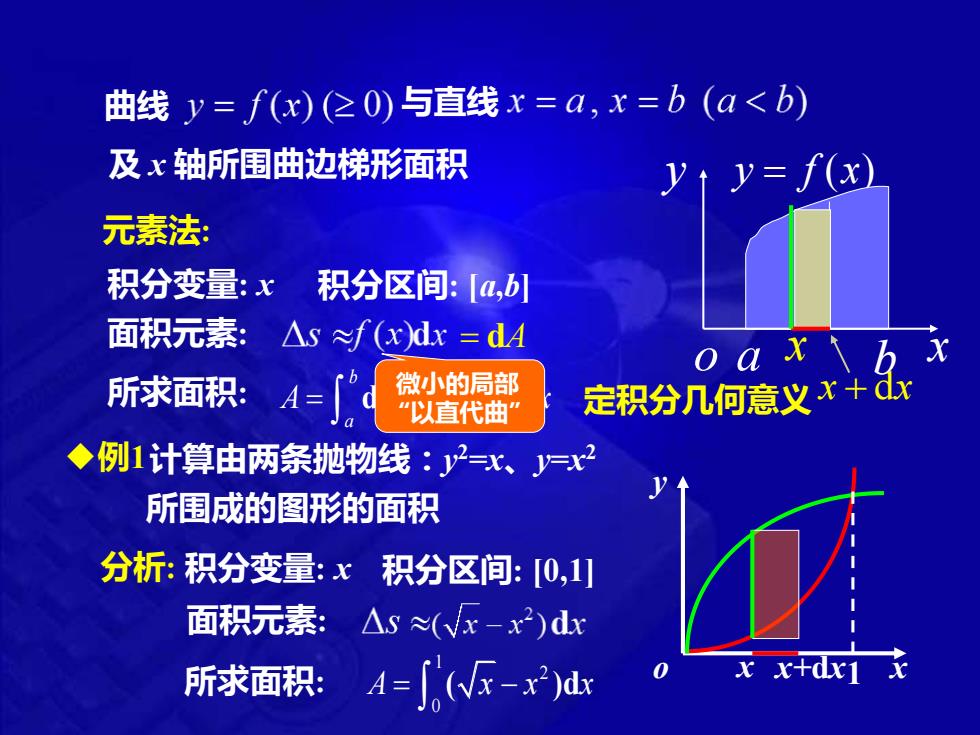
曲线 与直线 及 x 轴所围曲边梯形面积 定积分几何意义 o a b x y y = f (x) x x + dx 元素法: 积分变量: x 积分区间: [a,b] 面积元素: = dA 所求面积: d ( ) d b b a a A A f x x = = 微小的局部 “以直代曲” ◆例1计算由两条抛物线:y 2=x、y=x 2 所围成的图形的面积 o x y x x+dx1 分析: 积分变量: x 积分区间: [0,1] 面积元素: 所求面积: 1 2 0 A x x x = − ( )d
◆例2计算由抛物线2-2x与直线=x-4 所围成的图形的面积 分析:法一 y+dy 积分变量:y积分区间:-2,4 面积元素 :dA=0+4-y2)d -2 所求面积: A=可广04-2y
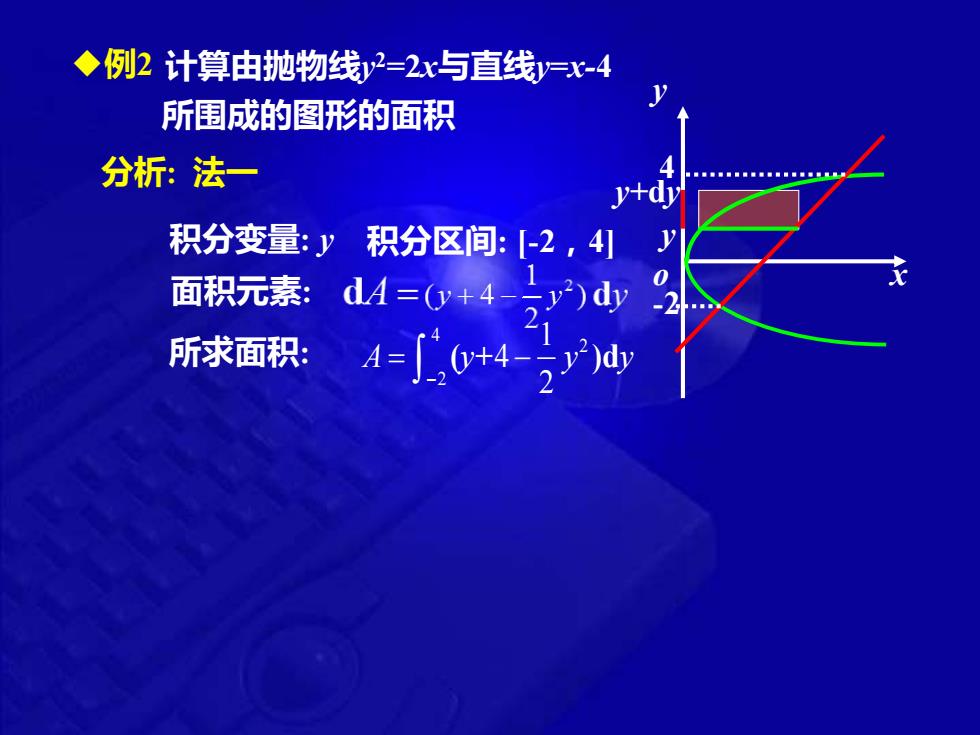
◆ 例 2 计算由抛物线y 2=2 x与直线y =x- 4 所围成的图形的面积 o x yy y+ dy 积分变量: y 分析 : 积分区间: [ - 2 ,4] 面积元素 : 所求面积 : 4 2 2 1 4 2 A y y y ( + )d − = − - 2 法一 4