
第八讲逯数图形的描绘
第八讲 函数图形的描绘

函数图形的描绘 一、函数的性态 二、函数图形的描绘
函数图形的描绘 一、函数的性态 二、函数图形的描绘

函数图形的描绘 丞数的性态 二、函数图形的描绘
函数图形的描绘 一、函数的性态 二、函数图形的描绘

>函数的性态 特性 性态 研究工具 关键点 定义域 自变量变化范围 无定义的点 整 值域 函数取值范围 初等方法 体 奇偶性 图形的对称性 有 周期性 图形的平移性 限 连续性 图形的连续性 极限 间断点、零点 局 单调性 图形的升降 一阶导数 极值点 二阶导数 拐点 无 凸凹性 图形的弯曲方向 限 渐近线 图形的变化趋势 极限
➢函数的性态 特性 性态 关键点 定义域 自变量变化范围 值域 函数取值范围 奇偶性 图形的对称性 周期性 图形的平移性 单调性 图形的升降 凸凹性 连续性 图形的连续性 图形的弯曲方向 渐近线 图形的变化趋势 研究工具 初等方法 极限 一阶导数 二阶导数 极限 无定义的点 间断点、零点 极值点 拐点 整 体 局 部 有 限 无 限
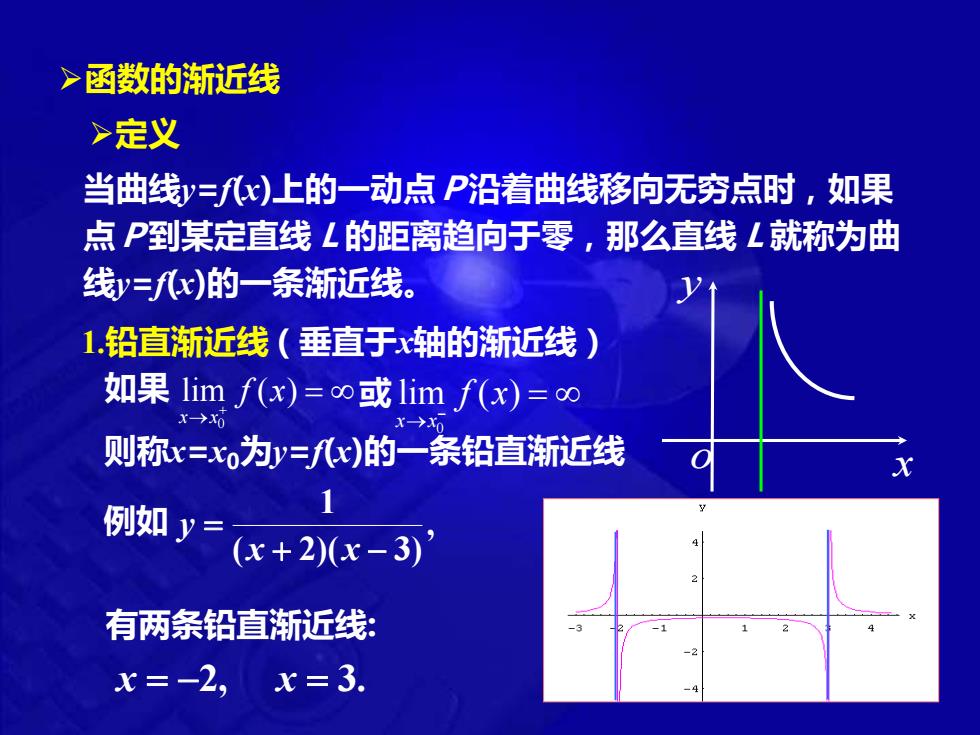
函数的渐近线 >定义 当曲线=八x)上的一动点P沿着曲线移向无穷点时,如果 点P到某定直线L的距离趋向于零,那么直线L就称为曲 线y三fx)的一条渐近线。 1铅直渐近线(垂直于x轴的渐近线) 如果limf(x)=∞或1imf(x)=o∞ 则称x=xo为y=f孔x)的一条铅直渐近线 例如y= 1 (x+2)(x-3) 有两条铅直渐近线: x=-2, x=3
0 lim ( ) x x f x → + 如果 = 或 0 lim ( ) x x f x → − = ➢定义 1.铅直渐近线 当曲线y=f(x)上的一动点P沿着曲线移向无穷点时,如果 点P到某定直线L的距离趋向于零,那么直线L就称为曲 线y=f(x)的一条渐近线。 (垂直于x轴的渐近线) 则称x=x0为y=f(x)的一条铅直渐近线 ➢函数的渐近线 x y o 例如 , ( 2)( 3) 1 + − = x x y 有两条铅直渐近线: x = −2, x = 3