
第二讲数量积向量积
第二讲 数量积 向量积

数量积向量积 两向量的数量积 二、两向量的向量积
数量积 向量积 一、两向量的数量积 二、两向量的向量积

数量积向量积 两向量的数量积 二、两向量的向量积
数量积 向量积 一、两向量的数量积 二、两向量的向量积
>引例 设一物体在常力F作用下,沿与力夹角为日的直线移动, 位移为,则力所做的功为 w =Fs coso ~e M M, >定义 设向量a,b的夹角为9,称abcos0为a与b的 数量积(点积),记作a,b ●注当a≠0时,bcos0=Prja B一(在a让的投影) ->a.b=a Prjab 类似地a.乙=bPrj5a(b≠0)
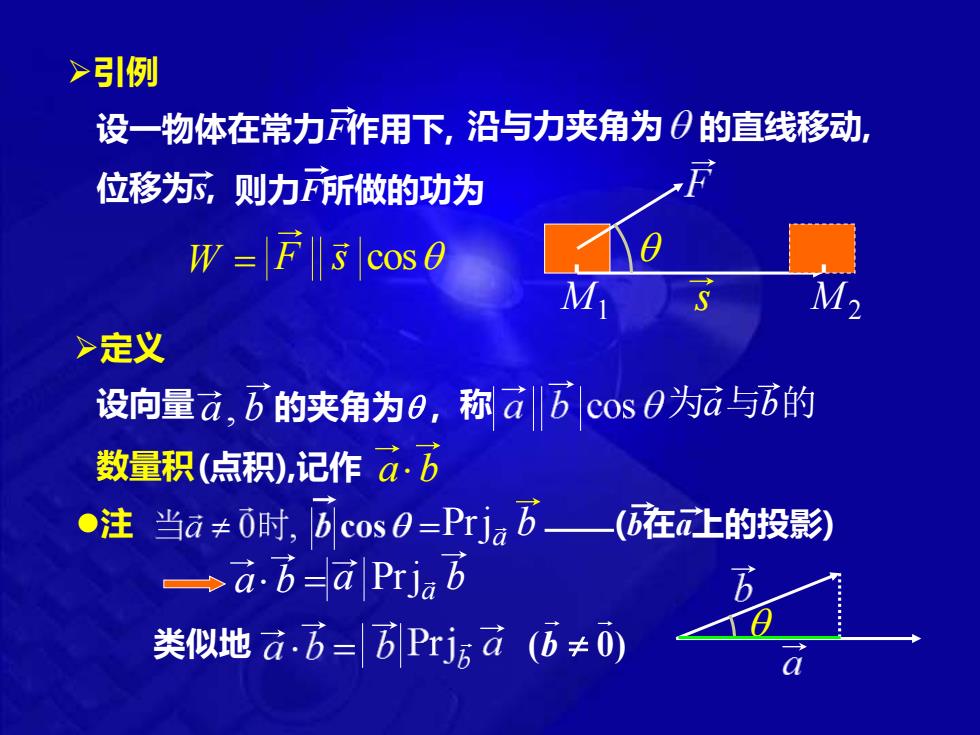
M1 W = ➢定义 F s cos M2 a b 设向量 的夹角为 , 称 数量积(点积),记作 a, b 为a与b的 s ➢引例 设一物体在常力F作用下, 沿与力夹角为 的直线移动, 位移为s, 则力F所做的功为 ⚫注 Prja b a b = a Prja b ( 0) 类似地 b (b在a上的投影)

>性质 (1)a.a-ap (2)a,b为两个非零向量,则有a方=0←→a16 >运算律 (1)交换律 a.b-ba (2)结合律 (2,4为实数) (2a)b=a:(2b=2(a.b (Aa)(uB)=Au(a.B) Prjca Prje b (3)分配律 (a+b)c-a.c+b.c Prjz(@+B) ◆例1证明三角形余弦定理c2=a2+b2-2 ab cos0
➢性质 为两个非零向量, 则有 (1) a a = (2) a,b a b = 0 ⊥ ➢运算律 (1)交换律 (2)结合律 a ( b) ( a)( b) = (a b) (3)分配律 c a b + b a a Prj c b c Prj Prj (a b) c + ◆例1证明三角形余弦定理 2 cos . 2 2 2 c = a +b − ab