
第四讲 反常积分
第四讲 反常积分

反常积分 一、无穷限的反常积分 二、无界函数的反常积分
反常积分 一、无穷限的反常积分 二、无界函数的反常积分

反常积分 一、无穷限的反常积分 二、无界函数的反常积分
反常积分 一、无穷限的反常积分 二、无界函数的反常积分
>引例 曲线y=三和直线X=1及x轴所围成的开口曲边梯形的面积 -》 记作: 无穷限的反常积分
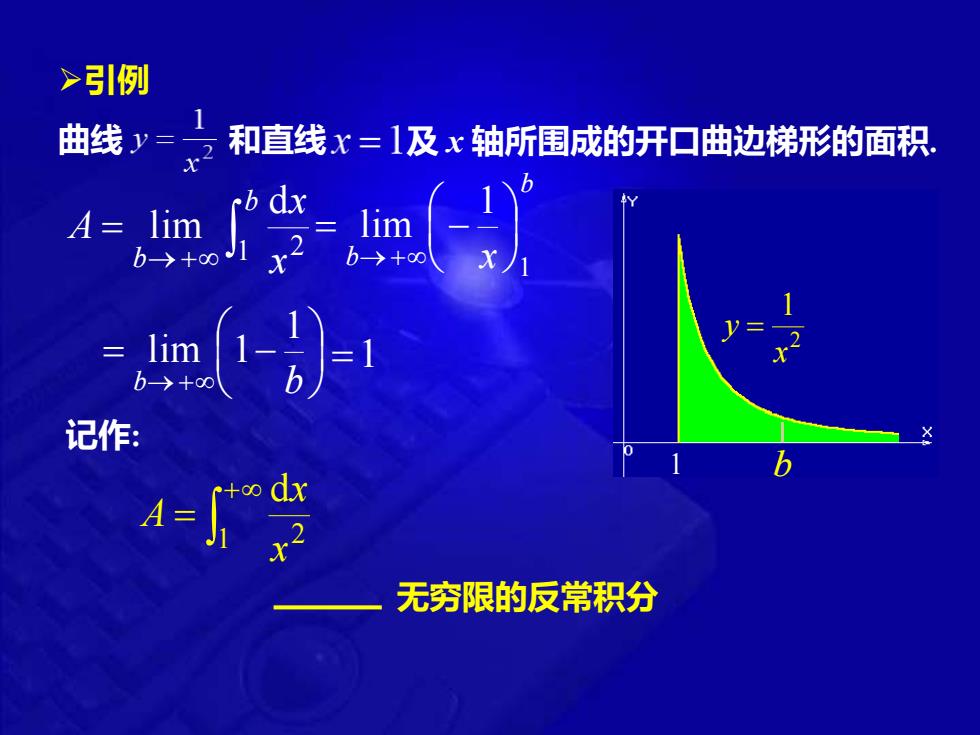
2 1 x y = 1 b 曲线 和直线 及 x 轴所围成的开口曲边梯形的面积. + = 1 2 d x x A →+ = b b x x A 1 2 d lim b b x 1 1 lim = − →+ = − b→+ b 1 lim 1 =1 ➢引例 记作: 无穷限的反常积分

设f(x)∈C[a,+oo),任取t>a, ()dx 函数f(x)在无穷区间[4,+o)上的反常积分 记为∫”f(x)dk,即f(x)dx-lim∫f(x)dx >定义(反常积分“fx)dc的收敛与发散) 设函数f(x)在区间[a,+o∞)上连续,如果上述极限存在,那么 称反常积分∫。f(x)收敛;并称此极限为该反常积分的值; 如果上述极限不存在,那么称反常积分f(x)dx发散
函数 f (x) 在无穷区间[a,+∞)上的反常积分 设 f (x)C[a, + ), 任取 t a , 记为 即 称反常积分 收敛 ; 如果上述极限不存在, 那么称反常积分 发散 . 并称此极限为该反常积分的值; 设函数 f (x) 在区间[a,+∞)上连续,如果上述极限存在,那么 ➢定义 (反常积分 ( )d 的收敛与发散) a f x x +