
第四讲有理数的积分
第四讲 有理函数的积分

有理函数的积分 一、 有理丞数的积分 二、可化为有理函数的积分
有理函数的积分 一、有理函数的积分 二、可化为有理函数的积分

有理函数的积分 一、有理巫数的积分 二、可化为有理数的积分
有理函数的积分 一、有理函数的积分 二、可化为有理函数的积分
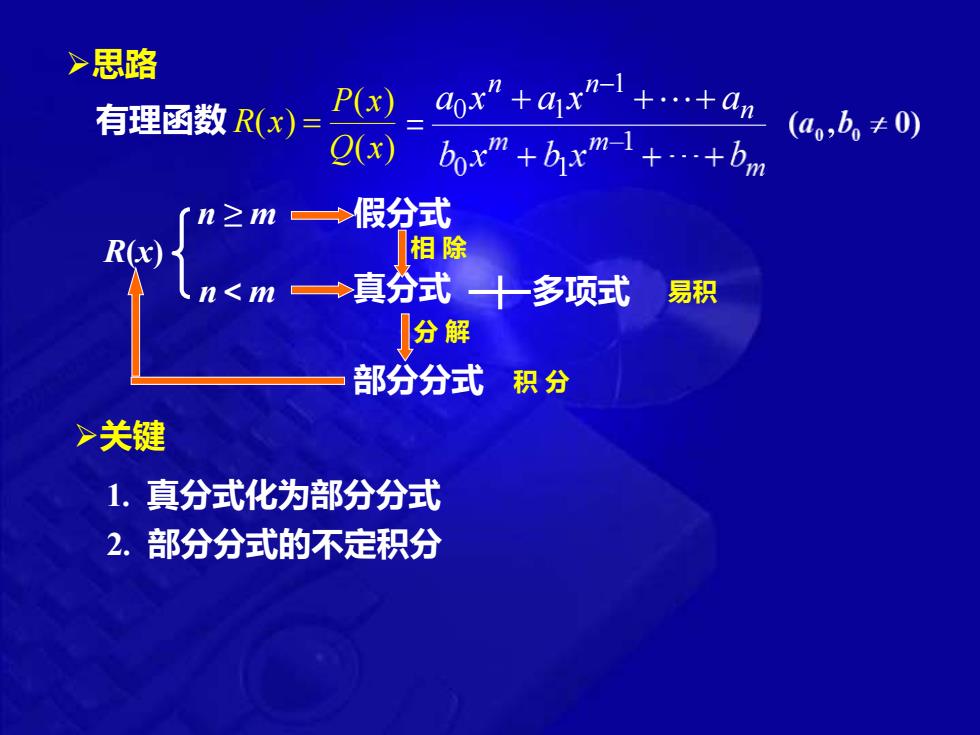
>思路 有理函数R(x)= P-a0x”+a4x++a e(x) box+x+bm (ao,b≠0) n≥n →假分式 R(x) 相除 n<m →真分式十多项式 易积 分解 部分分式积分 >关键 1.真分式化为部分分式 2.部分分式的不定积分
➢思路 ( ) ( ) ( ) Q x P x R x = = n n n a x + a x + + a 0 1 −1 有理函数 R(x) n ≥ m n<m 假分式 真分式 相 除 多项式 易积 分 解 部分分式 积 分 ➢关键 1. 真分式化为部分分式 2. 部分分式的不定积分
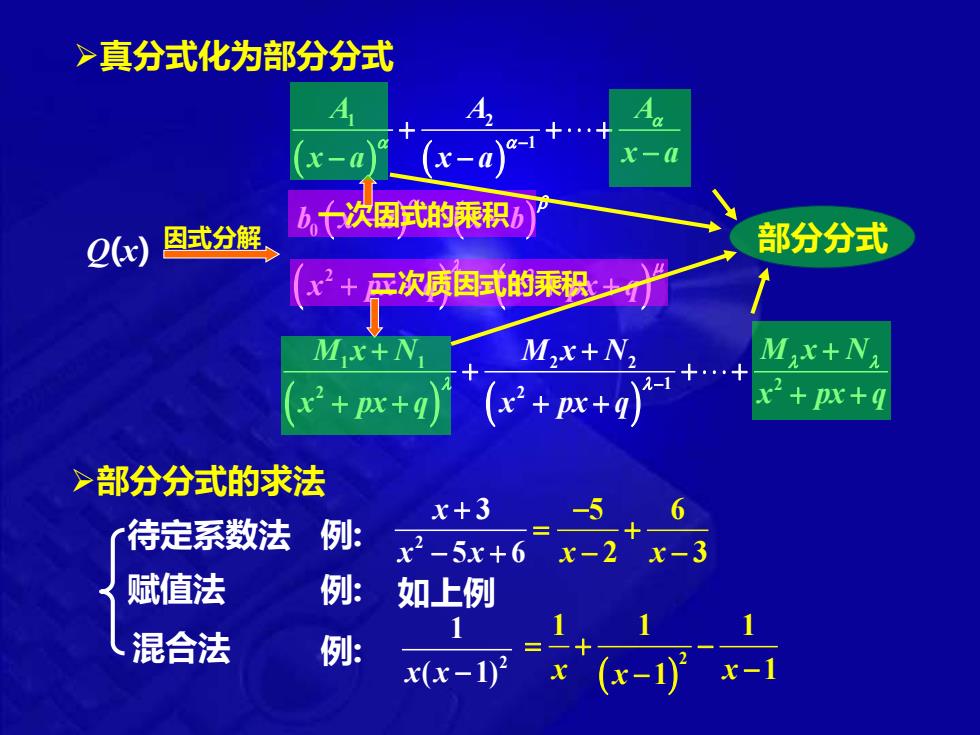
>真分式化为部分分式 b七次困式的乘积 2x) 因式分解 部分分式 工次质因式的乘积 Mx+N M,x+N, M,x+N +px+q (x2+px+q +px+q >部分分式的求法 x+3 -5 待定系数法 例: +6 x2-5x+6x-2+x-3 赋值法 例: 如上例 1 混合法 例: x(x-1x(x-1 x-
➢真分式化为部分分式 Q(x) 因式分解 ( ) ( ) 0 b x a x b − − ( ) ( ) 2 2 x px q x px q + + + + ( ) ( ) 1 2 1 A A A x a x a x a − + + + − − − ( ) ( ) 1 1 2 2 1 2 2 2 M x N M x N M x N x px q x px q x px q − + + + + + + + + + + + + 一次因式的乘积 二次质因式的乘积 部分分式 ➢部分分式的求法 待定系数法 例: 2 3 5 6 x x x + − + 5 6 x x 2 3 − = + − − 赋值法 例: 2 1 x x( 1) − 混合法 例: 如上例 ( ) 2 1 1 1 x x x 1 1 = + − − −