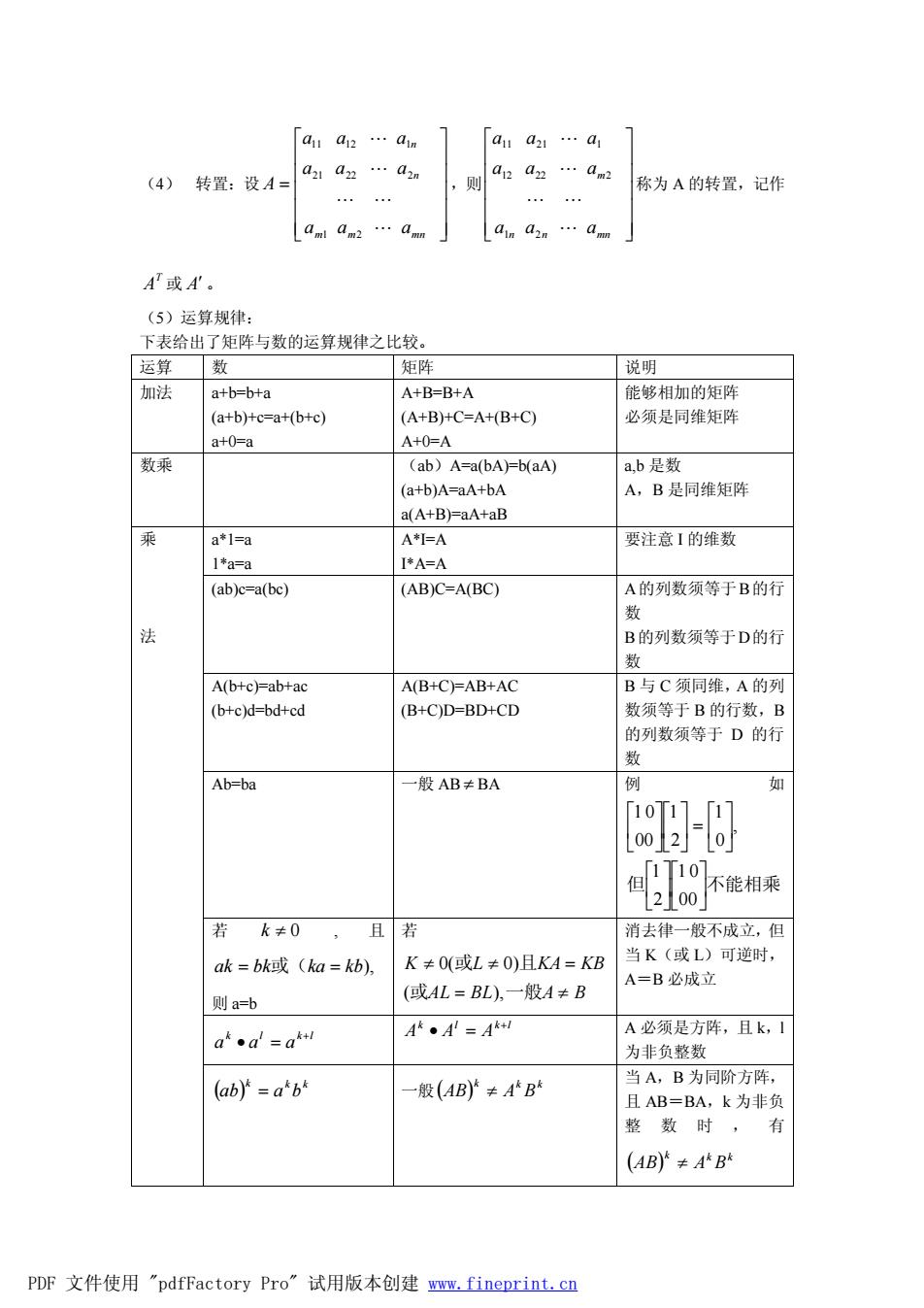
a1a2…aim [aa21…a (4)转置:设A= aan…a2n 称为A的转置,记作 A或N (5)运算规律 下表给出了矩阵与数的运算规律之比较, 运算 新 矩阵 说明 加法 a+b-bta A+B-B+A 能铭相加的矩阵 (a+b)+c-a+(b+c) (A+B)+C-A+(B+C) 必须是同维矩阵 a+0=a A+0=A 数乘 (ab)A=a(bA)=b(aA) a.b是数 (a+b)A=aA+bA A,B是同维矩阵 a(A+B)=aA+aB 乘 a*1=a A*I=A 要注意1的维数 】*a=a I'A=A (ab)c=a(bc) (AB)C=A(BC) A的列数须等于B的行 勒 B的列数须等于D的行 A(b+c)=ab+ac A(B+CEAB+AC B与C须同维,A的列 (b+c)d=bd+cd (B+C)D=BD+CD 数须等于B的行数,B 的列数须等于D的行 Ab-ba 般AB≠BA 阿 如 [10T1111 0o2F0 的ee 若k≠0, 且若 消去律一般不成立,但 ak=bk或(ka=b), K≠0(或L≠O)且KA=KB 当K(或L)可逆时, A=B必成立 则a=b (或AL=BL),一般A≠B aa=a A·A=A A必须是方阵,且k, 为非负整数 (ab)"=a'b 一般(AB)≠AB 当A,B为同阶方阵, 且AB=BA,k为非负 整数时, (AB)≠AB PDF文件使用”pdfFactory Pro”试用版本创建,fineprint,cn
(4) 转置:设 ú ú ú ú ú û ù ê ê ê ê ê ë é = m m mn n n a a a a a a a a a A L L L L L 1 2 21 22 2 11 12 1 ,则 ú ú ú ú ú û ù ê ê ê ê ê ë é n n mn m a a a a a a a a a L L L L L 1 2 12 22 2 11 21 1 称为 A 的转置,记作 T A 或 A¢ 。 (5)运算规律: 下表给出了矩阵与数的运算规律之比较。 运算 数 矩阵 说明 加法 a+b=b+a (a+b)+c=a+(b+c) a+0=a A+B=B+A (A+B)+C=A+(B+C) A+0=A 能够相加的矩阵 必须是同维矩阵 数乘 (ab)A=a(bA)=b(aA) (a+b)A=aA+bA a(A+B)=aA+aB a,b 是数 A,B 是同维矩阵 a*1=a 1*a=a A*I=A I*A=A 要注意 I 的维数 (ab)c=a(bc) (AB)C=A(BC) A的列数须等于B的行 数 B的列数须等于D的行 数 A(b+c)=ab+ac (b+c)d=bd+cd A(B+C)=AB+AC (B+C)D=BD+CD B 与 C 须同维,A 的列 数须等于 B 的行数,B 的列数须等于 D 的行 数 Ab=ba 一般 AB ¹ BA 例 如 但 ú不能相乘 û ù ê ë é ú û ù ê ë é ú û ù ê ë é =ú û ù ê ë é ú û ù ê ë é 00 1 0 2 1 , 0 1 2 1 00 1 0 若 k ¹ 0 , 且 ak = bk或(ka = kb), 则 a=b 若 AL BL A B K L KA KB = ¹ ¹ ¹ = 或 一般 或 且 ( ), 0( 0) 消去律一般不成立,但 当 K(或 L)可逆时, A=B 必成立 k l k l a a a + · = k l k l A A A + · = A 必须是方阵,且 k,l 为非负整数 乘 法 ( ) k k k ab = a b 一般( ) k k k AB ¹ A B 当 A,B 为同阶方阵, 且 AB=BA,k 为非负 整 数 时 , 有 ( ) k k k AB ¹ A B PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

转置 (4Y=A A,B为同维矩阵, k为数 (A+B)=4+B A的列数须等于B的行 (kA)=kA (AB)=BA 1.13矩阵的初等变换与初等矩阵 (1)矩阵A的初等变换有如下三类 第一类:将A的第i行(列)与第j行(列)对换,记为,C): 第二类:以非零常数k乘A的i行(列),记作r(k)C,(k)。 第三类:将A的第i行(列的k倍加到第j行(列)上去,记作,化北k): (2)初等矩阵是单位阵1经过一次初等变换后得到的矩阵 1R,1RW,1因)R, 1S6,1c国e.1R (4)初等变换与初等矩阵之间的关系 (5)初等矩阵左(右)乘A,相当与对A进行一次相应的初等行(列)变换,例如: AB台R,AB,ASB台4C,=B. 注1若矩阵A经过有限次初等变换得到矩阵B,则称B与A等价,此时必有等式 R,…RAC,…C,=B成立,其中R,…R和C,…C,均为初等矩阵 注2任一矩阵A经有限次初等变换后均可化为形如[0]的矩阵,其中1为A的铁,称 L00 1.1.4可逆矩阵的定义 设A为n阶方阵,若存在n阶方阵B,使AB=BA=I,则称A为可逆矩阵,称B为A的你 矩阵。 注1可逆矩阵必是方阵。 注2A若为可逆,其逆必唯一,故A的呢矩阵记作A,即有 A4-=AA=I 注4可逆矩阵又称为非退化阵或非奇异阵或满秩阵,不可逆阵又称为退化阵或奇异阵或降 秩阵。 1.1.5可逆矩阵的性质 (1)若A可逆,则A,A均可逆,且(4=A,(A)~=(Ay PDF文件使用"pdfFactory Pro”试用版本创建,fineprint,cn
转置 ( ) ( ) ( ) ( ) T T T T T T T T T T AB B A kA kA A B A B A A = = + = + = A, B 为同维矩阵, k 为数 A的列数须等于B的行 数 1.1.3 矩阵的初等变换与初等矩阵 (1)矩阵 A 的初等变换有如下三类: 第一类:将 A 的第 i 行(列)与第 j 行(列)对换,记为 ( ) ij ij r c 。 第二类:以非零常数 k 乘 A 的 i 行(列),记作 r k (c (k )) i i ( ) 。 第三类:将 A 的第 i 行(列)的 k 倍加到第 j 行(列)上去,记作 r (k )(c (k )) ij ij 。 (2)初等矩阵是单位阵 I 经过一次初等变换后得到的矩阵 ij ij R r I ¾¾® , ( ) ( ) R k r k I i ¾¾ ® i ¾ , ( ) ( ) R k r k I ij ¾¾ij ¾® ij ij c c I ¾¾® , ( ) ( ) c k c k I i ¾¾i ¾® , ( ) ( ) R k c k I ij ¾¾ij ¾® (4) 初等变换与初等矩阵之间的关系 (5) 初等矩阵左(右)乘 A,相当与对 A 进行一次相应的初等行(列)变换,例如: B R AB r A ij ¾¾®ij Û , B AC B c A ij ij ¾¾® Û = 。 注 1 若矩阵 A 经过有限次初等变换得到矩阵 B,则称 B 与 A 等价,此时必有等式 Rs LR1AC1LCt = B 成立,其中 Rs LR1 和C1LCt 均为初等矩阵。 注 2 任一矩阵 A 经有限次初等变换后均可化为形如 ú û ù ê ë é 0 0 0 r I 的矩阵,其中 r 为 A 的秩,称 矩阵 ú û ù ê ë é 0 0 0 r I 为 A 的标准型。 1.1.4 可逆矩阵的定义 设 A 为 n 阶方阵,若存在 n 阶方阵 B,使 AB=BA=I,则称 A 为可逆矩阵,称 B 为A的你 矩阵。 注 1 可逆矩阵必是方阵。 注 2 A 若为可逆,其逆必唯一,故 A 的呢矩阵记作 -1 A ,即有 AA = A A = I -1 -1 注4 可逆矩阵又称为非退化阵或非奇异阵或满秩阵,不可逆阵又称为退化阵或奇异阵或降 秩阵。 1.1.5 可逆矩阵的性质 (1)若 A 可逆,则 T A , -1 A 均可逆,且(A ) = A - - 1 1 , ( ) T T A A 1 1 ( ) - - = PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

2)若A可递,数长0,则可地,且一 (3)若A,B是同阶可逆阵,则AB可逆,且(AB=B-A 注若A,B为同阶的可逆矩阵,则A十B不一定可逆。 1.1.6可逆矩阵的判别方法 (I)利用定义:若AB=BA=,则必有A可逆,且A=B。 (2)利用行列式:若「A≠0,则A可逆。 (3)利用性质(3):将矩阵分解成可逆矩阵的乘积。 (4)利用矩阵的秩:A为n阶方阵,若()=n,则A可逆。 (5)利用线性方程组:若n×n方程组Ar=b有唯一解,则A可逆。 (6)利用向量组的线性无关性:若方阵A的行(或列)向量线性无关,则A可逆。 (7)利用初等矩阵:若A可分解为有限个初等矩阵之积,则A可逆。 (8) 利用特 :证明数零不是A的特征值,则A可逆, (9)利用反证法:这是常用方法。 注1方法(1)在具体使用时,实际上只需验证AB=I或BA=I,即两者只要有一个成立 时,就必有A=B,当然此时A,B必须是同阶矩阵。 注2初等矩阵都是可逆阵,且其逆也是初等矩阵 (心=见风因=只得=风人小.因此,对任矩库九多存在可 逆阵P,Q,使PAQ= 「1,01 00 ,这称为A的标准分解。 注3方法(7)说明可逆阵必与单位阵等价,这一结论也是我们利用初等变换求逆矩阵的 理论依据。 1.1.7逆矩阵的计算方法 (1)利用初等变换 aI)五1合)别化】 注(1))行14)只能用行初等变换 (份列化)小只监用列脚等表换 PDF文件使用"pdfFactory Pro”试用版本创建,fineprint.cn
(2)若 A 可逆,数 k ¹ 0 ,则 kA 可逆,且 1 1 1 ( ) - - = A k kA (3) 若 A,B 是同阶可逆阵,则 AB 可逆,且( ) -1 -1 -1 AB = B A 注 若 A,B 为同阶的可逆矩阵,则 A+B 不一定可逆。 1.1.6 可逆矩阵的判别方法 (1) 利用定义:若 AB=BA=I,则必有 A 可逆,且 A = B -1 。 (2) 利用行列式:若 éAù ¹ 0,则 A 可逆。 (3) 利用性质(3):将矩阵分解成可逆矩阵的乘积。 (4) 利用矩阵的秩:A 为 n 阶方阵,若 r(A) = n,则 A 可逆。 (5) 利用线性方程组:若 n´ n 方程组 Ax = b 有唯一解,则 A 可逆。 (6) 利用向量组的线性无关性:若方阵 A 的行(或列)向量线性无关,则 A 可逆。 (7) 利用初等矩阵:若 A 可分解为有限个初等矩阵之积,则 A 可逆。 (8) 利用特征值:证明数零不是 A 的特征值,则 A 可逆。 (9) 利用反证法:这是常用方法。 注1 方法(1)在具体使用时,实际上只需验证 AB=I 或 BA=I,即两者只要有一个成立 时,就必有 A = B -1 ,当然此时 A,B 必须是同阶矩阵。 注2 初 等 矩 阵 都 是 可 逆 阵 , 且 其 逆 也 是 初 等 矩 阵 ( ( ) R ( ) k R ( k ) k Rij Rij Ri k Ri ÷ ij = ij - ø ö ç è æ = = -1 -1 -1 , 1 , ),因此,对任一矩阵 A,必存在可 逆阵 P,Q,使 ú û ù ê ë é = 0 0 0 r I PAQ ,这称为 A 的标准分解。 注3 方法(7)说明可逆阵必与单位阵等价,这一结论也是我们利用初等变换求逆矩阵的 理论依据。 1.1.7 逆矩阵的计算方法 (1) 利用初等变换 ( ) ( ) 1 | | 行 - A I ¾¾® I A 或 ÷ ÷ ø ö ç ç è æ ÷ ÷ ¾¾® ø ö ç ç è æ 1 I A - 列 A I 注 ( ) ( ) 1 | | 行 - A I ¾¾® I A 只能用行初等变换 ÷ ÷ ø ö ç ç è æ ÷ ÷ ¾¾® ø ö ç ç è æ 1 I A - 列 A I 只能用列初等变换 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn

(2)利用伴随阵 注在具体计算时这一公式适用于较低阶的矩阵 (3)利用分块矩阵 (4)凑法:当条件中有矩阵方程时,通过矩阵运算规律从矩阵方程中凑出AB=I的形式, 从而可得A=B,这一方法适用于抽象矩阵求逆。 1.1.8分块矩阵的定义于运算 (1)定义 用若干条纵线和横线把一个矩阵分成若干个小块。每一小块称为矩阵的一个子块和 子矩阵,则一这些子块为元素的原矩阵称为分块矩阵, (2)运算 (3)进行分块矩阵的加、减、乘法和转置运算,可降子矩阵当作通常矩阵的元素看待。 注1同维矩阵,只有用同样的分块方法时,才能进行分块相加。 这2分块乘法只有当左边矩阵分法于右边矩阵的行分法一致时才能进行。 注4分块转置除了行列互换外,每一子块也需转置,即若 AA2…A 4=4…4, ::: AA2…An 则 「AA…A 4T= A站A品…A AA…A 1.1.9利用分块矩阵求逆矩阵 (1)对分块对角阵 A 若A,=1,2,…,s)可逆,则A可逆且 PDF文件使用"pdfFactory Pro”试用版本创建,fineprint,cn
(2) 利用伴随阵 A A A * 1 = - 注 在具体计算时这一公式适用于较低阶的矩阵 (3) 利用分块矩阵 (4) 凑法:当条件中有矩阵方程时,通过矩阵运算规律从矩阵方程中凑出 AB=I 的形式, 从而可得 A = B -1 ,这一方法适用于抽象矩阵求逆。 1.1.8 分块矩阵的定义于运算 (1) 定义 用若干条纵线和横线把一个矩阵分成若干个小块。每一小块称为矩阵的一个子块和 子矩阵,则一这些子块为元素的原矩阵称为分块矩阵。 (2) 运算 (3) 进行分块矩阵的加、减、乘法和转置运算,可降子矩阵当作通常矩阵的元素看待。 注 1 同维矩阵,只有用同样的分块方法时,才能进行分块相加。 这 2 分块乘法只有当左边矩阵分法于右边矩阵的行分法一致时才能进行。 注4 分块转置除了行列互换外,每一子块也需转置,即若 ú ú ú ú û ù ê ê ê ê ë é = s s sr r r A A A A A A A A A A L M M M L L 1 2 21 22 2 11 12 1 则 ú ú ú ú ú û ù ê ê ê ê ê ë é = T sr T r T r T s T T T s T T T A A A A A A A A A A L M M M L L 1 2 12 22 2 11 21 1 1.1.9 利用分块矩阵求逆矩阵 (1) 对分块对角阵 ú ú ú ú û ù ê ê ê ê ë é = As A A A O 2 1 若 Ai (i = 1,2,L,s)可逆,则 A 可逆且 PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn
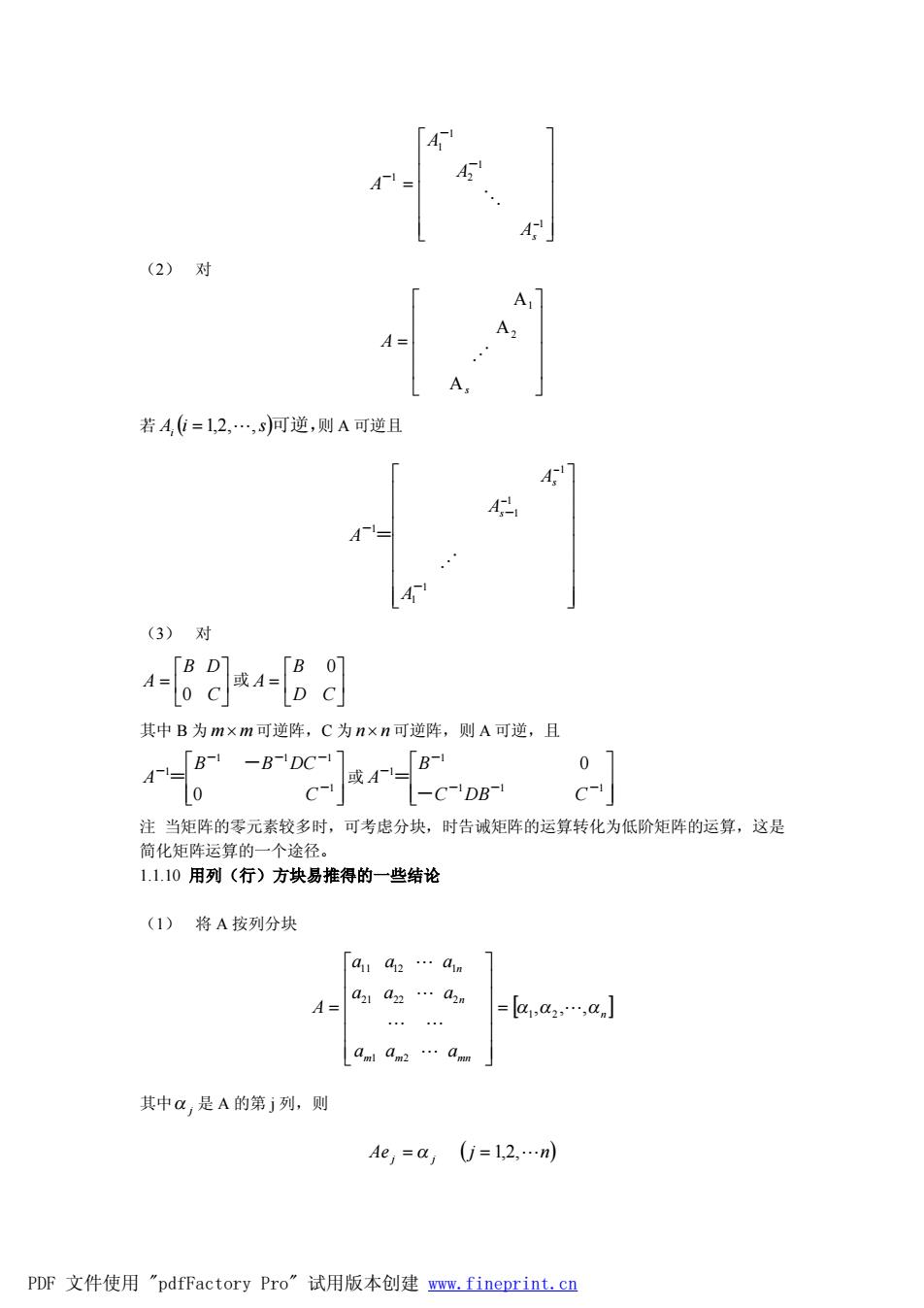
(2)对 A 若A,=1,2,,s)可逆,则A可逆且 A (3)对 4 D C 其中B为m×m可逆阵,C为n×n可逆阵,则A可逆,且 哦4 07 o C L-C-DB C 注当矩阵的零元素较多时,可考虑分块,时告诚矩阵的运算转化为低阶矩阵的运算,这是 简化矩阵运算的一个途径。 1.1.10用列(行)方块易推得的一些结论 (1)将A按列分块 a1a2…am A= a1am…an =a,a2,…,an] dd2…am 其中a,是A的第j列,则 Ae,=a,U=1,2,…nm PDF文件使用"pdfFactory Pro”试用版本创建,fineprint.cn
ú ú ú ú ú û ù ê ê ê ê ê ë é = -1 1 2 1 1 1 As A A A O - - - (2) 对 ú ú ú ú û ù ê ê ê ê ë é = s A A A A 2 1 N 若 Ai (i = 1,2,L,s)可逆,则 A 可逆且 ú ú ú ú ú ú ú û ù ê ê ê ê ê ê ê ë é - - 1 1 1 1 1 1 - - - = A A A A s s N (3) 对 ú û ù ê ë é = C B D A 0 或 ú û ù ê ë é = D C B A 0 其中 B 为 m´ m可逆阵,C 为 n´ n 可逆阵,则 A 可逆,且 ú ú û ù ê ê ë é 1 1 1 1 1 0 - - - - - - = C B B DC A 或 ú ú û ù ê ê ë é 1 1 1 1 1 0 - - - - - - = C DB C B A 注 当矩阵的零元素较多时,可考虑分块,时告诫矩阵的运算转化为低阶矩阵的运算,这是 简化矩阵运算的一个途径。 1.1.10 用列(行)方块易推得的一些结论 (1) 将 A 按列分块 [ ] n m m mn n n a a a a a a a a a A a1 ,a2 , ,a 1 2 21 22 2 11 12 1 L L L L L L = ú ú ú ú ú û ù ê ê ê ê ê ë é = 其中a j 是 A 的第 j 列,则 Ae ( j n) j = a j = 1,2,L PDF 文件使用 "pdfFactory Pro" 试用版本创建 www.fineprint.cn