
反三角函数 1.反正弦函数 定义1把正弦函数y=sinx,x∈[-,]的反函数 叫做反正弦函数,记作y=arcsinx或y=sin1x. (1)定义域D=[-1,1] (2)值域M=[-271 (3)公式sin(arcsin x)=x,x∈[-1,1] arcsin(-x)=-arcsinx ,x E [-1,1]
反三角函数 1.反正弦函数
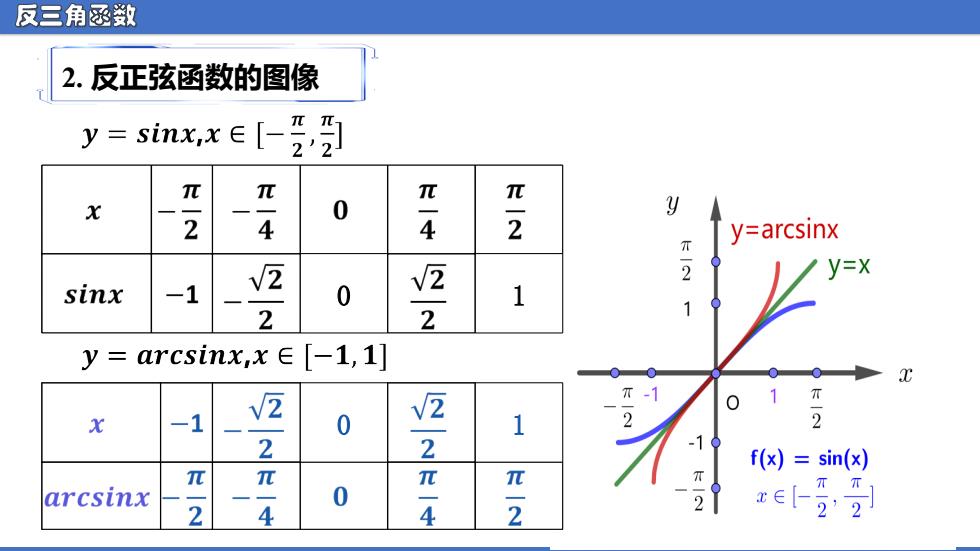
反三角函数 2.反正弦函数的图像 y=sinx.xe[ π π X 2 0 4 4 y y=arcsinx 2 y=X sinx -1 √2 0 2 1 2 y=arcsinx,x∈[-1,1] V2 π-1 0 1 X -1 0 √2 1 2 2 2 -1 f(x)=sin(x) 元 π π π arcsinx 0 2 4 4 2 2 22
反三角函数 2. 反正弦函数的图像 0 1 0 1