
平稳随机信号自相关函数特性(l) 对称性R[n]=R,[-n]R,[n]=R[-n](2)极限值n=0R,[O]=E(X[k]n>80R[]=m?(3)不等式R.[O]≥R,[n]
平稳随机信号自相关函数特性 (1)对称性 R [n] R [ n] x = x − [ ] [ ] * Rx n = Rx −n (2)极限值 n = 0 [0] { [ ]} 2 R E X k x = n→ 2 [ ] Rx = mx (3)不等式 R [0] R [n] x x

2.各态遍历随机信号集平均等于时间平均≥√x[k]mx = E(X[k]}) = limN-→ 2N +1K=-NN工E[x[k]-m,]?= E([X[k]-m]= limN-→ 2N + 1=-NNZR[n]== E(X[k]X[k +n]) = lim x[k]x[k +n] N→ 2N +1=-N
2. 各态遍历随机信号 集平均等于时间平均 =− → + = = N k N N x x k N m E X k [ ] 2 1 1 { [ ]} lim =− → − + = − = N k N x N x x x k m N E X k m 2 2 2 [ [ ] ] 2 1 1 {[ [ ] ] } lim [ ] [ ] 2 1 1 [ ] { [ ] [ ]} lim x k x k n N R n E X k X k n N k N N x + + == + = =− →
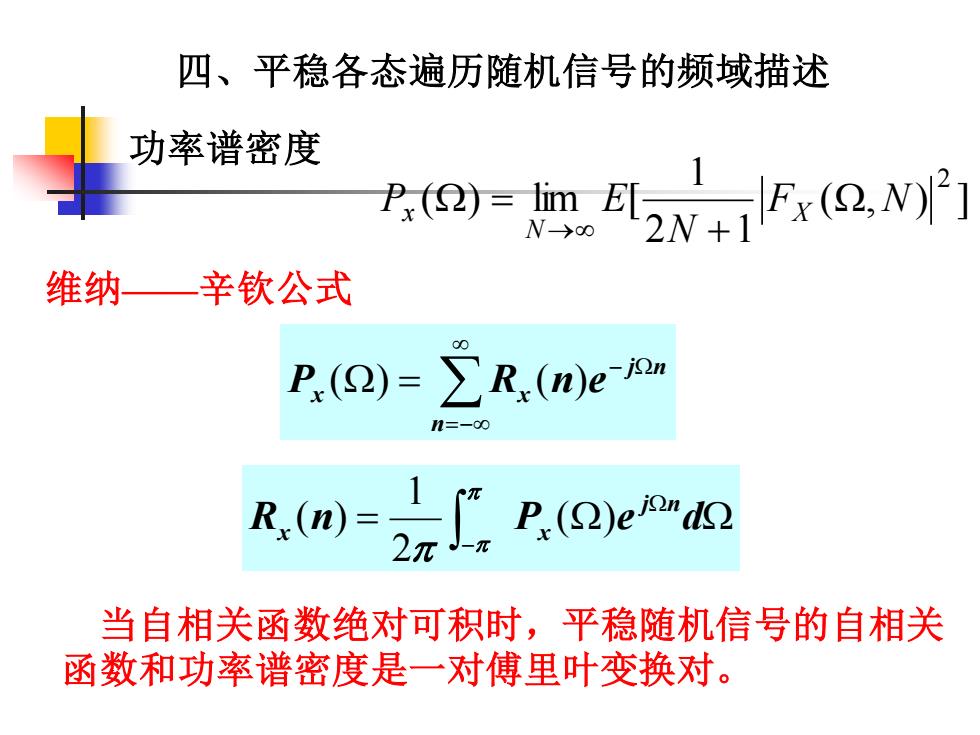
四、平稳各态遍历随机信号的频域描述功率谱密度x (2, N)2]EIP (2) = lim2N+1N->8维纳—辛钦公式R,(n)e-jonZP,(2) =n=-8024P (2)ejandQR.(n)2元-元当自相关函数绝对可积时,平稳随机信号的自相关函数和功率谱密度是一对傅里叶变换对
四、平稳各态遍历随机信号的频域描述 维纳——辛钦公式 =− − = n j n x x P ( ) R (n)e = − R n P e d j n x x ( ) 2 1 ( ) ( , ) ] 2 1 1 ( ) lim [ 2 F N N P E X N x + = → 当自相关函数绝对可积时,平稳随机信号的自相关 函数和功率谱密度是一对傅里叶变换对。 功率谱密度

平稳随机序列通过LTI离散时间系统输出序列的均值输出序列的自相关函数输出序列的功率谱输入/输出序列的互相关函数及互功率谱
平稳随机序列通过LTI离散时间系统 ◼ 输出序列的均值 ◼ 输出序列的自相关函数 ◼ 输出序列的功率谱 ◼ 输入/输出序列的互相关函数及互功率谱
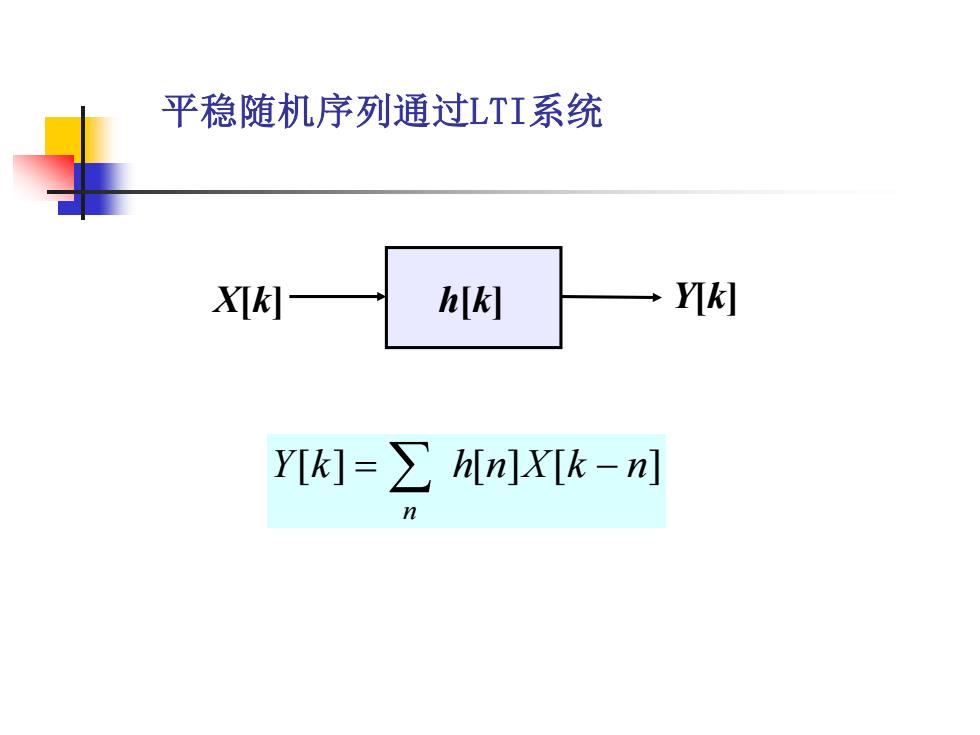
平稳随机序列通过LTI系统-Y[K]X[k]h[k]Y[k] =h[n]X[k -n]n
平稳随机序列通过LTI系统 X[k] h[k] Y[k] Y[k] h[n]X[k n] n = −