复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 表2-2几种抑制分数杂散的方法 分数杂散抑制技术 优点 缺点 DAC补偿可 用DAC的方法抑制杂散 模拟电路要精确匹配 随机数注入阿 随机化分频器的控制信号 频率上存在抖动,会引 入低频噪声 相位内差可 利用压控振荡器输出的多 模拟电路要精确匹配 相位性 sigma--delta噪声整型8 利用sigma-delta调制器的 高频处引入量化噪声 噪声整型特性 (1)DAC补偿方法:图2.5和图2.6分别描述了采用DAC补偿的系统框图和 波型图。DAC输出的电流信号和电荷泵输出的电流信号进行代数求和后再注入 到环路滤波器。如果锁定时电荷泵输出电流和DAC输出电流完全匹配的话,就 可以彻底的抑制分数杂散。但由于DAC的分辨率和精度有限,DAC产生的电流 和电荷泵输出的电流不可能精确匹配。因此采用这种方法最好也只能够把 fractional spur做到-6OdBc/Hz,这不能满足性能指标要求。 fref PFD+CP Loop Filter /CO u=(N+m/2)frer N/N+1 DAC Carry Tref k-bit ACCUM m 图2.5采用DAC补偿的分数分频频率综合器系统框图 6UUUUL fdiv 中aiw中ref Vctrt-cp Vctr-DAC Vetr 图2.6采用DAC补偿的分数分频频率综合器具体工作波型 】
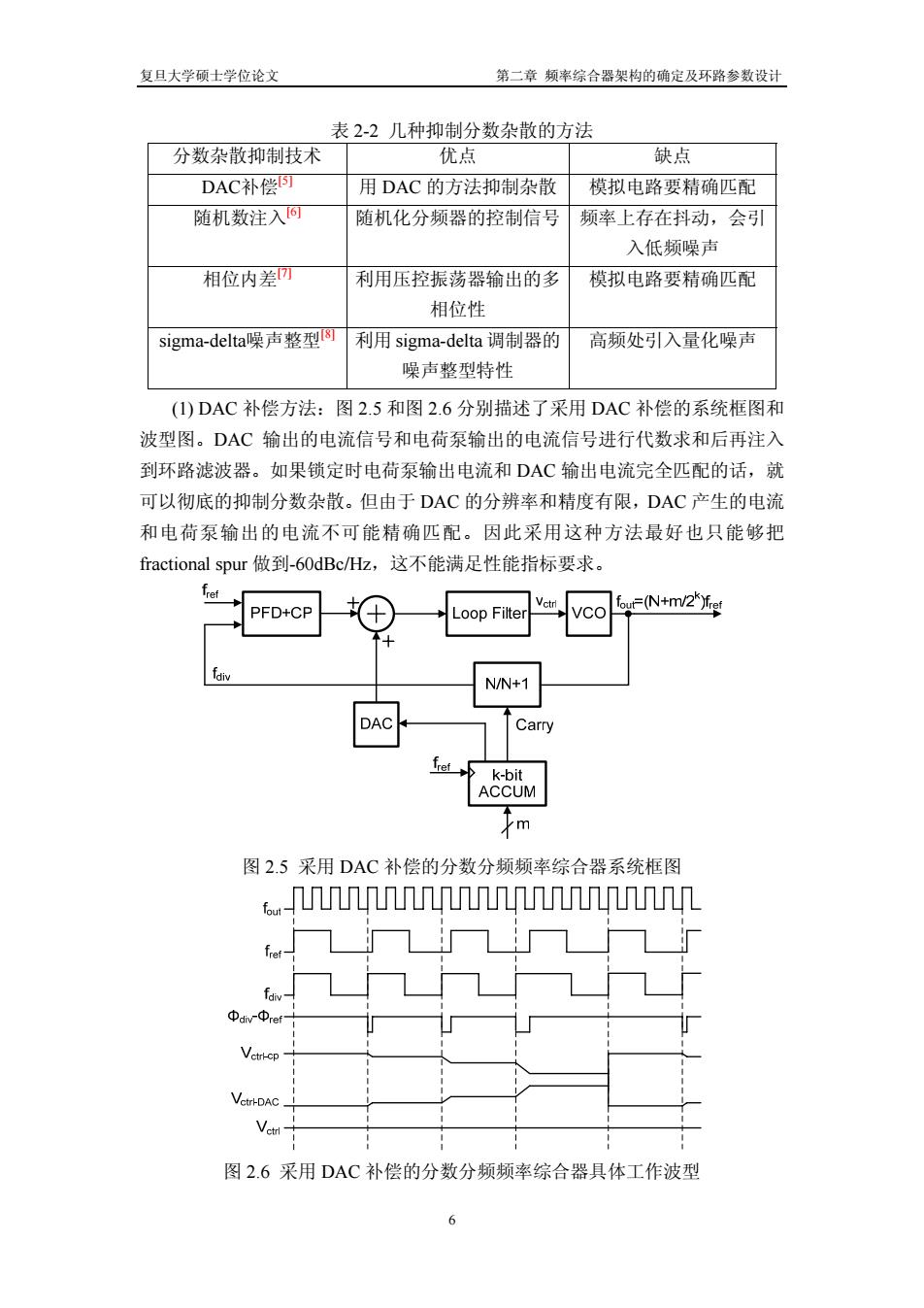
复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 表 2-2 几种抑制分数杂散的方法 分数杂散抑制技术 优点 缺点 DAC补偿[5] 用 DAC 的方法抑制杂散 模拟电路要精确匹配 随机数注入[6] 随机化分频器的控制信号 频率上存在抖动,会引 入低频噪声 相位内差[7] 利用压控振荡器输出的多 相位性 模拟电路要精确匹配 sigma-delta噪声整型[8] 利用 sigma-delta 调制器的 噪声整型特性 高频处引入量化噪声 (1) DAC 补偿方法:图 2.5 和图 2.6 分别描述了采用 DAC 补偿的系统框图和 波型图。DAC 输出的电流信号和电荷泵输出的电流信号进行代数求和后再注入 到环路滤波器。如果锁定时电荷泵输出电流和 DAC 输出电流完全匹配的话,就 可以彻底的抑制分数杂散。但由于 DAC 的分辨率和精度有限,DAC 产生的电流 和电荷泵输出的电流不可能精确匹配。因此采用这种方法最好也只能够把 fractional spur 做到-60dBc/Hz,这不能满足性能指标要求。 图 2.5 采用 DAC 补偿的分数分频频率综合器系统框图 图 2.6 采用 DAC 补偿的分数分频频率综合器具体工作波型 6
复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 (2)随机数注入的方法:分数杂散产生的原理就是双模分频器控制信号的时 序呈周期性,因此如果把一个随机数发生器的输出注入到分频器的控制端,同样 可以抑制分数杂散。图2.7给出了带随机数发生器的分数分频频率综合器的框图, 对于分频器的每一个输出,随机数发生器都会输出一个新的随机数P,P和频率 控制字K的比较值用于决定分频比是N还是N+1。因为K控制双模分频器的模数, 它的平均值就是需要的分数分频比。实际上,随机数就是白噪声(white noise),频 率域上的白噪声会转化为相位域上的1P噪声,这是不会被环路抑制掉的,因此 频率综合器的低频噪声性能会被1/P噪声恶化。 PFD+CP Loop Filter /Co fout Tdiv N/N+1 N-bit word comparator 和 Random number generator 图2.7带随机数发生器的分数分频频率综合器的系统框图 PFD-CP 4-stage Loop filter ring oscillator Phase interpolator Frequency control 图2.8基于VCO相位内插法的分数分频频率综合器的系统框图 (3)VCO相位内插法:一般来说,N级的环型振荡器会产生N个不同的相位, 当我们需要某一个分数分频比时只需从中选择一个正确的相位即可。然而对于射 频VCO来说,反相器的级数不可能很多,这样就必须使用相位内差器(phase 7
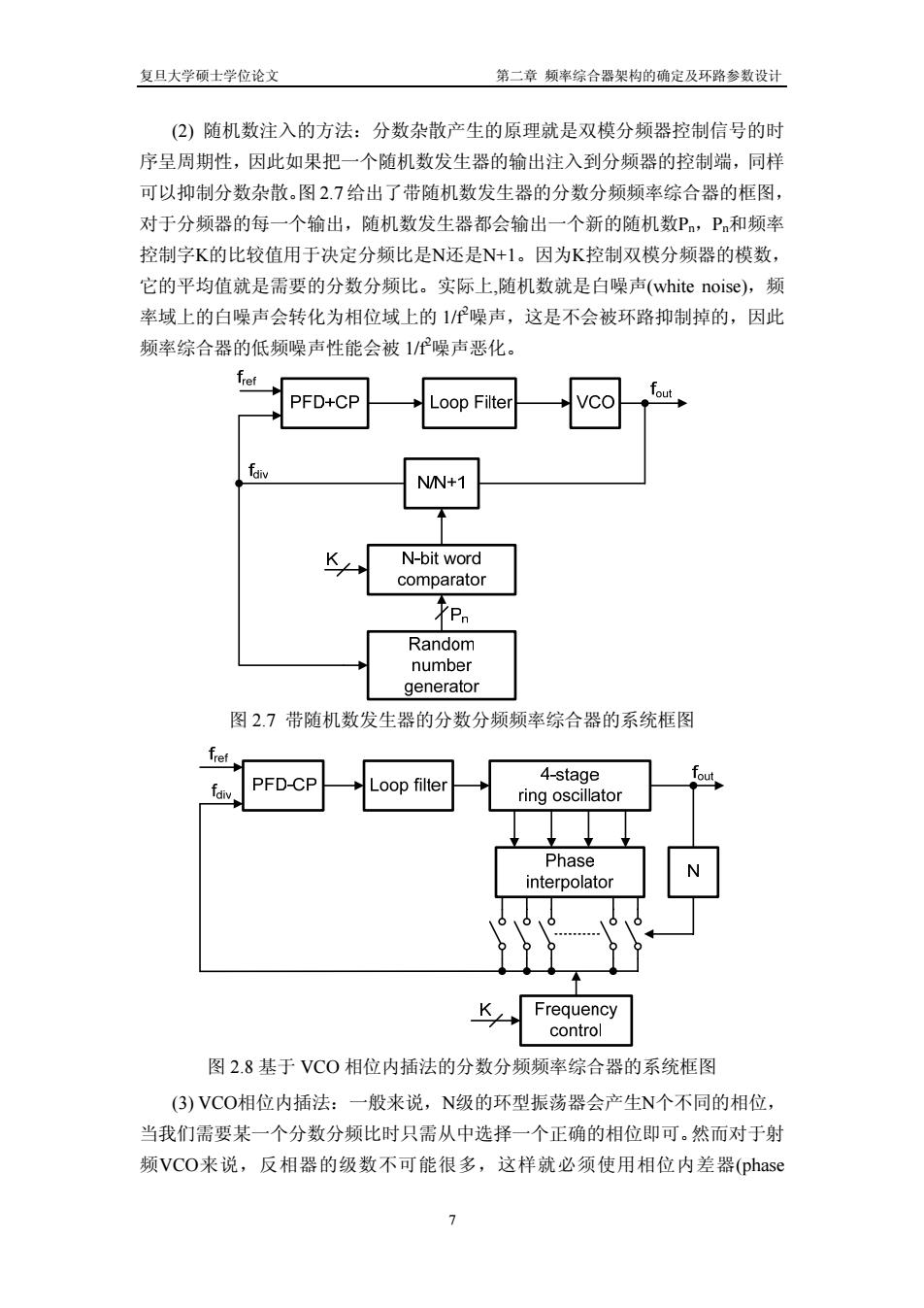
复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 (2) 随机数注入的方法:分数杂散产生的原理就是双模分频器控制信号的时 序呈周期性,因此如果把一个随机数发生器的输出注入到分频器的控制端,同样 可以抑制分数杂散。图 2.7 给出了带随机数发生器的分数分频频率综合器的框图, 对于分频器的每一个输出,随机数发生器都会输出一个新的随机数Pn,Pn和频率 控制字K的比较值用于决定分频比是N还是N+1。因为K控制双模分频器的模数, 它的平均值就是需要的分数分频比。实际上,随机数就是白噪声(white noise),频 率域上的白噪声会转化为相位域上的 1/f2 噪声,这是不会被环路抑制掉的,因此 频率综合器的低频噪声性能会被 1/f2 噪声恶化。 图 2.7 带随机数发生器的分数分频频率综合器的系统框图 图 2.8 基于 VCO 相位内插法的分数分频频率综合器的系统框图 (3) VCO相位内插法:一般来说,N级的环型振荡器会产生N个不同的相位, 当我们需要某一个分数分频比时只需从中选择一个正确的相位即可。然而对于射 频VCO来说,反相器的级数不可能很多,这样就必须使用相位内差器(phase 7
复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 interpolator)9来产生足够多的相位,实现分数分频时只需从内插得到的相位里选 择一个正确的即可。图2.8即为采用VCO相位内插法来抑制分数杂散的系统框图。 由于实际上选择的是相位信号的上升或下降沿,任何沿之间的时间偏差都会引入 杂散,因此这种抑制杂散的方法也是极大的依赖模拟电路的匹配程度,不太适宜 实际应用。 (4)基于sigma-delta噪声整型的抑制杂散的方法:这是目前比较流行的一种 抑制杂散的方法。因为二阶或更高阶数的sigma-delta调制器对于直流输入是不 会产生fixed tones的,所以基于sigma-delta噪声整型的方法是可以很好的抑制分 数杂散能量的。调制器结构是数字实现,可以完全避免模拟电路失配性的影响。 同时锁相环路自身的低通特性还可以完全滤除由于噪声整型而转移到高频处的 噪声。图2.9是基于sigma-delta噪声整型的分数分频频率综合器的系统架构。因 为sigma-delta噪声整型的方法可以有效的降低分数杂散,同时避免了模拟电路 的失配影响,所以设计中将选择sigma-delta结构的分数分频频率综合器结构。 PFD-CP _oop-filter /CO o N/N+1 △-Σ modulator 图2.9基于sigma-delta噪声整型的的分数分频频率综合器系统架构 2.3频率综合器的环路参数设计 频率综合器设计的一个重要环节就是环路参数的设计,参数设计的好坏直接 决定着频率综合器的整体性能。本设计中采用四阶锁相环路来抑制三阶 sigma-delta调制器所产生的高频噪声。一般来说,分析四阶环路最常用的的方法 是相位裕度最大法o-I川,但它不能定量反映PVT(Process Voltage Temperature)的 变化对环路参数的影响。本节为了优化环路系统的稳定性,设计中首先对四阶环 路进行了合理近似,分析表明所做近似不会改变系统的开环和闭环特性,然后对 四阶系统进行了基于稳定性优化的环路参数设计,最后本章还总结了频率综合 器的环路参数设计流程
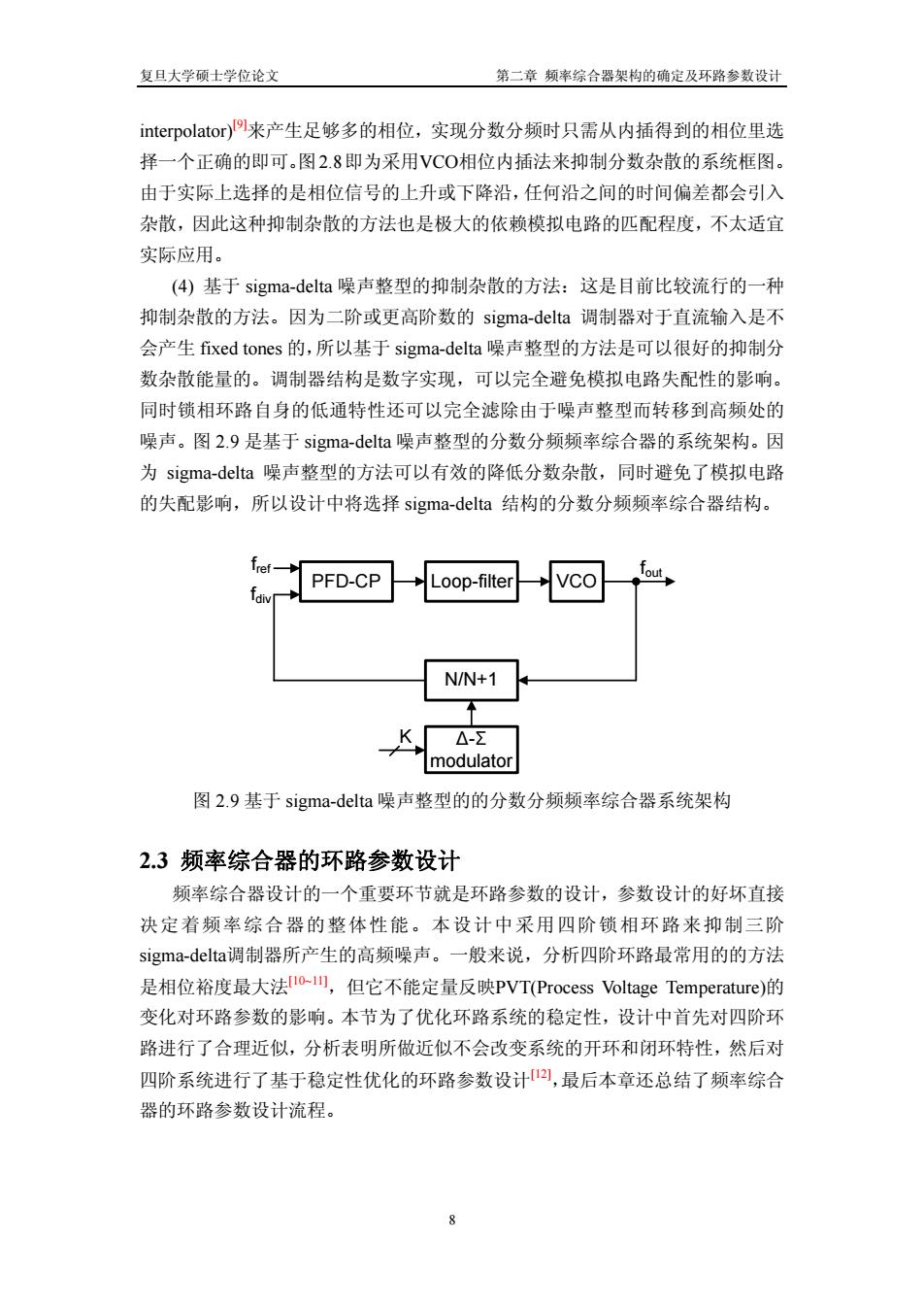
复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 interpolator)[9]来产生足够多的相位,实现分数分频时只需从内插得到的相位里选 择一个正确的即可。图2.8即为采用VCO相位内插法来抑制分数杂散的系统框图。 由于实际上选择的是相位信号的上升或下降沿,任何沿之间的时间偏差都会引入 杂散,因此这种抑制杂散的方法也是极大的依赖模拟电路的匹配程度,不太适宜 实际应用。 (4) 基于 sigma-delta 噪声整型的抑制杂散的方法:这是目前比较流行的一种 抑制杂散的方法。因为二阶或更高阶数的 sigma-delta 调制器对于直流输入是不 会产生 fixed tones 的,所以基于 sigma-delta 噪声整型的方法是可以很好的抑制分 数杂散能量的。调制器结构是数字实现,可以完全避免模拟电路失配性的影响。 同时锁相环路自身的低通特性还可以完全滤除由于噪声整型而转移到高频处的 噪声。图 2.9 是基于 sigma-delta 噪声整型的分数分频频率综合器的系统架构。因 为 sigma-delta 噪声整型的方法可以有效的降低分数杂散,同时避免了模拟电路 的失配影响,所以设计中将选择 sigma-delta 结构的分数分频频率综合器结构。 PFD-CP Loop-filter VCO N/N+1 Δ-Σ modulator K fref fout fdiv 图 2.9 基于 sigma-delta 噪声整型的的分数分频频率综合器系统架构 2.3 频率综合器的环路参数设计 频率综合器设计的一个重要环节就是环路参数的设计,参数设计的好坏直接 决定着频率综合器的整体性能。本设计中采用四阶锁相环路来抑制三阶 sigma-delta调制器所产生的高频噪声。一般来说,分析四阶环路最常用的的方法 是相位裕度最大法[10~11],但它不能定量反映PVT(Process Voltage Temperature)的 变化对环路参数的影响。本节为了优化环路系统的稳定性,设计中首先对四阶环 路进行了合理近似,分析表明所做近似不会改变系统的开环和闭环特性,然后对 四阶系统进行了基于稳定性优化的环路参数设计[12],最后本章还总结了频率综合 器的环路参数设计流程。 8
复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 2.3.1闭环三阶s域模型 cp Z-(s) 中in(s) 中oui(s) PFD+CP Loop Filter 中av(s)=中ou(s)/N Divider N 图2.10三阶频率综合器的s域线性模型 三阶频率综合器的s域模型如图2.10所示,Ip为电荷泵(CP)的电流,Z(S)为 环路滤波器(Loop Filter)的传递函数,Kvco为压控振荡器(VCO)的增益,N为分频 器(Divider)的分频比。开环传递函数为: H.()=2Z,.Kw (2-1) 2π·N cp Vctrl 图2.11无源二阶环路滤波器 其中,环路滤波器为二阶无源电阻电容网络(图2.11),其传递函数为: 1 S+- Z(s)= 1+sRC 1 RC 1S+0 3(C+C:+sRCC:)C:s(s+- (2-2) 1 CC C2s(s+0p2) C,+C2 其中的ozop1、o2分别是环路滤波器的零点和极点,具体表示为: 1 0.= RG0n=0;0: C,+C2 (2-3) RCC2 因此三阶锁相环路的s域开环传递函数为: H(s)= IcpKyco.s+o (2-4) 2πC,NS2(s+02)
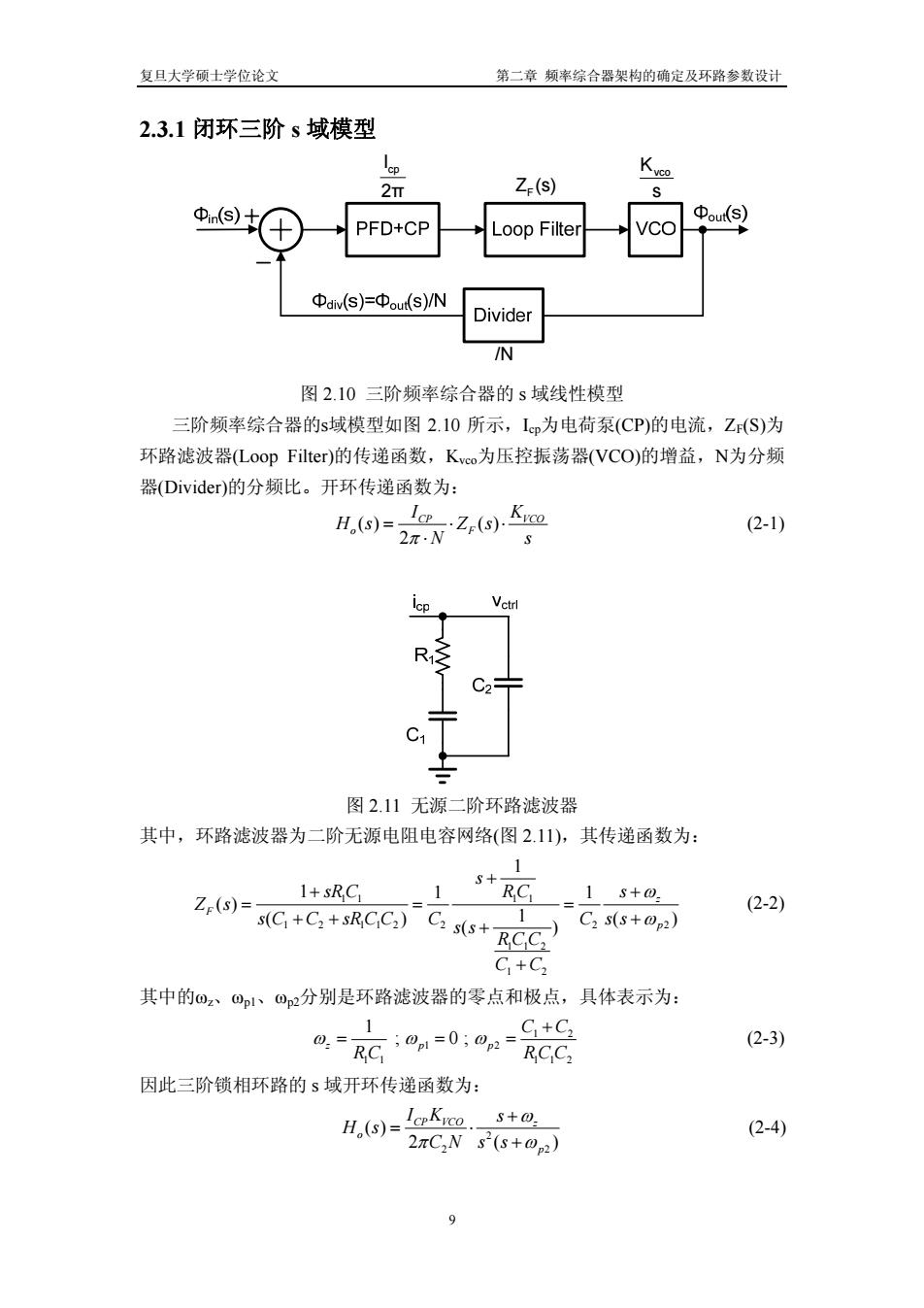
复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 2.3.1 闭环三阶 s 域模型 cp I 2π Z (s) F Kvco s /N 图 2.10 三阶频率综合器的 s 域线性模型 三阶频率综合器的s域模型如图 2.10 所示,Icp为电荷泵(CP)的电流,ZF(S)为 环路滤波器(Loop Filter)的传递函数,Kvco为压控振荡器(VCO)的增益,N为分频 器(Divider)的分频比。开环传递函数为: () () 2 CP VCO o F I Hs Z s π N s = ⋅⋅ ⋅ K (2-1) 图 2.11 无源二阶环路滤波器 其中,环路滤波器为二阶无源电阻电容网络(图 2.11),其传递函数为: 1 1 1 1 1 2 112 2 2 2 112 1 2 1 1 1 1 ( ) () ( 1 ( ) z F p s sR C R C s Z s s C C sR C C C C ss s s RCC C C ω ω + + + = == + + + + + ) (2-2) 其中的ωz、ωp1、ωp2分别是环路滤波器的零点和极点,具体表示为: 1 1 2 1 1 112 1 ; 0 ; z pp C C2 R C R ω ωω C C + = == (2-3) 因此三阶锁相环路的 s 域开环传递函数为: 2 2 2 ( ) 2 ( CP VCO z o p I K s H s CN s s ) ω π ω + = ⋅ + (2-4) 9

复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 其中K='K巴为环路增益。 2πC,N 由此闭环传递函数的表达式为: H(s)= NH。(s) NK(s+@.) (2-5) +H。(s)s3+⊙2s2+Ks+K0 三阶锁相环系统的闭环传递函数也可以写成: H(S)= NK(s+@) (2-6) (s2+250n3+o1)s+0p) 对比(2-5)、(2-6)式可以得到开环参数(K,oz,op2)和闭环参数(G,0n,op)之间的关系 如下: 250n+0p=0p2 0i+250n0p=K' (2-7) @@p=K'0. 可得: 0n=m(b,5)×0 (2-8) 0p=(b+1-25×m(b,5)》×0 (2-9) K'=IcnKrco=k(b.5)x (2-10) 2πC,N 其中,m(b,)和k(b,)分别由下列两式解出 25m2(b,5)-(452+b)m(b,5)+25(b+1)=0 (2-11) k(b,5)=(1-452)m2+25(b+1)m (2-12) 因此,只要确定电容比b和系统的衰减因子℃的值,就可以确定(b,)和k(b,): 再根据(2-8)(2-10)式,就可以由开环参数确定闭环参数,从而用根轨迹的方法直 接对闭环系统精确分析,避免了用开环分析来近似,可以精确的定量描述环路参 数变化与稳定性之间的关系。 对于频率综合器而言,不同的输出频率对应着不同的分频比N。同时由于压 控振荡器的调频带分为多根,中心频率越低的带,其固定电容越大,所对应的 VCO增益就越低,因此不同的输出频率对应着不同的压控增益Kvco同时在CMOS 集成电路中,频率综合器的很多参数和变量都将随着工艺、电压和温度PVT)的 改变而变化,因此在环路参数设计时必须考虑一定的裕量。常用的相位裕度最大 法是基于开环分析的,相位裕度的取值多少不能和PVT的变化直接联系起来,而 且相位裕度最大法也不能定量的反映由于PVT所引起的参数变化对实际环路的 影响。 10
复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 其中 ' 2 2 CP VCO I K K πC N = 为环路增益。 由此闭环传递函数的表达式为: ' 3 2' ' 2 ( ) ( ) ( ) 1 () o z o p NH s NK s H s H s s s Ks K ω ω ωz + = = + + ++ (2-5) 三阶锁相环系统的闭环传递函数也可以写成: ' 2 2 ( ) ( ) ( 2 )( z n n NK s H s s ss ω ) p ζωω ω + = + ++ (2-6) 对比(2-5)、(2-6)式可以得到开环参数(K’ , ωz, ωp2)和闭环参数(ζ, ωn, ωp)之间的关系 如下: 2 2 2 2 2 ' ' np p n np np z K K ζωω ω ω ζω ω ωω ω + = + = = z (2-7) 可得: ωn = m b(, ) ζ ×ω (2-8) 1 2 p b mb ω z =+ × × ( - ( , )) ζ ζ ω (2-9) 2 2 2 CP VCO z I K K k b C N ζ ω π ' ( = = , )× 1 0 (2-10) 其中,m(b, ζ)和 k(b, ζ)分别由下列两式解出 2 2 24 2 ζ ζ ζ ζζ m b bmb b (, ) ( ) (, ) ( ) − + + += (2-11) 2 2 k b(, ) ( ) ( ) ζζζ =− + + 14 2 1 m b m (2-12) 因此,只要确定电容比 b 和系统的衰减因子 ζ 的值,就可以确定 m(b, ζ)和 k(b, ζ); 再根据(2-8)~(2-10)式,就可以由开环参数确定闭环参数,从而用根轨迹的方法直 接对闭环系统精确分析,避免了用开环分析来近似,可以精确的定量描述环路参 数变化与稳定性之间的关系。 对于频率综合器而言,不同的输出频率对应着不同的分频比N。同时由于压 控振荡器的调频带分为多根,中心频率越低的带,其固定电容越大,所对应的 VCO增益就越低,因此不同的输出频率对应着不同的压控增益Kvco。同时在CMOS 集成电路中,频率综合器的很多参数和变量都将随着工艺、电压和温度(PVT)的 改变而变化,因此在环路参数设计时必须考虑一定的裕量。常用的相位裕度最大 法是基于开环分析的,相位裕度的取值多少不能和PVT的变化直接联系起来,而 且相位裕度最大法也不能定量的反映由于PVT所引起的参数变化对实际环路的 影响。 10