复旦大学：《微电子学与固体电子学》教学资源（硕士士学位论文）频率综合器相位噪声分析及全差分电荷泵设计 Analysis of Phase Noise in Frequency Synthesizer and Fully-Differential Charge Pump Design

复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 +unstable locus for poles 45 × open loop poles ▣ closed loop poles zeros 兴 Wp2 8, 45 图2.12三阶闭环系统的根轨迹 那么如何来定量分析上述的各种变化对环路稳定性的影响呢？由图2.12所 示的三阶闭环系统的根轨迹图可知稳定边界的阻尼因子（是0.707，所以需要知 道g由设计值Cop变化到gb对应着多少PVT和N的变化。由(2-1O)式可以得到kp和环 路参数的关系式是： kop =k(bap Som)= Ko·lp·bR2.C (2-13) 2πN 令α为变化因子，用来表示实际环路参数(Kvco,Icp,b,R1,C1,N)的变化所引起的k(b, C)的变化，min和amax的定义式分别如下： knmn(bpr,So） k(bprop (2-14) kmax(bpm,S6） dmax= k(opop) 变化因子的最优值aopt的定义式为： a&gpt=Vamin·amax (2-15) 对于任何一种CMOS工艺，可以通过查阅工艺文件以及估算Ko、Ip和N的变 化量来计算出实际工艺所能达到的Cmin和amax,这里重新定义为amin-p和amax-P。如 果(amin-P,amax-p)在选取的(bopt,Cop)值所对应的(amin,amax)范围之内，就无需采用 任何补偿措施，只要PVT满足工艺文件所描述的范围，系统就一定会稳定。如果 (amin-P,amax-P)超出(amin,Cmax)的范围，就必须采取补偿措施来扩大amim和amax的范 11

复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 45° 45° unstable ωp2 ωz 0 locus for poles open loop poles closed loop poles zeros 图 2.12 三阶闭环系统的根轨迹 那么如何来定量分析上述的各种变化对环路稳定性的影响呢？由图 2.12 所 示的三阶闭环系统的根轨迹图可知稳定边界的阻尼因子ζb是 0.707，所以需要知 道ζ由设计值ζopt变化到ζb对应着多少PVT和N的变化。由(2-10)式可以得到kopt和环 路参数的关系式是： 2 1 2 (, ) ζ π 1 ⋅ ⋅⋅ ⋅ = = vco cp opt opt opt K I bR C k kb N (2-13) 令α为变化因子，用来表示实际环路参数(Kvco, Icp, b, R1, C1, N)的变化所引起的k(b, ζ)的变化，αmin和αmax的定义式分别如下： opt b opt opt opt b opt opt k b k b k b k b ζ α ζ ζ α ζ = = min min max max ( ,) (, ) ( , (, ) ) (2-14) 变化因子的最优值αopt的定义式为： α αα opt = ⋅ min max (2-15) 对于任何一种CMOS工艺，可以通过查阅工艺文件以及估算Kvco、Icp和N的变 化量来计算出实际工艺所能达到的αmin和αmax，这里重新定义为αmin－P和αmax－P。如 果(αmin－P,αmax－P)在选取的(bopt, ζopt)值所对应的(αmin，αmax)范围之内，就无需采用 任何补偿措施，只要PVT满足工艺文件所描述的范围，系统就一定会稳定。如果 (αmin－P,αmax－P)超出(αmin，αmax)的范围，就必须采取补偿措施来扩大αmin和αmax的范 11

复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 围。其中最有效的方法就是加倍或减半电荷泵的电流以使(2-14)中amin和amax的分 母减小或增加。表2-3给出了b、Copt、amim和amax几个量之间的数值关系。可以看 到，随着电容比b的增加，最优的阻尼因子Co也在增加，并且变化裕量也在增加， 也就是说环路更加稳定。 表2-3电容比与最优阻尼因子、最优变化因子、边界变化因子关系表 电容比b 9 10 12 20 opt 1.0119 1.0311 1.0766 1.2702 Lopt 1.0201 1.0388 1.073 1.1814 C.max 1.5548 1.637 1.7878 2.2855 Amin 0.6431 0.6109 0.5594 0.4375 至此，我们得到了基于稳定性优化的参数b和（的设计方法： (1)根据工艺选取及电路设计的实际情况，估算出式(2-13)中的环路参数的相对变 化量（△Kvco/Kvco,△Iep/Iep,△R/R1,△C/Ci,△NN),并计算出工艺变化因子amin-P Amax-P (2)根据式(2-l4)所示的Amin和cmax的定义式计算设计变化因子amim和amax。 (3)一般情况下取b=10,即对应着amim=0.6109;amax=1.637。如果(amim-P,amax-p)的 范围小于(0.6109,1.637)，无需进行任何补偿，直接可以用(b,℃)=(10,1.0388)去计 算其他环路参数；如果(amm-P,amax-p)的范围大于(0.6109,1.637)，需要采用加倍- 减半电荷泵电流的方法使amim=0.305;amax=3.274。此时如果(amim-P,max-p)的范围 小于(0.305,3.274)，则可以用(b,)=(10,1.0388)去计算其他环路参数：反之需要改 变电容比b重新计算。 2.3.2基于稳定性优化的四阶环路的分析 E(z) 回Q包f0回回1 Heve 1.5 图2.l3三阶、三比特sigma-delta调制器 图2.13所示的三阶、三比特量化的sigma-delta调制器结构具有很好的带内 噪声整形特性。其中的×2、×1.5、×0.5电路都可以通过移位器(shifter)简单实现。 因此本调制器可以有很简单的数字结构。推导可得它在相位域的单边带功率谱密 12

复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 围。其中最有效的方法就是加倍或减半电荷泵的电流以使(2-14)中αmin和αmax的分 母减小或增加。表 2-3 给出了b、ζopt、αmin和αmax几个量之间的数值关系。可以看 到，随着电容比b的增加，最优的阻尼因子ζopt也在增加，并且变化裕量也在增加， 也就是说环路更加稳定。 表 2-3 电容比与最优阻尼因子、最优变化因子、边界变化因子关系表 电容比 b 9 10 12 20 αopt 1.0119 1.0311 1.0766 1.2702 ζopt 1.0201 1.0388 1.073 1.1814 αmax 1.5548 1.637 1.7878 2.2855 αmin 0.6431 0.6109 0.5594 0.4375 至此，我们得到了基于稳定性优化的参数 b 和 ζ 的设计方法： (1)根据工艺选取及电路设计的实际情况，估算出式(2-13)中的环路参数的相对变 化量(ΔKvco/Kvco, ΔIcp/Icp, ΔR1/R1, ΔC1/C1, ΔN/N)，并计算出工艺变化因子αmin－P、 αmax－P。 (2)根据式(2-14)所示的αmin和αmax的定义式计算设计变化因子αmin和αmax。 (3)一般情况下取b=10，即对应着αmin=0.6109；αmax=1.637。如果(αmin－P,αmax－P)的 范围小于(0.6109,1.637)，无需进行任何补偿，直接可以用(b, ζ)= (10, 1.0388)去计 算其他环路参数；如果(αmin－P,αmax－P)的范围大于(0.6109,1.637)，需要采用加倍- 减半电荷泵电流的方法使αmin=0.305；αmax=3.274。此时如果(αmin－P,αmax－P)的范围 小于(0.305,3.274)，则可以用(b, ζ)= (10, 1.0388)去计算其他环路参数；反之需要改 变电容比b重新计算。 2.3.2 基于稳定性优化的四阶环路的分析 图 2.13 三阶、三比特 sigma-delta 调制器 图 2.13 所示的三阶、三比特量化的sigma-delta调制器结构[13]具有很好的带内 噪声整形特性。其中的×2、×1.5、×0.5 电路都可以通过移位器(shifter)简单实现。 因此本调制器可以有很简单的数字结构。推导可得它在相位域的单边带功率谱密 12

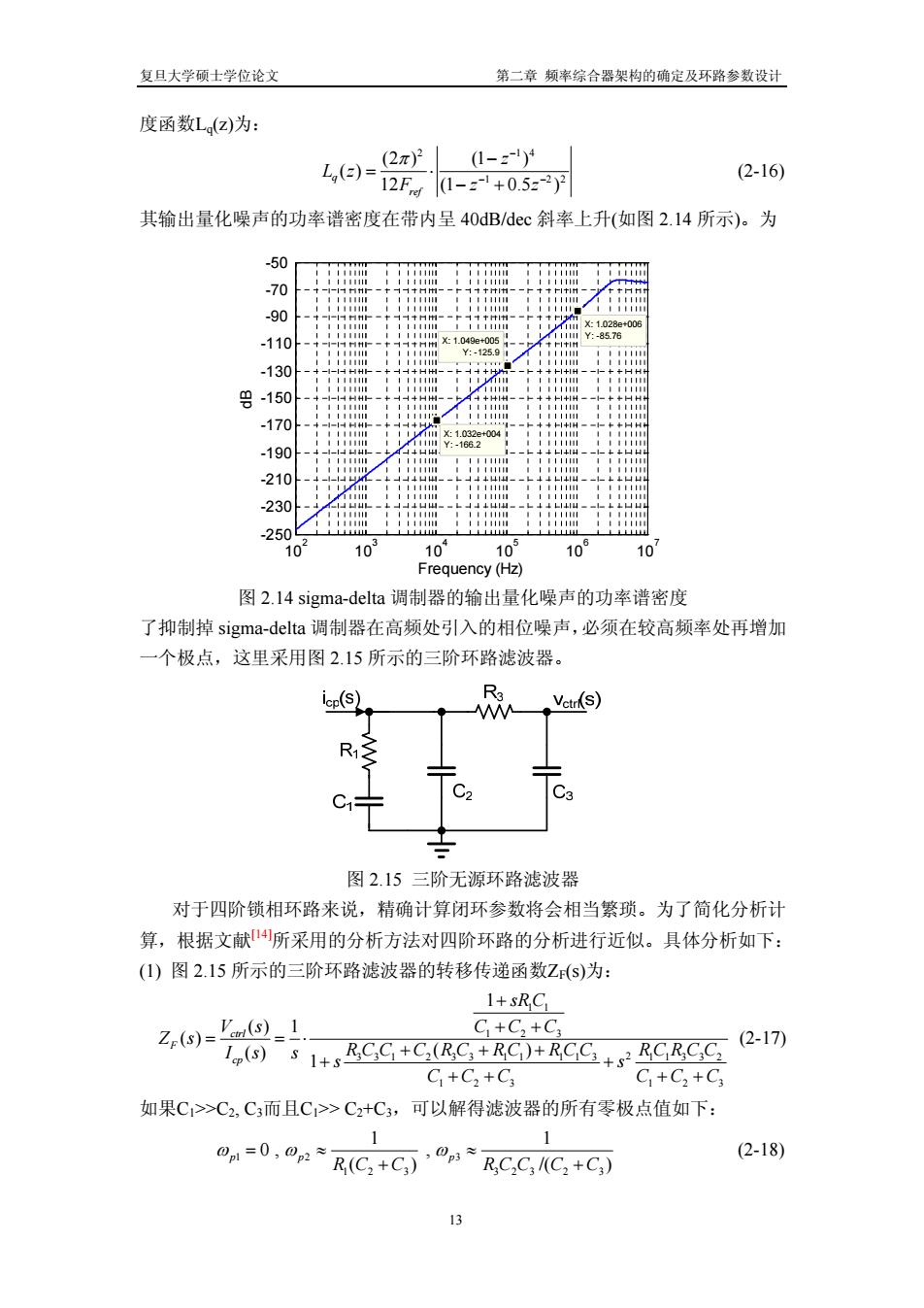
复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 度函数L(z)为： L,()= (2π)2 (1-z-)4 2Fd (2-16) (1-z1+0.5z-2)2 其输出量化噪声的功率谱密度在带内呈40dB/dec斜率上升（如图2.14所示）。为 -50 -70 tm- +十 -90 -r 1111114 X:1.028e+006 x1.049e+0051-- Y:-85.76 -110 Y:-125.9 -130 H44HHI-- -150 -170 ■ X:1.032e+004 H :-166.2 -190 11111 -210 11111 230 111 250 10 10 10 10 10 10 Frequency(Hz) 图2.14 sigma-delta调制器的输出量化噪声的功率谱密度 了抑制掉sigma-delta调制器在高频处引入的相位噪声，必须在较高频率处再增加 一个极点，这里采用图2.15所示的三阶环路滤波器。 R Vetr[S) R 图2.15三阶无源环路滤波器 对于四阶锁相环路来说，精确计算闭环参数将会相当繁琐。为了简化分析计 算，根据文献所采用的分析方法对四阶环路的分析进行近似。具体分析如下： (1)图2.15所示的三阶环路滤波器的转移传递函数Z(s)为： 1+SRC Z(s)= '(s-1 C+C2+C3 (2-17) I()1+RCC+C,(RC3+RC)+RCCRCRCC, C,+C2+C3 C+C2+C3 如果C1>>C2,C3而且C>C2+C3,可以解得滤波器的所有零极点值如下： 1 1 0p1=0,0p2 R(C+C3),D≈ (2-18) RC2C31(C2+C3) 13

复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 度函数Lq(z)为： 2 1 1 2 (2 ) (1 ) ( ) 12 (1 0.5 ) q ref z L z F zz π − − − − = ⋅ − + 4 2 (2-16) 其输出量化噪声的功率谱密度在带内呈 40dB/dec 斜率上升(如图 2.14 所示)。为 102 103 104 105 106 107 -250 -230 -210 -190 -170 -150 -130 -110 -90 -70 -50 X: 1.032e+004 Y: -166.2 X: 1.049e+005 Y: -125.9 X: 1.028e+006 Y: -85.76 Frequency (Hz) dB 图 2.14 sigma-delta 调制器的输出量化噪声的功率谱密度 了抑制掉 sigma-delta 调制器在高频处引入的相位噪声，必须在较高频率处再增加 一个极点，这里采用图 2.15 所示的三阶环路滤波器。 图 2.15 三阶无源环路滤波器 对于四阶锁相环路来说，精确计算闭环参数将会相当繁琐。为了简化分析计 算，根据文献[14]所采用的分析方法对四阶环路的分析进行近似。具体分析如下： (1) 图 2.15 所示的三阶环路滤波器的转移传递函数ZF(s)为： 1 1 123 331 2 33 11 113 113 3 2 2 123 1 2 1 ( ) 1 ( ) ( ) ( ) 1 ctrl F cp sR C V s CCC Z s 3 Is s R CC C RC RC RCC RCRCC s s CCC CCC + + + = =⋅ + ++ + + + + + + (2-17) 如果C1>>C2, C3而且C1>> C2+C3，可以解得滤波器的所有零极点值如下： 1 2 3 1 2 3 323 2 3 1 1 0 , , ( ) /( p p p R C C RCC C C ) ωω ω =≈ ≈ + + (2-18) 13

复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 1 0= (2-19) RC 因此环路滤波器的近似表答式为： 1 Z(s)= 1+s/@ (2-20) s(C1+C2+C3)(1+s/o2)1+s/op3） (2)确定环路滤波器的电阻电容值 由式(2-18)可知电容C3会改变环路的极点op2。为了满足op2=10oz,需满足： G+C=9 (2-21) 10 为了滤除sigma-delta调制器在1MHz处的噪声能量，同时不影响四阶环路的相位 裕度，第三个高频极点o3的位置大致处于12o左右。根据(2-18)式可得 1 C2+C3 pR.C:C,/(C:+C3)RC;C, (2-22) 为了降低电阻R3的噪声贡献，需要使R3的值最小，由式(2-18)可得： C2+C32 .2 R3= (2-23) @pC:C3 @pC3 当C2=C,时，R3值最小。可以求出三个电容之间的关系为： 6-G号 (2-24) 电阻R3的大小为： R3= (2-25) QpC3 (3)近似产生的偏差 四阶系统的开环传递函数为： Ho(s)=- cpKvco.Z(s) (2-26) 2πN·s 它所对应的闭环传递函数Hc(s)的表达式为： H(S)= NH (s) (2-27) 1+H(s) 近似后的四阶系统开环传递函数的表达式如下： H(S)= IcpKvco 1+s0 (2-28) 2πN(C+C2+C3)s2(1+s/o2)1+s/0p3) 它所对应的闭环传递函数H(S)的表达式为： H(s)= NH(s) (2-29) 1+H.(s) 为了验证近似分析的合理性，需要对比式(2-26)和(2-28)所对应的波特图以及阶跃 14

复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 1 1 1 ωz = RC (2-19) 因此环路滤波器的近似表答式为： 123 2 3 1 1 ( ) ( ) (1 )(1 z f p p s Z s sC C C s s ) ω ω ω + = ⋅ ++ + + (2-20) (2) 确定环路滤波器的电阻电容值 由式(2-18)可知电容C3会改变环路的极点ωp2。为了满足ωp2=10ωz，需满足： 1 2 3 10 + = C C C (2-21) 为了滤除sigma-delta调制器在 1MHz处的噪声能量，同时不影响四阶环路的相位 裕度，第三个高频极点ωp3的位置大致处于 12ωc左右。根据(2-18)式可得 2 3 323 2 3 323 1 /( ) ω + 3 ≈ = + p C C R CC C C RCC (2-22) 为了降低电阻R3的噪声贡献，需要使R3的值最小，由式(2-18)可得： 2 3 3 323 33 2 ω ω + = ≥ p p C C R CC C (2-23) 当C2=C3时，R3值最小。可以求出三个电容之间的关系为： 1 2 3 20 = = C C C (2-24) 电阻R3的大小为： 3 3 3 2 p R ω C = (2-25) (3) 近似产生的偏差 四阶系统的开环传递函数为： ( ) ( ) 2 CP VCO O I K Hs Zs π N s = ⋅ ⋅ F (2-26) 它所对应的闭环传递函数HC(s)的表达式为： ( ) ( ) 1 ( o C o NH s H s H s = + ) (2-27) 近似后的四阶系统开环传递函数的表达式如下： 2 123 2 3 1 ( ) 2 ( ) (1 )(1 CP VCO z o p p I K s H s NC C C s s s ) ω π ω ω + = ⋅ ++ + + (2-28) 它所对应的闭环传递函数Hc(s)的表达式为： ( ) ( ) 1 ( o c o NH s H s H s = + ) (2-29) 为了验证近似分析的合理性，需要对比式(2-26)和(2-28)所对应的波特图以及阶跃 14

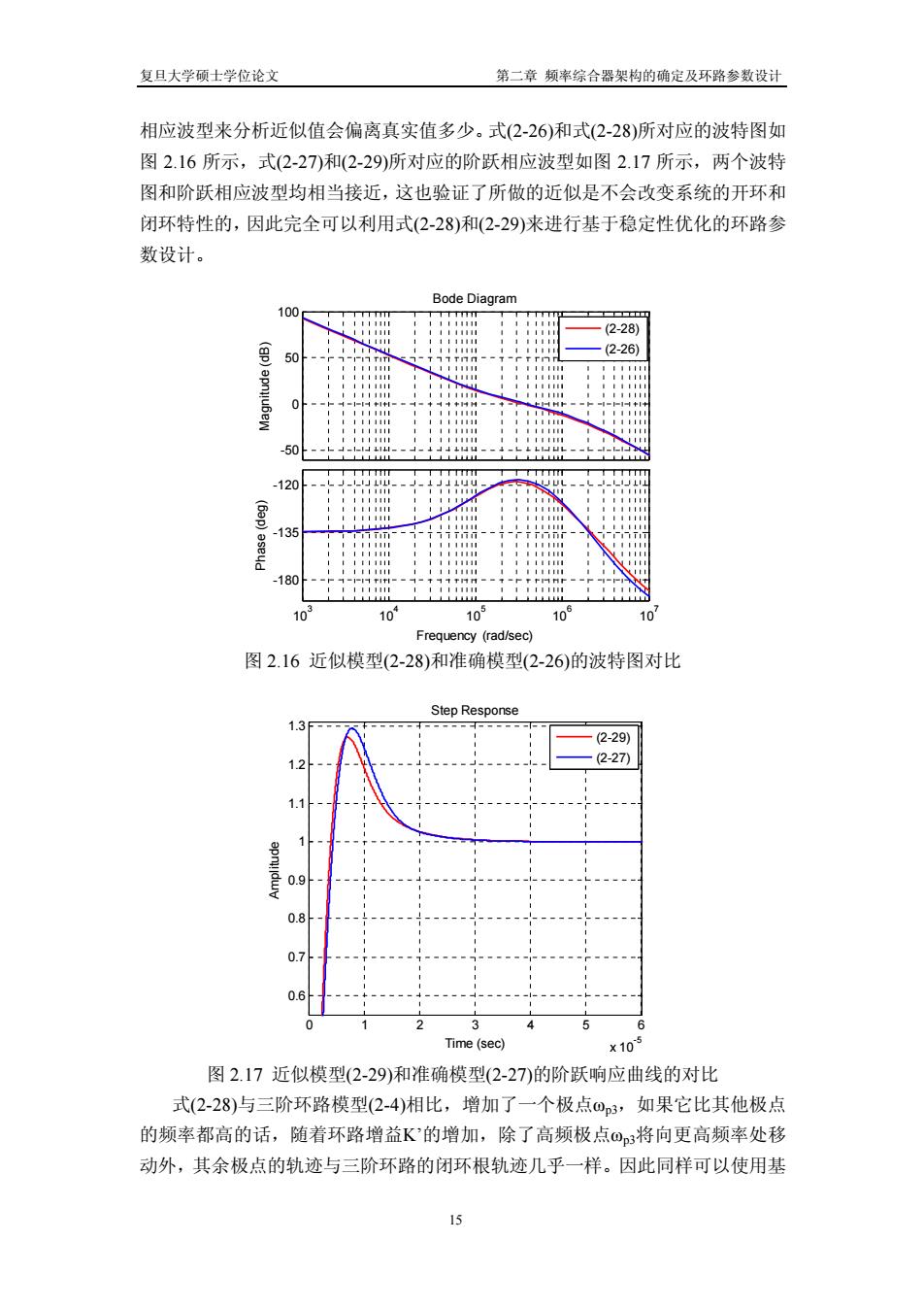
复旦大学硕士学位论文 第二章频率综合器架构的确定及环路参数设计 相应波型来分析近似值会偏离真实值多少。式(2-26)和式(2-28)所对应的波特图如 图2.16所示，式(2-27)和(2-29)所对应的阶跃相应波型如图2.17所示，两个波特 图和阶跃相应波型均相当接近，这也验证了所做的近似是不会改变系统的开环和 闭环特性的，因此完全可以利用式(2-28)和(2-29)来进行基于稳定性优化的环路参 数设计。 Bode Diagram 100 (2-28) (2-26) 50 HH 111111 50 120 (6ap) 411110 135 -出 111 II 180 11111 10 10 10 10 10 Frequency (rad/sec) 图2.16近似模型(2-28)和准确模型(2-26)的波特图对比 Step Response (2-29) (2-27) 1.1 0.9 0. 0.6 0 Time(sec) ×10 图2.17近似模型(2-29)和准确模型(2-27)的阶跃响应曲线的对比 式(2-28)与三阶环路模型(2-4)相比，增加了一个极点03，如果它比其他极点 的频率都高的话，随着环路增益K'的增加，除了高频极点O3将向更高频率处移 动外，其余极点的轨迹与三阶环路的闭环根轨迹几乎一样。因此同样可以使用基 15

复旦大学硕士学位论文 第二章 频率综合器架构的确定及环路参数设计 相应波型来分析近似值会偏离真实值多少。式(2-26)和式(2-28)所对应的波特图如 图 2.16 所示，式(2-27)和(2-29)所对应的阶跃相应波型如图 2.17 所示，两个波特 图和阶跃相应波型均相当接近，这也验证了所做的近似是不会改变系统的开环和 闭环特性的，因此完全可以利用式(2-28)和(2-29)来进行基于稳定性优化的环路参 数设计。 -50 0 50 100 Magnitude (dB) 103 104 105 106 107 -180 -135 -120 Phase (deg) Bode Diagram Frequency (rad/sec) (2-28) (2-26) 图 2.16 近似模型(2-28)和准确模型(2-26)的波特图对比 0 1 2 3 4 5 6 x 10-5 0.6 0.7 0.8 0.9 1 1.1 1.2 1.3 Step Response Time (sec) Amplitude (2-29) (2-27) 图 2.17 近似模型(2-29)和准确模型(2-27)的阶跃响应曲线的对比 式(2-28)与三阶环路模型(2-4)相比，增加了一个极点ωp3，如果它比其他极点 的频率都高的话，随着环路增益K’的增加，除了高频极点ωp3将向更高频率处移 动外，其余极点的轨迹与三阶环路的闭环根轨迹几乎一样。因此同样可以使用基 15