《数字信号处理》课程教学资源（教案讲义）ch5 FIR数字滤波器的设计

P-12元元0线性相位FIR滤波器频率响应一般形式可写为H(eig)=ei-0.5M+β) A(2)表5-1四种线性相位FIR滤波器的性质1IIIIIV类型偶奇偶奇阶数M[]的对称性偶对称偶对称奇对称奇对称A()关于O-0的对称性奇对称偶对称偶对称奇对称A(2)关于0=元的对称性偶对称奇对称奇对称偶对称2元4元2元4元A(2)的周期β000.5元0.5元00A(0)任意任意A(m)00任意任意LP,HP,B LP, BP可适用的滤波器类型微分器,Hilbert微分器,HilbertP,BS等变换器，HP变换器线性相位系统H(z)的零点分布特性h[k]=±h[M -k] = H()=±z-MH(--')Z=0不可能有系统的零点.zk是系统的零点，则zk-I也是系统的零点。·:h[K]是实的,re-ioZh=ejorileror'e-in

线性相位 FIR 滤波器频率响应一般形式可写为 (e ) e ( ) j j( 0.5 ) =    H A - M  表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A 任意 0 0 任意 可适用的滤波器类型 LP,HP,B P,BS等 LP, BP 微分器,Hilbert 变换器 微分器,Hilbert 变换器，HP 表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 表 5-1 四种线性相位 FIR 滤波器的性质 类型 I II III IV 阶数 M 偶 奇 偶 奇 h[k]的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 偶对称 奇对称 奇对称 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A()关于=的对称性 偶对称 奇对称 奇对称 偶对称 A()的周期 2 4 2 4  0 0 0.5 0.5 A 任意 任意 0 0 A 任意 0 0 任意 可适用的滤波器类型 LP,HP,B P,BS等 LP, BP 微分器,Hilbert 变换器 微分器,Hilbert 变换器，HP 线性相位系统 H(z)的零点分布特性 h[k] = h[M − k] ( ) ( ) − −1  H z = z H z M • z=0 不可能有系统的零点 • zk 是系统的零点，则 zk-1 也是系统的零点。 • h[k]是实的, , k j k k z r e  = , k j k r e −  , 1 k j k r e − −  k j k r e −1  0 A ( ) 1  

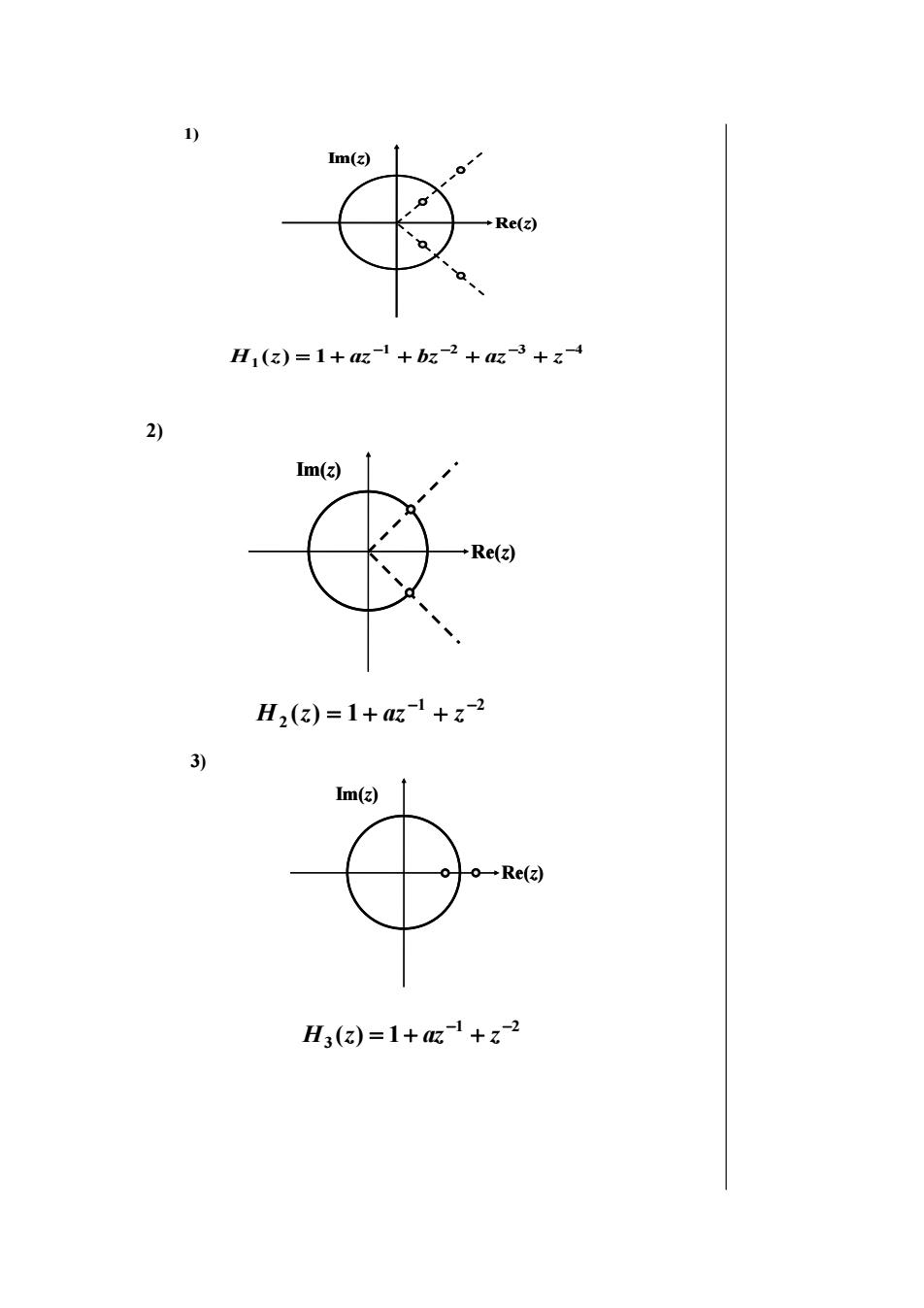
1)Im(z)Re(z)Hi(z) =1+ az-1 + bz-2 + az-3 + z-42)Im(z)+Re(z)H2(z) =1+ az-1 + z-23)Im(z)o-Re(z)?H3(z) =1+az- + z-2

1) 1 2 3 4 1 ( ) 1 − − − − H z =  az  bz  az  z Re(z) Im(z) Re(z) Im(z) 2) Re(z) Im(z) Re(z) Im(z) 1 2 2 ( ) 1 − − H z =  az  z Re(z) Im(z) Re(z) Im(z) 1 2 3 ( ) 1 − − H z =  az  z 3)

4)Im(z)+Re(z)H4(z) =1± z-1任意线性相位系统是上述四种子系统的组合·h[K]奇对称时，H(z)在z=1处一定有奇数阶零点。四种不同类型的线性相位系统在zk=±1的零点：(1)I型FIR滤波器(M为偶)：在zk-1和zk=-1无零点或者有偶数个零点。(2)II型FIR滤波器(M为奇）：在zk=-1有奇数个零点，在zk-1无零点或者有偶数个零点。(3)III型FIR滤波器(M为偶)：在zk=1和zk=-1有奇数个零点。(4)IV型FIR滤波器(M为奇)：在zk=1有奇数个零点，在zk--1无零点或者有偶数个零点

Re(z) Im(z) Re(z) Im(z) 4) 1 4 ( ) 1 − H z =  z •任意线性相位系统是上述四种子系统的组合 •h[k]奇对称时，H(z)在z=1处一定有奇数阶零点。 四种不同类型的线性相位系统在 zk=1 的零点： (1)I 型 FIR 滤波器(M 为偶)： 在 zk=1 和 zk= -1 无零点或者有偶数个零点。 (2)II 型 FIR 滤波器(M 为奇)： 在 zk= -1 有奇数个零点，在 zk=1 无零点或者有偶数个零点。 (3)III 型 FIR 滤波器(M 为偶)： 在 zk=1 和 zk= -1 有奇数个零点。 (4)IV 型 FIR 滤波器(M 为奇)： 在 zk=1 有奇数个零点，在 zk=-1 无零点或者有偶数个零点

5.2窗函数法设计FIR滤波器·最小积分平方误差设计FIR滤波器·吉伯斯(Gibbs)现象·常用窗函数窗函数法的MATLAB实现5.2.1最小积分平方误差设计FIR滤波器问题：已知Hd(ejW)，设计使其频率响应逼近Hd(ejW)。Th[k]-kH(-)=k=01T Ha(e)eind2h,[k]=-2元ha[K]一般情况下是无穷序列，需对其进行截断。方案1：设Ha(ei)是实偶函数，则ha[K]是实偶对称的。设 M=-2K, w[K]=RN+I[K]h [K]- ha [k-K]RN+1[K]h [M-k]= hd [M-k-M/2] RN+1 [K]= hd [-(k-N /2] RN+1 [K] = hd [k-M]RN+1[K] = h[K]例：设计一个线性相位的FIR滤波器。其频率响应能逼近截频为Wc的理想低通。[12≤2。解：设H(ej)=lo其他12eSa(2,k)f1.e/ dQ - -h,[k]-2元20元h[k]= h,[k- M /2]- α=sa(2,(k- M /2),0 ≤k≤ M2元方案2：设Ha(ej2)为Ha (ei?)=Ad(2)exp(i( -0.5MQ +b)I型和II:b=0III型和IV:b=元/2。h [K]= ha [K]RN+1[K]例：设计一个线性相位的FIR滤波器。其频率响应能逼近截频为Wc的理想低通。解：设j0.5M220≤H.(e其他0Sa(Q,(k - M /2)j0.5m.ejkndQ=h,[k] 2元元0

5.2 窗函数法设计 FIR 滤波器 • 最小积分平方误差设计 FIR 滤波器 • 吉伯斯(Gibbs)现象 • 常用窗函数 • 窗函数法的 MATLAB 实现 5.2.1 最小积分平方误差设计 FIR 滤波器 问题：已知 Hd(ejW)，设计 使其频率响应逼近 Hd(ejW)。 k M k H z h k z − = ( ) =  [ ] 0 =    −  ( ) d 2 1 [ ] j jk d d h k H e e    hd [k]一般情况下是无穷序列，需对其进行截断。 方案 1：设 Hd (ej  )是实偶函数， 则 hd [k]是实偶对称的。 设 M=2K, w[k]=RN+1[k] h [k]= hd [k-K]RN+1[k] h [M-k]= hd [M-k-M/2] RN+1 [k] = hd [-(k-N /2)] RN+1 [k] = hd [k-M]RN+1[k] = h[k] 例：设计一个线性相位的 FIR 滤波器。其频率响应能逼近截频 为 Wc 的理想低通。 解：设       =  0 其他 1 ( ) d j c H e 1 Sa( ) 2 1 h [k] e d kc jk c d c c   =   =   −    h k hd k M c c k − M   k  M  [ ] = [ − / 2] = Sa ( / 2 ,0  方案 2：设 Hd (ej  )为 Hd (ej  )=Ad(  )exp(j( -0.5M  +b)) I 型和 II: b=0 ; III 型和 IV:b= /2。 h [k]= hd [k]RN+1[k] 例：设计一个线性相位的 FIR 滤波器。其频率响应能逼近截频 为 Wc 的理想低通。 解：设        = −   0 其他 e 0 ( ) j0.5 d c M j H e e Sa ( / 2) 2 1 [ ] j0.5 h k e d c c k M M j k d c c  −  =   = −    −   

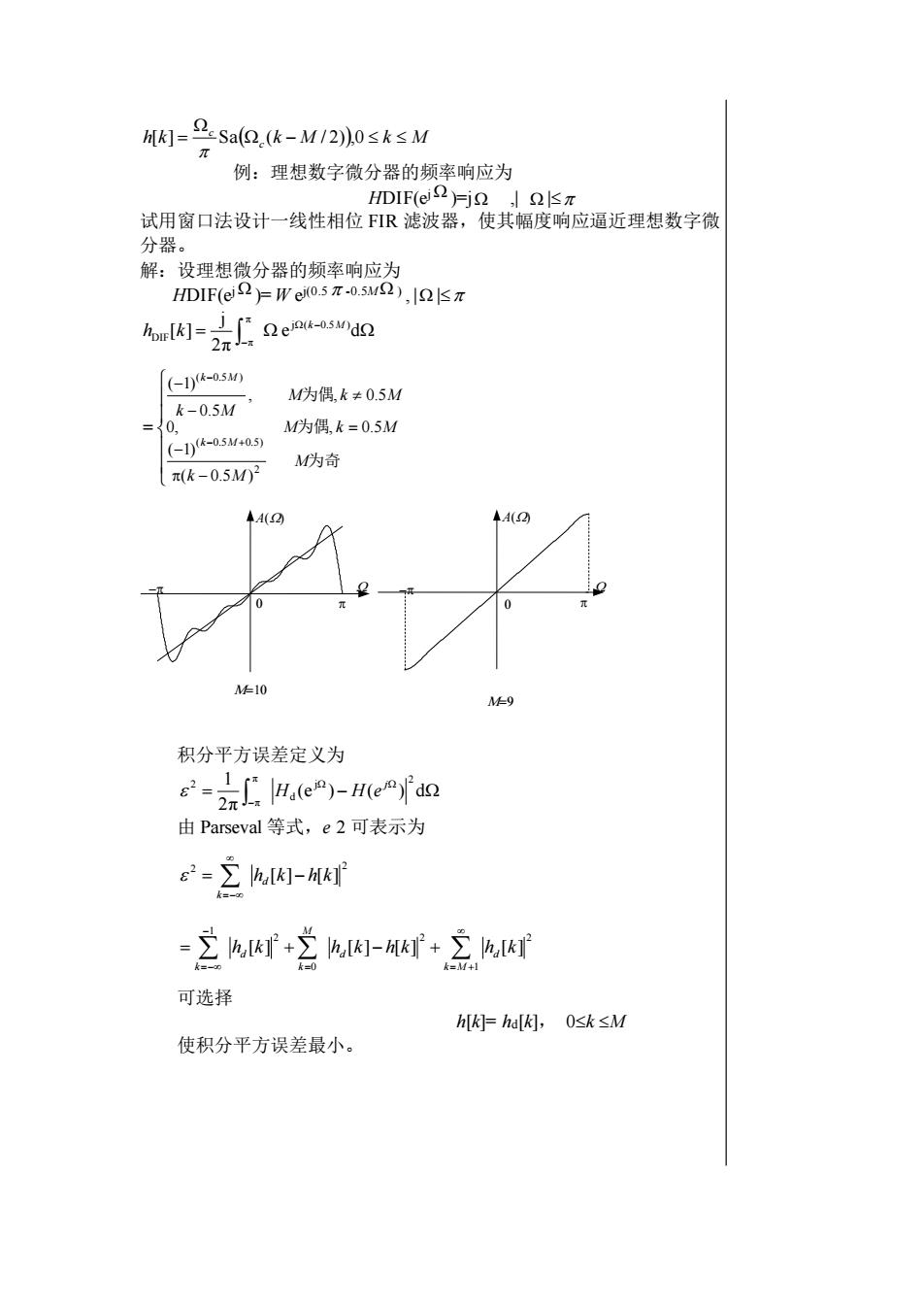
h[k)- 2cSa(2,(k-M /2),0≤k≤MT例：理想数字微分器的频率响应为HDIF(ej)j 试用窗口法设计一线性相位FIR滤波器，使其幅度响应逼近理想数字微分器。解：设理想微分器的频率响应为HDIF(e)We(0.5元-0.5M),[" Qejin(k-0.5M)dQhpr[k]=-2元／(-1)(k-0.5M)M为偶，k*0.5Mk-0.5MM为偶,k=0.5M=20(1)(k0.5M+0.5)M为奇元(k-0.5M)24A(2)A(2)LM-10M-9积分平方误差定义为- Md(en)-He)da由Parseval等式，e2可表示为”- 2 h[K]- [K]Z h,[Kk]+≥ h,[k]- [k]+Z (h,[k]"k=M+I可选择h[k]= ha[K],0<k≤M使积分平方误差最小

h k c c k − M   k  M  [ ] = Sa ( / 2) ,0  例：理想数字微分器的频率响应为 HDIF(e j  )=j  ,|  |  试用窗口法设计一线性相位 FIR 滤波器，使其幅度响应逼近理想数字微 分器。 解：设理想微分器的频率响应为 HDIF(ej  )= W e j(0.5  -0.5M  ) , |  |  =    − − e d 2π j [ ] j ( 0.5 ) π π DIF k M h k        =  − − =  − − −  − 为奇 为偶 为偶 M k M M k M M k M k M k M k M ( 0.5 ) ( 1) 0, , 0.5 , , 0.5 0.5 ( 1) 2 ( 0.5 0.5) ( 0.5 ) A()  −    − A()   = = 积分平方误差定义为 = −    − (e ) ( ) d 2π 1 2 j d π π 2 j  H H e 由 Parseval 等式，e 2 可表示为 2 2 h [k] h[k] d k =  −  =−  2 1 2 0 2 1 h [k] h [k] h[k] h [k] d k M d M k d k     = =  − =− =  −  可选择 h[k]= hd[k]， 0k M 使积分平方误差最小