
U U uc=P.-P (Pev-Pe:) =0+=0, 行0=0 t>0 >0 2im t=tn时i最大 LCP2 RCP+1=0 4z(0)=U0 duc.-CUpe) i=-C dt 0<t<tm (P2-P) i增加,u>0 -U0 (:) t>im L(P:-P) i减小,u虹<0 di ul L -U(P.en-Pjet) t=2tm时W红极小 dt (P,-P) t>2tmuu衰减加快
( ) ( ) ( ) ( ) 1 2 1 2 2 1 0 1 2 1 2 2 10 p t p t C p t p t e e L P P U p p e p p e P P CU dt du i C − − − = − − − = − = t=0+ i=0 , t= i=0 t = tm 时i 最大 0< t < tm i 增加, u L>0 t > tm i 减小, u L <0 ( ) t = 2 tm 时 u L 极小 ( ) 1 2 1 2 2 1 0 p t p t L P e P e P P U dt di u L − − − = = 2 tm u L tm i u L (0)= U0 t > 2 tm u L 衰减加快 1 0 2 LCP + RCP + = t> 0 i>0 t U0 u c ( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − =
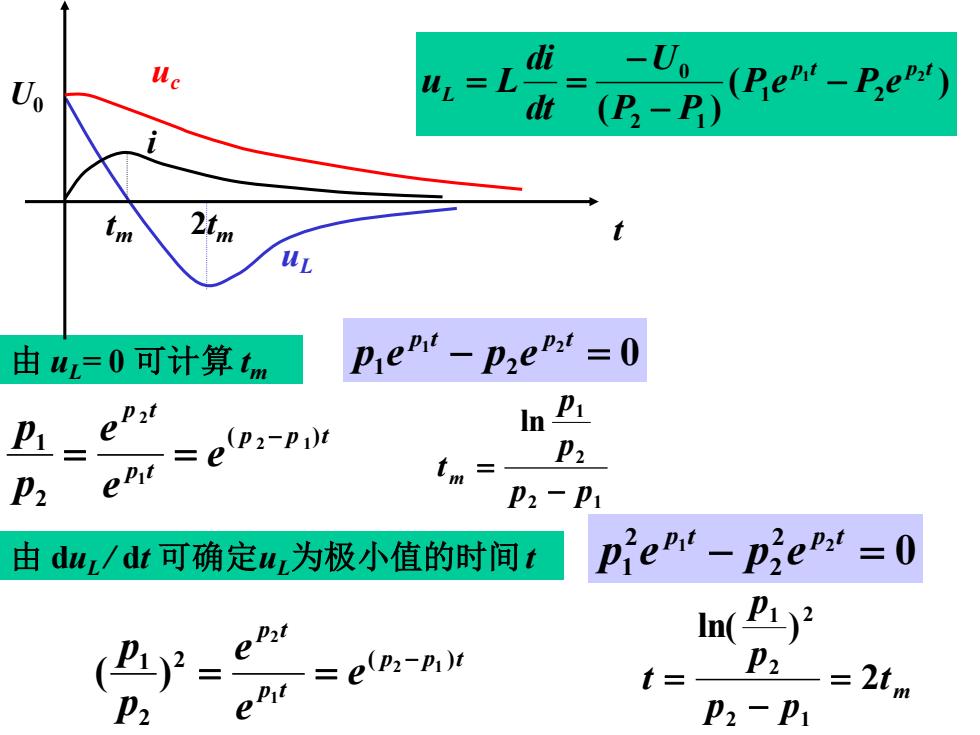
uc di U uL=L -U(Ben-P.e:) dt (P,-P) 由u=0可计算tm prepu-pzea=0 = =e(pz-p m P2 P2 tm= P2-P1 由duu/dt可确定w,为极小值的时间t piepu-pieps= ()=e In( =e(p2-p)t f= p2一=2tm P2 P2-P1
由 uL= 0 可计算 tm 0 1 2 1 − 2 = p t p t p e p e p p t p t p t e e e p p 2 ( ) 2 1 2 1 1 2 ( ) − = = 2 1 2 1 ln p p p p t m − = 由 duL / dt 可确定uL为极小值的时间t 0 1 2 2 2 2 1 − = p t p t p e p e p p t p t p t e e e p p ( ) 2 1 2 1 1 2 − = = m t p p p p t 2 ln( ) 2 1 2 2 1 = − = 2tm uL tm i t U0 uc ( ) ( ) 1 2 1 2 2 1 0 p t p t L P e P e P P U dt di u L − − − = =
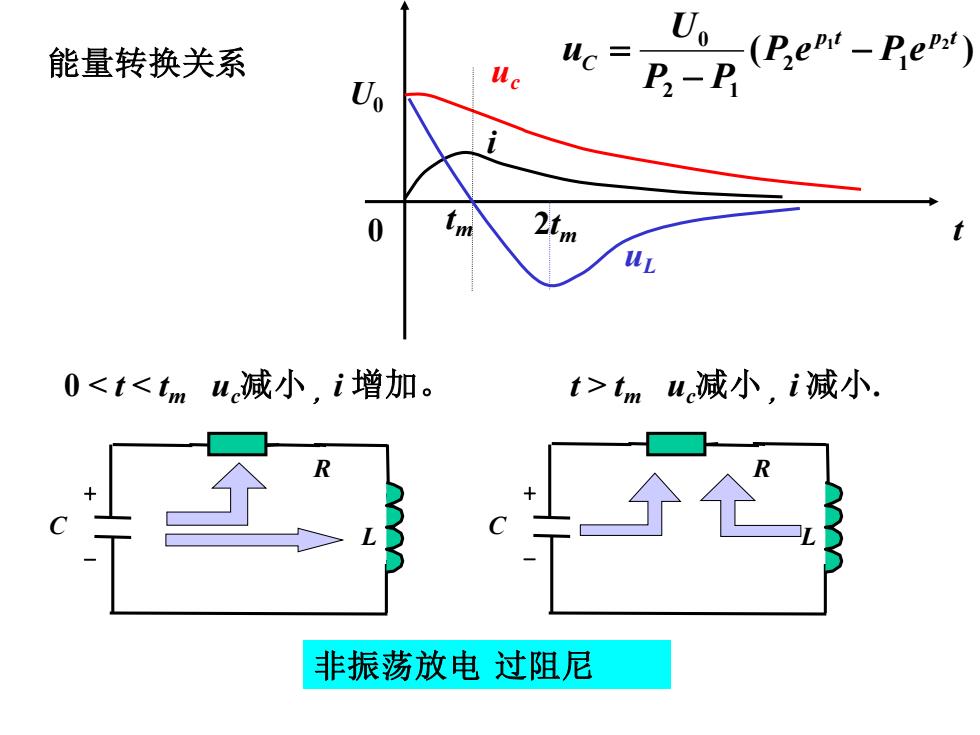
能量转换关系 ,(Pem-Pe:) Uo uc=P.-P 2im 0<t<tmuc减小,i增加。 t>tmu减小,i减小. 非振荡放电过阻尼
能量转换关系 0 < t < tm uc减小, i 增加。 t > tm uc减小, i 减小. R L C + - R L C + - t U0 uc tm i 0 非振荡放电 过阻尼 ( ) 1 2 2 1 2 1 0 p t p t C P e P e P P U u − − = 2tm uL
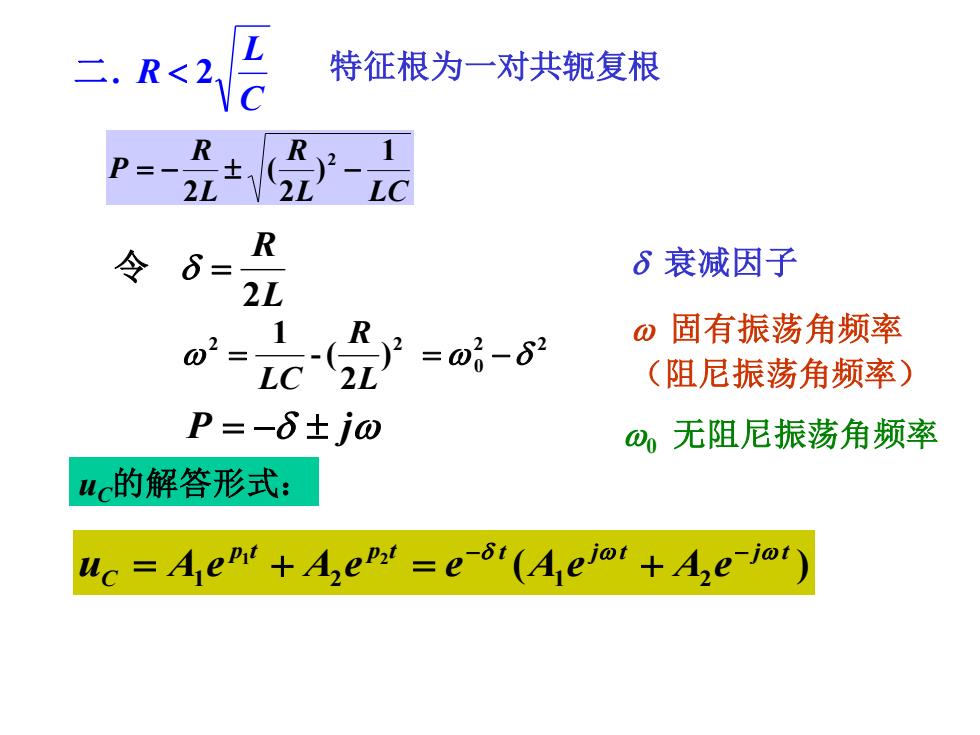
R 特征根为一对共轭复根 R 2LV 2L' 令 R 6衰减因子 21 02 1 R =06-62 ω固有振荡角频率 (阻尼振荡角频率) P=-6±jω ①,无阻尼振荡角频率 uc的解答形式: uc Aen+Aer:=e(A ejoi+Ae-io)
. 2 C L 二 R 特征根为一对共轭复根 L LC R L R P 1 ) 2 ( 2 2 = − − P = − j 2L R 令 = uC的解答形式: ( ) 1 2 1 2 1 2 p t p t t j t j t C u A e A e e A e A e − − = + = + 2 2 0 2 2 ) 2 -( 1 = = − L R LC 衰减因子 固有振荡角频率 (阻尼振荡角频率) 0 无阻尼振荡角频率
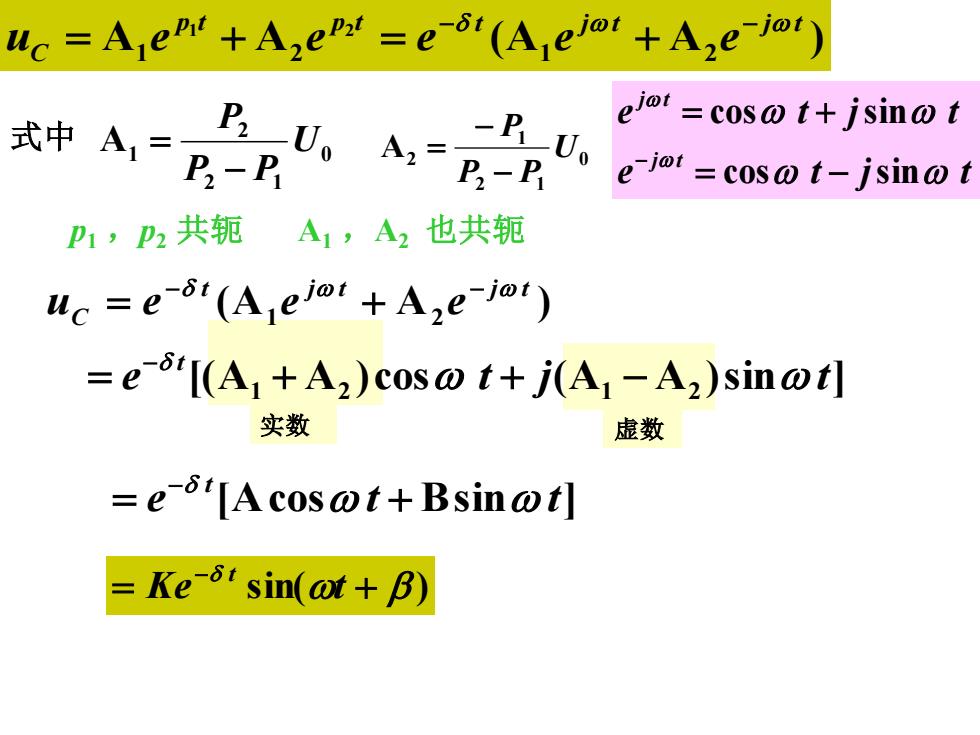
uc =A ep+Azeps =e-(A eiot+A,e-io) 式中A=D,-B ejot=cos@t+jsin@t P-P e-iot =cos@t-jsin@t P1,P2共轭A1,A2也共轭 uc =e(Ajeio+Aze-i) =e'[(A+A2)cos@t+j(A1-A2)sin@t] 实数 虚数 =e[Acos@t+Bsin@t] Ke-5'sin(at+B)
实数 虚数 e t j t e t j t j t j t cos sin cos sin = − = + − [(A A )cos (A A )sin ] 1 2 1 2 e t j t t = + + − − p1 ,p2 共轭 A1 ,A2 也共轭 A A (A A ) 1 2 1 2 1 2 p t p t t j t j t C u e e e e e − − = + = + sin( ) = + − Ke t t (A A ) 1 2 t j t j t C u e e e − − = + e [Acos t Bsin t] t = + − 0 2 1 2 A1 U P P P − = 0 2 1 1 A2 U P P P − − 式中 =