
的距离趋干无限小时的一种极限。因此,如定义电偶极矩P为(9) 电偶极子的电位,式(8)变为PcOse(10)uI对位下任意点「",沿着一普通轴放置的电偶极了,式(10)的另一种更一般的写法是引进偶极矩矢量。定义这个矢量具有量值P,方向是沿着两电荷的轴线从负电荷指向正电荷。当把单位失量-定义为从点r"(电偶极子所在处)指向观察点r,由式(10)可得到广义的电位公式0-(11)无限远处的一对等量异号电荷ilr以下考虑对位于图4.4.2a原点附近的两电A荷之间的观察者看来的电场形状。现在我们限于关心与原点的距离比起电荷间距&要小得多的情况。实际上,两个电荷各自在十和一方向的无穷远处。借助于图4.4.4和三维毕达哥拉斯定理,从电荷所在点到观察点的距离可用球标表示为图1.4.4电荷趋于无限远处的相对位移=(号rcoso)+(rsino),r-=/(号+rcoso) +(rsino)(12)在这些表达式中,&比起来要大,因此它们又可应用式(7)展开,且仅保留的线性项+co0cs(13)把这些近似式代人式(2),可得与位于轴无穷远处的电荷相关的所求电位的表达式@—2(g/a2rcosg(14)注意到≥=Tcos,所以看起来复杂的电场在球坐标系中简单地为2g/2z@-(15)坐标也可以看成是笛卡儿坐标中的,并且电场可通过用笛卡儿坐标的梯度算子求出。因此,图4.4.2c中所示的等位面是水平面。由此可知电场强度是均勾的并且方向朝下。注意到由式(15)所得电场也就是当点电荷位干所关心点的上方和下方号距离时通过直接计算式(1.3.12)所得的电场值。其他的电荷奇异性二维的偶极子由一对带相反电荷的平行线组成,而不是一对点电荷。在垂直于平行线的平面78

中,应用极坐标系,等位线看起来类似于图4.4.26中的等位线。但是,在三维坐标中等位面是圆形截面的柱体,而完全不象三维电偶极子的等位面是旋转成的封闭面。二维电偶极子的电场将要在习题4.4.1和4.4.2中推导,并将给出电位以供参考有无数种电荷奇异性。“高阶”的电荷奇异性之一是在习题4.4.3和4.4.4中说明的四极子电场。在第5 章中我们还将见到这些相同的电位4.5对特定电荷分布的泊松方程的解答现在,用叠加原理来求解任何给定电荷分布p(r)的泊松方程。前一节对于奇异的电荷分布所出的论证提供了解决问题的方法。为了把任意的电荷密度分布表示成许多单元的电荷分布的总和这一目的,我们把也/xy.z)荷密度所占据的空间细分成许多大小为 dz(x.y,z)dy'dz”的单元体积。每个单元由笛卡儿坐标(a,9,z)表示,如图4.5.1所示。位丁坐标(t"",z')处的-个单元体积所带电荷为dq= p(r"da'dy'dz'- p(r')do*(1)图4.5.1位于点上的单元体积电荐在观察点,上产生的电位现在,我们把由电荷密度p引起的总电位表示成由位于点的微分电荷元产生的,由式(1)表示的电位d@的叠加。注意到这些单元电荷分布中的每一个在位于r’点处的体积元du"以外,各点上电荷密度都为零。所以,它们代表「量值由式(1)给定的点电荷dg。假定|r一r"|是观察点r和一个增量电荷位置r"之间的距离,与这个增置电荷相关的电位可由(4.4.1)式给出(2) do(r,r)=^TEl在笛一卡儿坐标系中,式中的Ir-r'/=V(-')"+(9-9')+(2-2)注意到式(2)是两组笛卡儿坐标的函数:要求电位值的点(观察点)r的坐标(,9,2)和增量电荷所在点(源点))r"处的坐标(",9",")。依照叠加原理,保持观察点(3,3,2)固定,通过把所有微分电位相加,我们可以得到所有微分电荷之和在观察点产生的总电位。对所有微分体积单元求总和变成对坐标(",3",")求体积分。00-1. 2(3)这就是对子电准静态也位的重叠积分。计算电位要求完成个三重积分。可借功于计算机,甚至可编程序计算器来完成,这是“个直截了当的过程。几乎没有一个三重积分可以毫不费力地用解析方法求出的例子。.79:

式(3)也有特殊的表达代。适用电荷分布限于面分布、线分布或电荷分布是二维的情况。于这些,积分次数减小到二次甚至一次,因而获得解析表达式的难度也就大大减小了。主维的电荷分布可由线成片电荷的叠加表示,利用解析地求得的这些电荷分布产生的电位可以使通常在确定三维电荷分布的电位时所要求的数值积分次数减少到二次甚至一次。面电荷密度的蓝叠积分如果电荷密度限制在可以用厚度^很小的表t-rt面描述的区域,那未式(3)的三重积分中的重积bV分一般可以求出来。情况如图4.5.2所示,这时到观察点的距离要比电荷分布面的厚度大得多。由于式(3)的积分是在这个厚度A_上进行的,所以源点和观察点之间的距离lr-rl没有多少变化。因此,当用来表示垂直于该处电街分布面的坐图4.5.2位于电荷无在观费点标时,一般的重叠积分式(3)可简化为上产的电0(r)=[A, 4元e0lr-rlp(r'ds(4)根据定义,对的积分是面电荷密度。因此,式(4)成为造用于该处电荷分布可模拟为在一个面上的重叠积分形式。(r)(r)=(5) J4reolr-r以下例子说明这个积分的应用。例4.5.1均匀带电圆盘的电位图4.5.3所示的圆盘,有半径R,带有均匀面电荷密度g%。以下步骤可得出圆摄轴线上的电位和电场。在半径为P,角度为(在圆柱坐标系中)处的点r与圆盘轴上(z轴)点r之间的距离|r一r"|可给出为=2m2+2(6)1极据上式,式(5)可表示成以下汉重积分p'dp'de'0-.S.p12(7)%N+2-[2l)式中≥既可以总正值,如图4.5.3的情况,也可以为负pdd值。注意这些正负值的点位于这个圆盘的两边。Lr-r轴向电场强度可以通过对式(7)在轴方向求梯度得到。adE,=-WR+2-12l)2图4.5.3一个均勾猎电随盘并带有用来求沿:轴(8)-2;(/R+1)上电位的坐标系.80
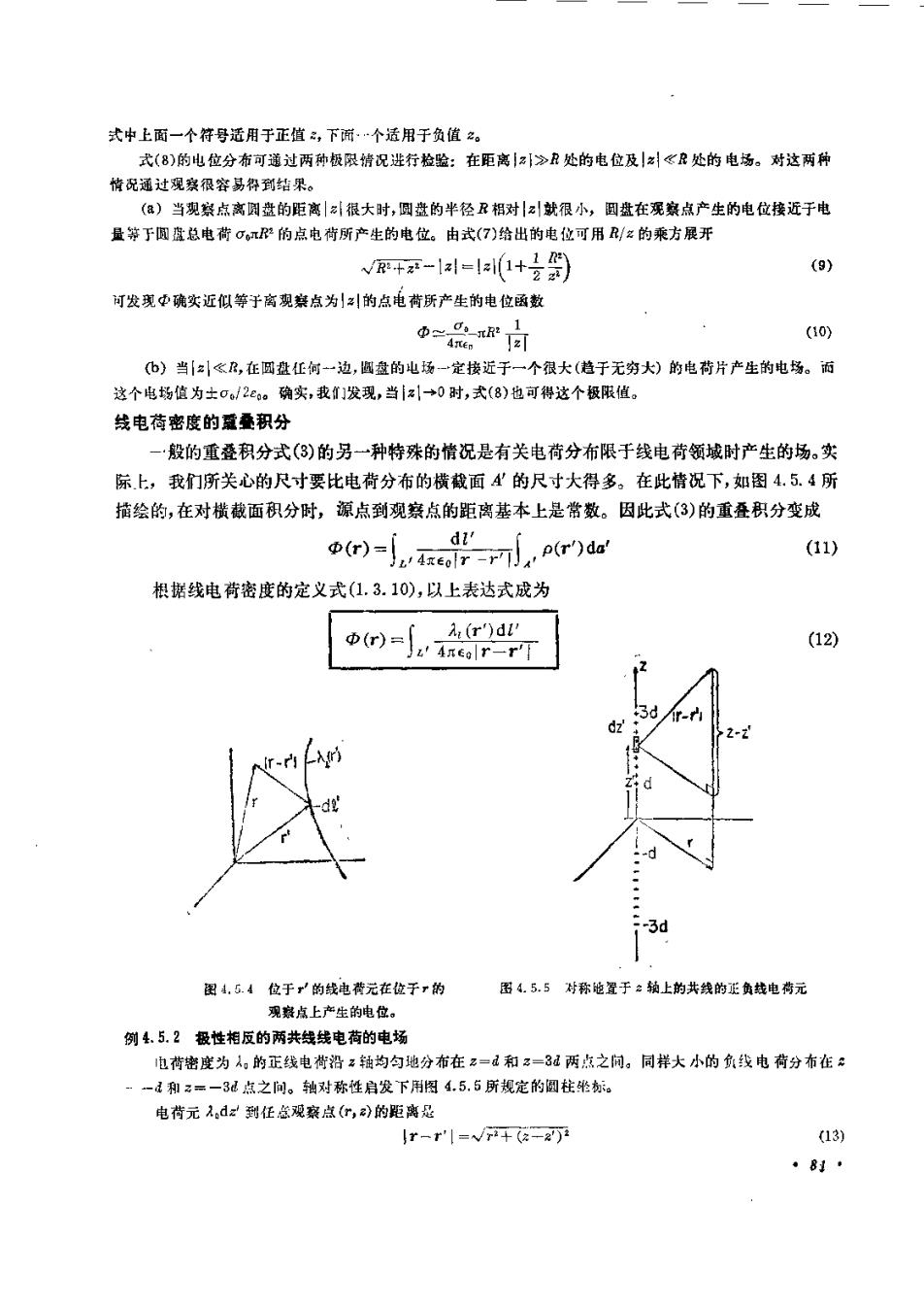
式中上面一个符号适用于正值2,下面个适用于负值2。式(8)的电位分布可通过两种极限情况进行检验:在距离|2[》R处的电位及|2|R处的电场。对这两种情况通过观察很容易符到果。(a)当观察点离圆盘的距离|很大时,圆盘的半径R相对z就很小,圆盘在观察点产生的电位接近于电量等于圆盘总电荷Cg元R的点电荷所产生的电位。由式(7)给出的电位可用R/z的乘方展开VR+2-1a-1a1(1+%)(9) 可发现中确实近似等于离观案点为12的点电荷所产生的电位函数(10)(b)当[2]≤B,在圆盘任何一边,圆盘的场定接近于一个很大(趋于无穷大)的电荷片产生的电场。而这个电场值为±00/2e。确实,我们发现,当[z1→0时,式(8)也可得这个极限值。线电荷密度的盈叠积分般的重叠积分式(3)的另一种特殊的情况是有关电荷分布限于线电荷领域时产生的场。实际上,我们所关心的尺寸要比电荷分布的横截面4'的尺寸大得多。在此情况下,如图4.5.4所描绘的,在对横截面积分时,源点到观察点的距离基本上是常数。因此式(3)的重叠积分变成()-1,-, (r)da(11)根据线电荷密度的定义式(1.3.10),以上表达式成为A(r)dl'0(r)=J,Axlr=r)(12)图4.5.4位于的线电微元在位于^的图4.5.5对称跑置于≥轴上的共线的延负线电荐元观察点上产生的电位。例4.5.2极性相反的两共线线电荷的电场电荷密度为。的正线电荷沿≥轴均勾地分布在 za和z=3&两点之间。同样大小的负线电荷分布在:元和z=—30点之间。轴对称性启发下用图4.5.5所规定的圆柱验称。电荷元 .dz 到任总观察点(r,a)的距离是[r-r'[=Nr+(a-2)(13)81