
为了求出内部区城的@,积分先是在球外区成进行,定处式(24)的值)然后选入半径为T的球内区裁可得(() -4-p(R)+%(r-r)(25)在电荷分布区的外部≥R处,电位民有点电荷的库仑电位形式(26) 注意4是净分布电荷。二维无旋场的形象化一般来说,等位面都是三维的表面。因此,任何恒定电位的二维图形都是这些等位面与某个给定平面的交线。如果电位的依从关系是二维函数,那未等位面就是柱形。例如式(18)表示的二维电位,其等位面具有如图4.1.3所示的双曲线截面的柱面我们复习这些几何概念是因为我们现在介绍一种有助于描绘二维场的不同观点。在画出的三维图形中,第三维用作表示电位@的幅度。这种图如图4.1.4所示,图中以式(18)的电位作为例子。三维图象的底面是-平面,而垂直的那一维坐标代表电位。恒定电位的等位线用恒定商度的线表示。Sr-V图4. 1.4以三继形式表示的式(18)和图 4,1.3 的二维电位,乘直坐标代表电位,类似于一张向上瓷低的潮紧的蘑膜。等位线族是薄跟表面一定高度的等高线族图4.1.4的表面可以看作是一张仲展在位于感兴趣区或周界的支架上的薄膜,这些支架随若边界电位的变化而成正比地抬高或降低。根据梯度的定义式(8),电场强度线总是沿着这个表面坡度最陡的下降轮廓线上。在人们的心目中,等位面是最有意义的,它能把二维电位画成好象一张等高线图,而电场强度线好象水从山上流下形成的水流线。4.2泊松方程给定E是无旋的,即式(4.0.1),并给定高斯定律式(4.0.2)中的电荷密度,那末电场强度的:73

分布又是怎样的呢?由4.1节我们知道,通过用标量电位@表示矢量E。E--O这两个方程中的第一个方程同样可以得到满足。也就是说,由于引人了这种关系,式(4.0.1)已经被积分。在把式(4.0.1)积分后,我们把它放一下,集中解决第二个电准静态方程,即高斯定律。将式(1)代入高斯定律式(1.0.2),给出V.0--PE上式等同于70=-(2) 给定了方程右边的电荷密度,对这个标量的泊松方程进行积分,就是本章剩下的任务。类似于电路理论中的常微分方程,方程右边的电荷密度就是“激励函数”,在方程左边的是由式(2)的第二种形式表示的算子,称为Φ的拉普拉新。在笛卡儿坐标系中,由散度和梯度算子的表达式,即由式(2.1.5)和式(4.1.12)可得++--℃(3)+圆柱坐标系和球面坐标系的拉普拉新算子将在习题中求得,并汇集在本教科书最后的表!中。在笛卡儿坐标系中,这种算于表达式中的导数具有常系数。而在另外两种坐标系中,有些系数是随着空间变化的。注意在式(3)中,时间并不作为一个独立的变最出现。因此,求解一个随时间变化的电荷分布p(r,t)在时刻t。的准静态电场的数学问题与求解不随时间变化的电荷分布p(r)的静电场问题是相同的,只是p(r)等于p(r,t=to),即随时间变化的电荷分布在特定时刻t。时的值。在电荷分布已经给定的问题中,求解准静态场的值就等于求解一系列我们感兴趣时刻的不同电荷分布情况下的静态场问题。这里,我们强调这点,是为了说明静电场的求解比人们预先设想的具有更广泛的应用:每个静电场的解表示在一个特定时刻拍的一张“快照”。说了这么多,我们不需要电荷密度和电场的明显时间依从关系,而是说,只是在为了清楚有此要求时,应该这样做。4.3叠加原理正如式(4.2.3)用笛卡儿坐标系举例说明的那样,泊松方程是联系电位@(r)和电荷分布p(r)的线性二阶微分方程。所调“线性”是指微分方程中各导数的系数不是应变量Φ的函数。泊松方程是线性的一个重要推论是Φ(r)服从叠加原理。认识到这与电路理论中线性常微分方程服从叠加原理的相似之处是很有帮助的。叠加原理可以说明如下。考虑两个不同空间分布的电荷密度p.(r)和ps(r)。这两个电荷分布也许归属于不同的区域,或占有同一个区域。假设我们已分别地求得相应的电荷分布分别为p,和Ps并满足泊松方74

程(4.2.3)的电位中。和中。由定义V'0.(r)= -p.(r)(i)1'0)(r)=-h(n)(2) 把这两式相加,得(3)"0.(r)-V'D.(r)=-[p.(r)+ p(r))内为拉普拉新运算中要求的导数,例如式(4.2.3)中二阶导数,无论是先对各个电位求导然后相加,还是先把电位相加再进行求导,其结果是相同的,因此式(3)还可写为,(r)+(r)]=-1p.(r)+p(r))(4)由式(1)、(2)和(4)得登加原理的数学表达式。即,如果.o.(5)p0那末(6)parpb-ΦlΦ由电荷分布的叠加而产生的电位分布,等于与个别分布相关的电位之和。4.4与电荷奇异性相关的电场本节的任务至少有三项。第一,举例说明4.3节的叠加概念。第二,开始处理不是非常对称的电场,用图形表示这类电场时,电位是非常有用的,因此我们继续深入讨论用图形表示电位和出场分希的方法。最后,研究出的电位函数在以后各章中还会多次出现。象这节描述的,泊松方程在整个空间的解将证明是在没有电荷的子域中拉普拉斯方程的解。因此,在拉普拉斯方程起重要作的第 5章中,还将用第二种观点来讨论。首先,考虑与位于球坐标原点的点电荷相关的电位。电场可以应用1.3节中的高斯定律的积分形式式(1.3.12)求得。根据电位的定义,即式(4.1.4),可得点电荷的电位为(1)@=Ane这个对于三维泊松方程的“冲击响应”是公式推导和问题求解的出发点,是值得记住的。下面考总与分别位于z轴上a/2和一d/2处的一个正电荷和一个负电荷相关的电场,其图形e示于图4.4.1。式(1)中,是观察点与电荷之间的标量距离。用P表示观察点的位置,在图 4. 4. 1中这两个距离用r和r来表示。根据式(1)和图44.12轴上大小相等,符号相反的两个点电存75
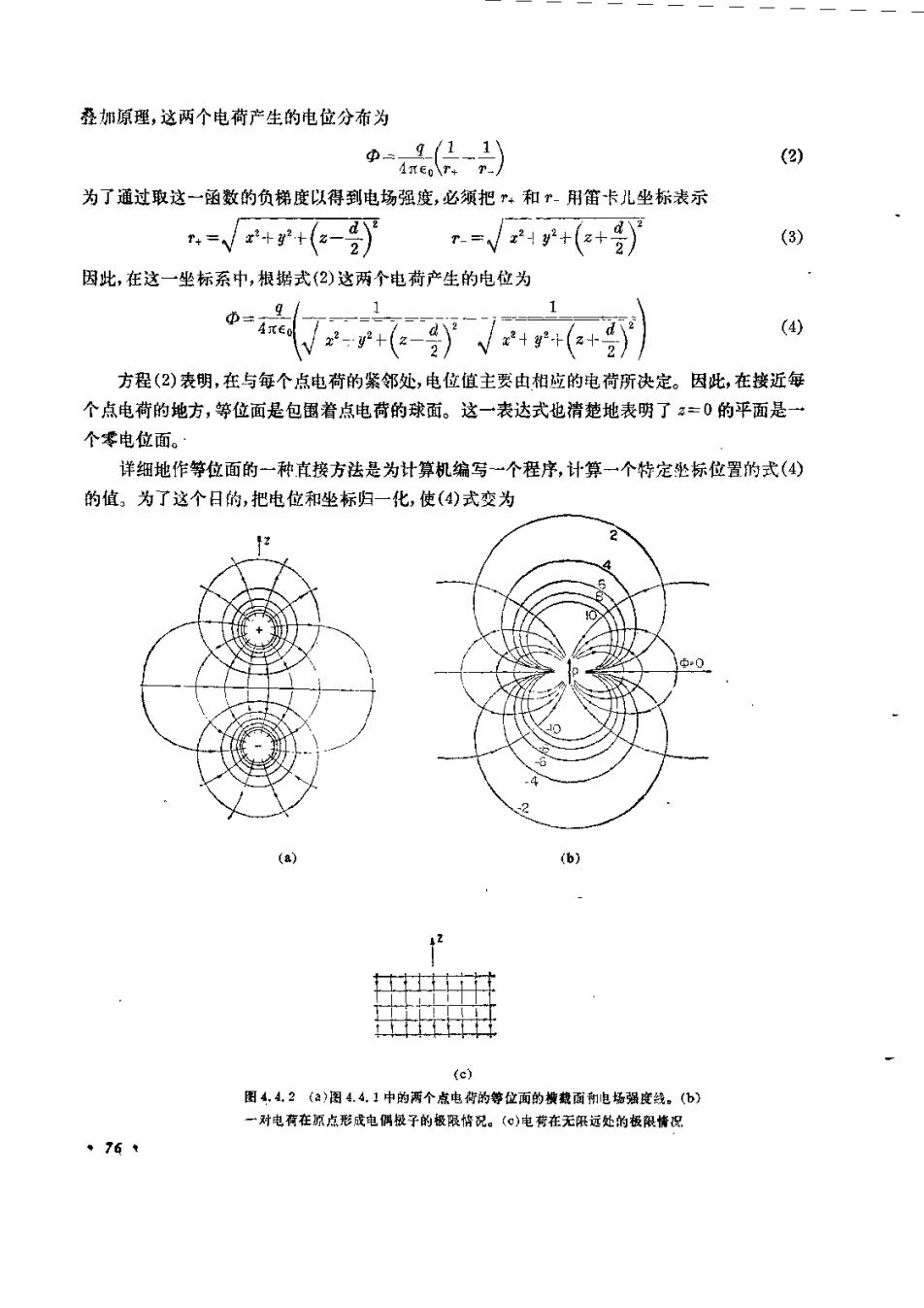
叠加原理,这两个电荷产生的电位分布为/11)(2) D-A()为了通过取这一函数的负梯度以得到电场强度,必须把1、和"-用笛卡儿坐标表示r=/249+(e+号)=/2+9+(c-%)(3)因此,在这一坐标系中,根据式(2)这两个电荷产生的电位为D=(4)Ve-+(s-号)e+g+(a+方程(2)表朗,在与每个点电荷的紧邻处,电位值主要由相应的电荷所决定。因此,在接近每个点电荷的地方,等位面是包围着点电荷的球面。这一表达式也清楚地表明了“=0 的平面是一个零电位面。详细地作等位面的一种直接方法是为计算机编写一个程序,计算一个特定丛标位置的式(4)的值。为了这个日的,把电位和坐标归一化,使(4)式变为c)图4.4,2(2)图4.4. 1中的两个点电荷的等位面的横裁面新电场强度线。(b)一对电荷在原点形成电偶极子的极限情况。(e)电在无限远处的板限情况76

(5)D+(-)()是方便的。式中4一号→鱼(/4ade)通过对不同的坐标位置求Φ值的方法,就有可能以多次计算的方式找到给定等位面的坐标位置。图4.4.2a的等位线就是在=0的条件下画出的。当然,等位面实际上是三维的面,它们可以由图示的曲线绕轴旋转得到。出于E等于中梯度的负值,电场强度线是垂直于等位面的。因此,电场强度线能很容易地画出,并在图4.2.2a中用带篇头的曲线表示。位于原点的电偶极子式(2)的一个重要极限相应于远离两个点心荷的观察点来看场的情况。这是一个非常重要的极限,因为符号相反的电荷对是极化了的原子或分子的模型。因此电偶极于将是第 6 章的中心,在那里,我们将讨论可极化物质。正常情况下,取偶极子的极限就是认为当》时,观察点和各电荷的连线基本上平行于『坐标。图4.4.3中表示的图4.4.3远离电偶极子处,从电荷到观察点的射线基本上平行于坐标近似几何关系可引出以下近似(6)T.二r十号coso+r---cos0;由于表达式中第一项比第二项大得多,",和"-的乘幂可以展开成二项展开式(7) (a+b)"=a"+na"-lb+.于=—1,式(2)可近似为9ol...(-2.s..(8)qdcosoT.Eo记着,这一电位是用球坐标描述的。假设要绘制的等位面图形是在某个特定的位置通过“轴。当我们沿+方向移动时,电位的形状将是怎么样呢?式(8)的左边是定值。当0增加时,公式右边的余弦函数减小。因此,要停留在这个等位面上,从原点到它的距离r必须减小。当角度趋向元/2时,余弦值减小到零,很明减,等位而必须趋近原点。等位面和相关的E线示于图4.4.2b中。电偶极子模型可以从数学上确切地定义为,当两个等量异号电荷的量值不断增大而被此间77