表5-2中列举了部分常用弹性元件材料及其机械性能数据。表5-2常用弹性元件材料及其机械性能 bkg/mm)。,或0 (kg/m)材质8 (%)中 (%)89.51738.55C/MaMob15CMaMo90701150110合22CMnsi901045金110901030C-Mnsi结165130935C,MsiA40构10035C-Mn859钢1004008094550C11095940弹5OC-VA13011010130策60Si2Mn5120钢65Mn10072.5不锈钢iC-18Ni95545203、对弹性元件应进行适当的热处理,使其残余应力尽可能小。4、当传感器用于振动参数测量时,为避免产生畸变,弹性元件最低阶的固有频率至少应为被测过程有效最高谐波频率的3~10倍。表5-3列举了几种简单系统的固有频率
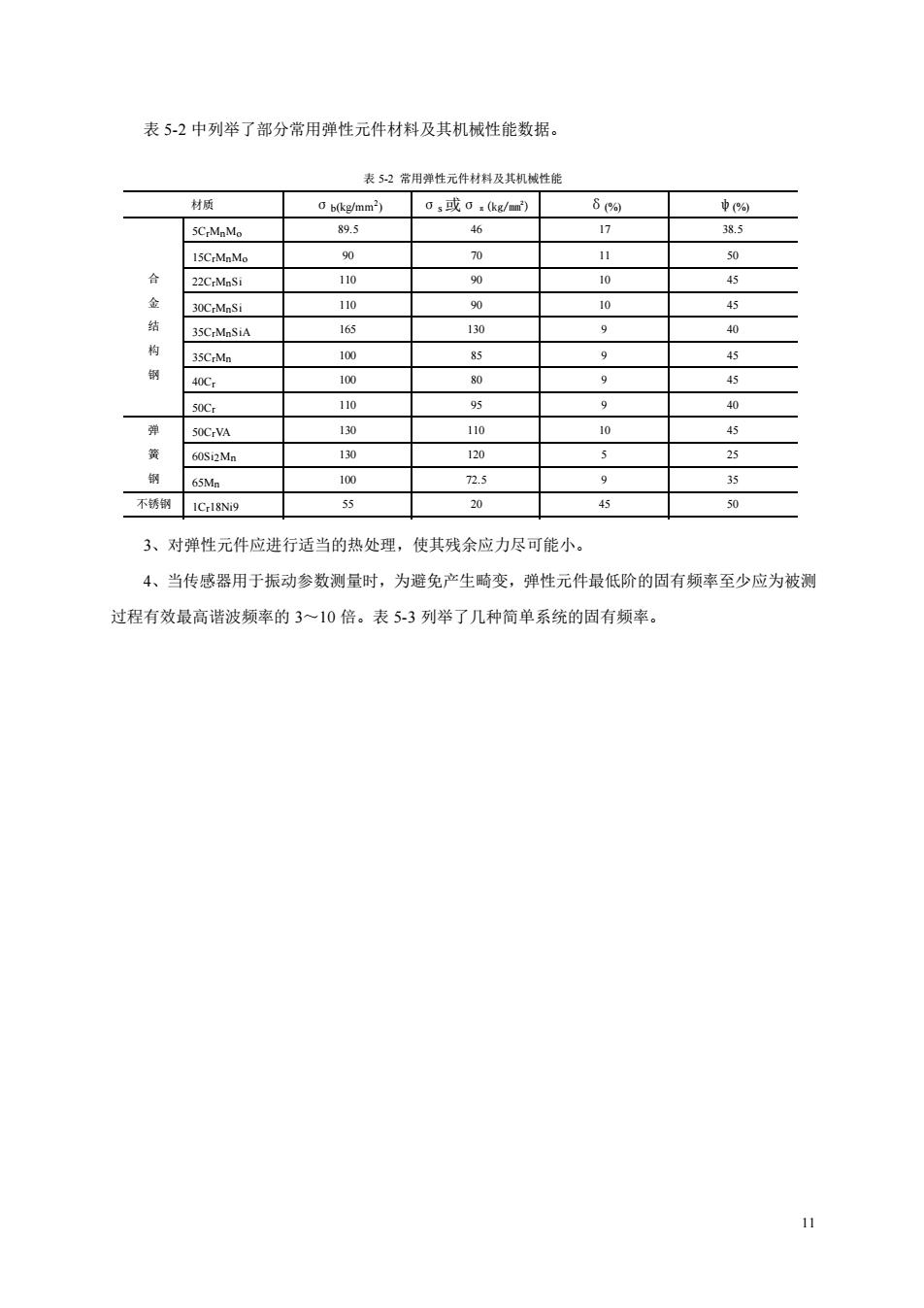
11 表 5-2 中列举了部分常用弹性元件材料及其机械性能数据。 3、对弹性元件应进行适当的热处理,使其残余应力尽可能小。 4、当传感器用于振动参数测量时,为避免产生畸变,弹性元件最低阶的固有频率至少应为被测 过程有效最高谐波频率的 3~10 倍。表 5-3 列举了几种简单系统的固有频率。 表 5-2 常用弹性元件材料及其机械性能 材质 σb(kg/mm2 ) σs 或σπ(kg/mm2 ) δ(%) ψ(%) 合 金 结 构 钢 5CrMnMo 89.5 46 17 38.5 15CrMnMo 90 70 11 50 22CrMnSi 110 90 10 45 30CrMnSi 110 90 10 45 35CrMnSiA 165 130 9 40 35CrMn 100 85 9 45 40Cr 100 80 9 45 50Cr 110 95 9 40 弹 簧 钢 50CrVA 130 110 10 45 60Si2Mn 130 120 5 25 65Mn 100 72.5 9 35 不锈钢 1Cr18Ni9 55 20 45 50 炭素钢 45 61 36 16 40 其它 铍青铜 95 σπ=25 12 — 硬铝 LY12 47 34 17 —
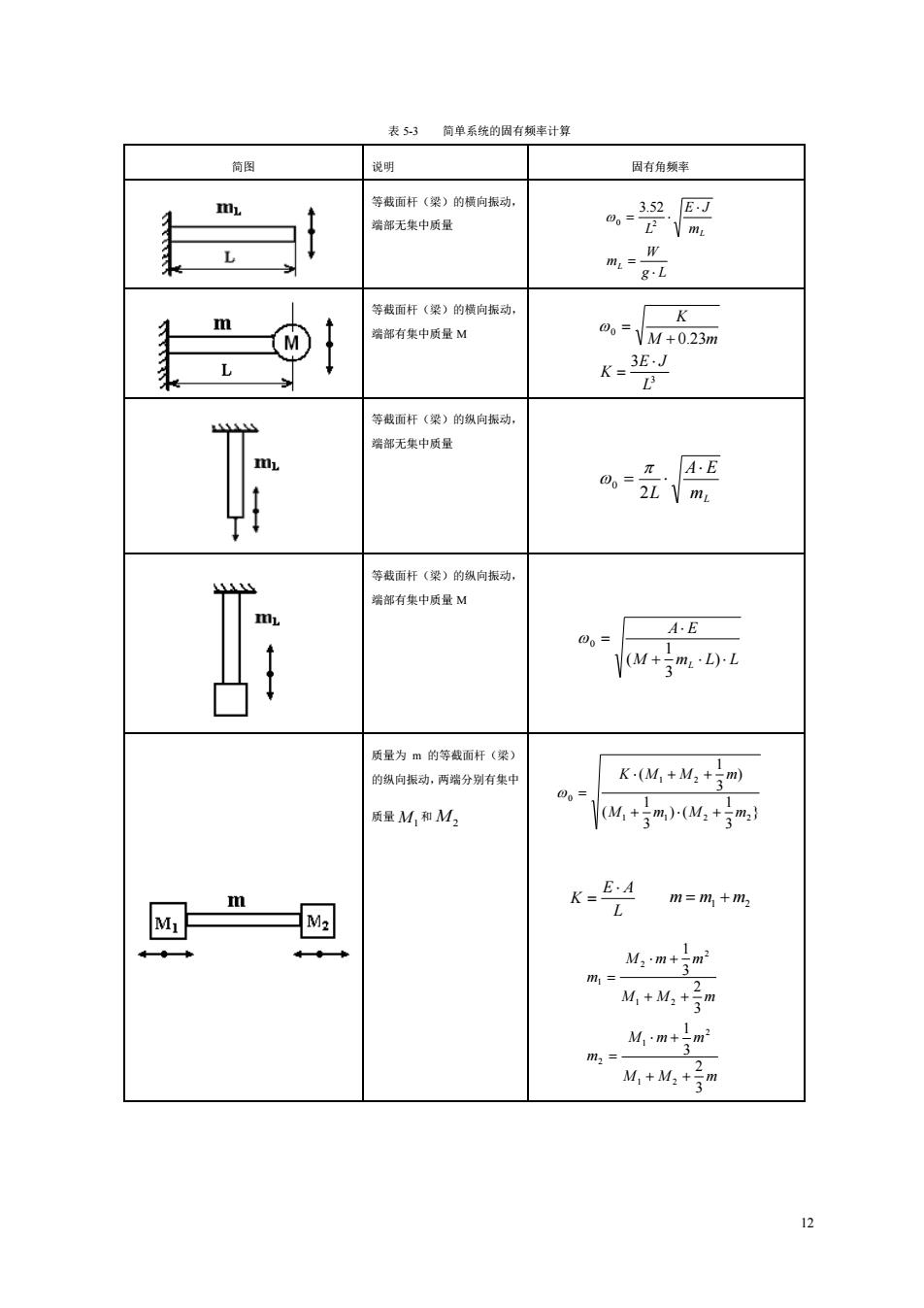
表5-3简单系统的周有频率计算说明固有角辨率简图等截面杆(梁)的横向振动,学my端部无集中质量"兰等载面杆(梁)的横向振动,Km=M+0.23m端部有集中质量MK-T等截面杆(梁)的纵向振动,端部无集中质量my羽等面杆(染)的纵向振动,端部有集中质量MmyA.E1Vm+gm-L)L质量为m的等截面杆(染)K (M +M, +m)的纵向振动,两端分别有集中(M.+m)(M,+gm)质量M,和M,K=E.Am=m,+m,MM.M-m+jmM.+M,+mM.m+/mM.+M,+=m1
12 表 5-3 简单系统的固有频率计算 简图 说明 固有角频率 等截面杆(梁)的横向振动, 端部无集中质量 g L W m m E J L L L = = 0 2 3.52 等截面杆(梁)的横向振动, 端部有集中质量 M 3 0 3 0.23 L E J K M m K = + = 等截面杆(梁)的纵向振动, 端部无集中质量 mL A E L = 2 0 等截面杆(梁)的纵向振动, 端部有集中质量 M M m L L A E L + = ) 3 1 ( 0 质量为 m 的等截面杆(梁) 的纵向振动,两端分别有集中 质量 M1 和 M2 } 3 1 ) ( 3 1 ( ) 3 1 ( 1 1 2 2 1 2 0 M m M m K M M m + + + + = L E A K = m = m1 + m2 M M m M m m m M M m M m m m 3 2 3 1 3 2 3 1 1 2 2 1 2 1 2 2 2 1 + + + = + + + =
固有角额率悦明转动惯量为1,的轴的扭转振动,端部有转动K00惯量为1的集中质量1+7GJ等截面环的径向振动周边固定的圆形薄板振动0 = 1021. Kr2msE.hK= 12(1-μ)主L一杆(梁)的长度,cm:一半径,cm:A一杆(梁)的横截面积,cm2:h一薄板厚度,cm:W一杆(梁)的重量,kgfJ一截面惯性矩,cm;E一弹性摸量,kgf/cm2:G一剪切弹性摸量,kgf/cm2+μ一波桑系数:I、l,一转动惯量,kgf.cm-52:K一刚性系数:M、m一质量,kg?s°/cmtg一重力加速度,cm/s2:m,一单位长度的质量,kgf-s2/cm2:m,一单位面的质量,kgf.5°/cml:my一单位体积的质量,kgf-s/cm:mm,一节点两边杆的质量,kgf-s/cm(四)常见测力传感器的弹性元件从工作原理上讲,凡是能传递应变能的弹性体都可作为传感器的弹性元件,因此弹性元件会有各式各样的结构,应根据实际需要进行设计或选用。表5-4列举了一些常见弹性元件的主体结构、应变和挠度的计算公式
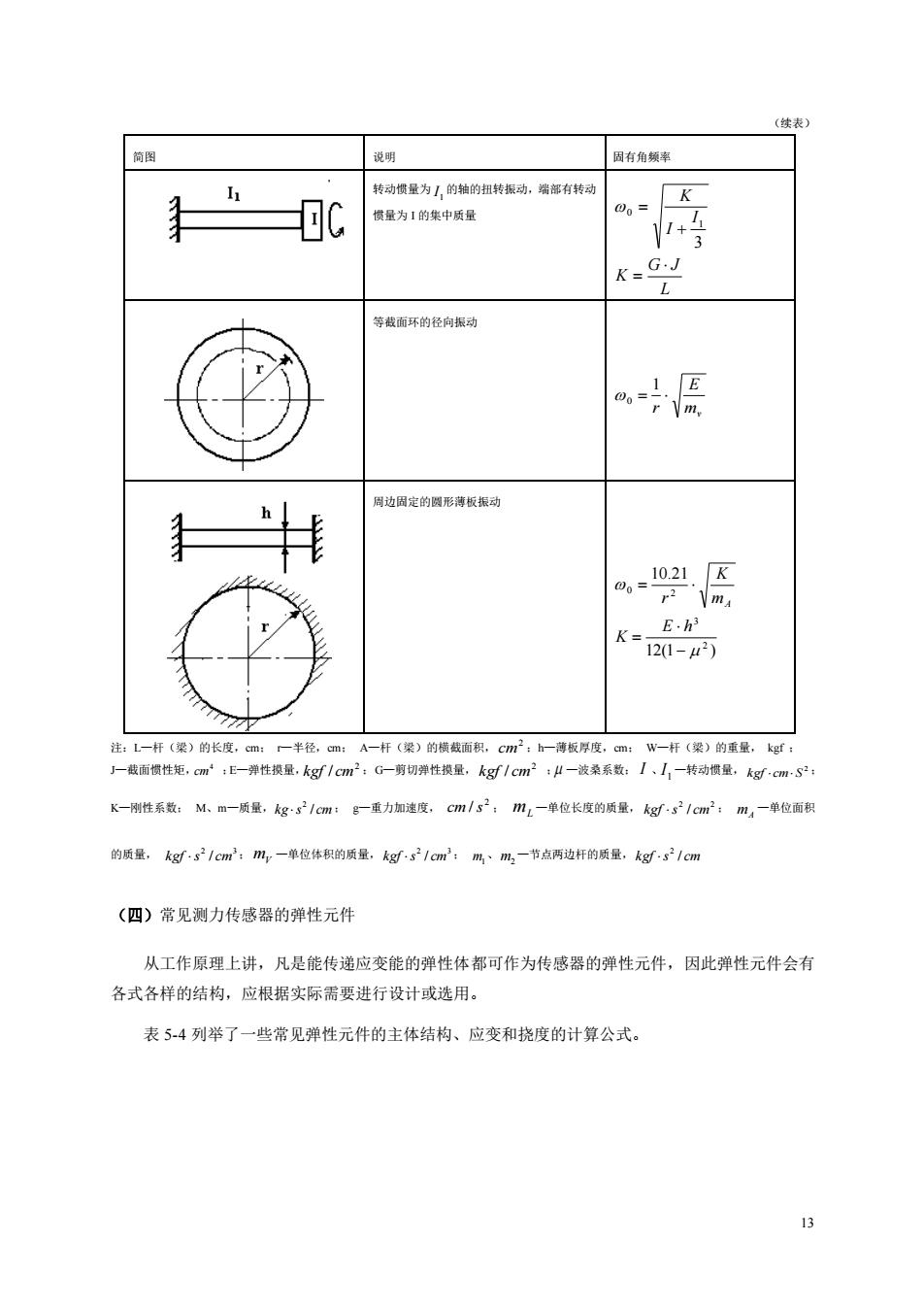
13 (续表) 简图 说明 固有角频率 转动惯量为 1 I 的轴的扭转振动,端部有转动 惯量为 I 的集中质量 L G J K I I K = + = 3 1 0 等截面环的径向振动 mv E r = 1 0 周边固定的圆形薄板振动 12(1 ) 10.21 2 3 0 2 − = = E h K m K r A 注:L—杆(梁)的长度,cm; r—半径,cm; A—杆(梁)的横截面积, 2 cm ;h—薄板厚度,cm; W—杆(梁)的重量, kgf ; J—截面惯性矩, 4 cm ;E—弹性摸量, 2 kgf / cm ;G—剪切弹性摸量, 2 kgf / cm ; —波桑系数; I 、 1 I —转动惯量, 2 kgf cm S ; K—刚性系数; M、m—质量, kg s / cm 2 ; g—重力加速度, 2 cm / s ; mL —单位长度的质量, 2 2 kgf s / cm ; mA —单位面积 的质量, 2 3 kgf s / cm ; mV —单位体积的质量, 2 3 kgf s / cm ; m1、 m2 —节点两边杆的质量, kgf s / cm 2 (四)常见测力传感器的弹性元件 从工作原理上讲,凡是能传递应变能的弹性体都可作为传感器的弹性元件,因此弹性元件会有 各式各样的结构,应根据实际需要进行设计或选用。 表 5-4 列举了一些常见弹性元件的主体结构、应变和挠度的计算公式

表5-4常见弹性元件的主体结构、应变和挠度计算十算一作用力%-)一外纵向应变;=-e8。一外横向应变;4-+81一内纵向应变:=-0e8,一内横向应变一总挠度f-4P(号+2%)ab.c.d.e—几何尺寸,见图Eae弹性模量。作用一外纵向应变;_6PR6,一内级向应变;CEae厂一端部揽度;=6zPR?R一平均半径:一厚度 (R/e>5):Eaeα一宽度。P一作用力:6.一外纵向应变:PR(1-2)6,一内纵向应变Eae一径向挠度PRR一平均半径;f =1.79一厚度 (R/e>5);Eae一宽度。P一作用力Ply8。一外纵向应变:4EW+)8;一内纵向应变:一抗弯截面系数。pley4EWg+
14 表 5-4 常见弹性元件的主体结构、应变和挠度计算 序号 结 构 简 图 计 算 公 式 说 明 1 半框架 1) 6 ( 1 = − e c Eae P e 2 1 e = − 1) 6 ( 1 = − + e c Eae P i 2 1 i i = − (3 2 ) 4 3 3 2 d c e b Ea Pc f = + P—作用力; 1 e —外纵向应变; 2 e —外横向应变; 1 i —内纵向应变; 2 i —内横向应变; f—总挠度; a,b,c,d,e—几何尺寸,见图; E—弹性模量。 2 半圆环 2 6 Eae PF e = 2 6 Eae PR i = − 3 3 6 Eae PR f = P—作用力; e —外纵向应变; i —内纵向应变; f—端部挠度; R—平均半径; e—厚度(R/e>5); a—宽度。 3 圆环 ) 2 (1 3 2 = − Eae PR e ) 2 (1 2 = − − Eae PR i 3 3 1.79 Eae PR f = P—作用力; e —外纵向应变; i —内纵向应变; f—径向挠度; R—平均半径; e—厚度(R/e>5); a—宽度。 4 框架 ) 2 2 4 ( ) 2 ( 2 a b EW b P e + = ) 2 2 4 ( ) 2 ( 2 a b EW b P i + = − P—作用力; e —外纵向应变; i —内纵向应变; W—抗弯截面系数