序受力状况按变电桥组合型式测量项目片数状态电桥电桥输出电压特点量尚电桥接法及应变值型式号M2M1M[R2]两处弯曲应变差/R1能实现温度补带,输出信号较弱,2K-&-UUaD但可直按测剪力折L2E=AL1式M2M1M[R2]R110能实现温度补谱,输出信号较强,两处寄单应变差且可直接测剪力RERL2K·E-UUBDE=812能实现温度补偿,输出信号较强,能消除控(压)影响测扭矩,但招转拉K-E-U不能消除弯自影响(压)复扭应变ZR1LI1合作用R6=62
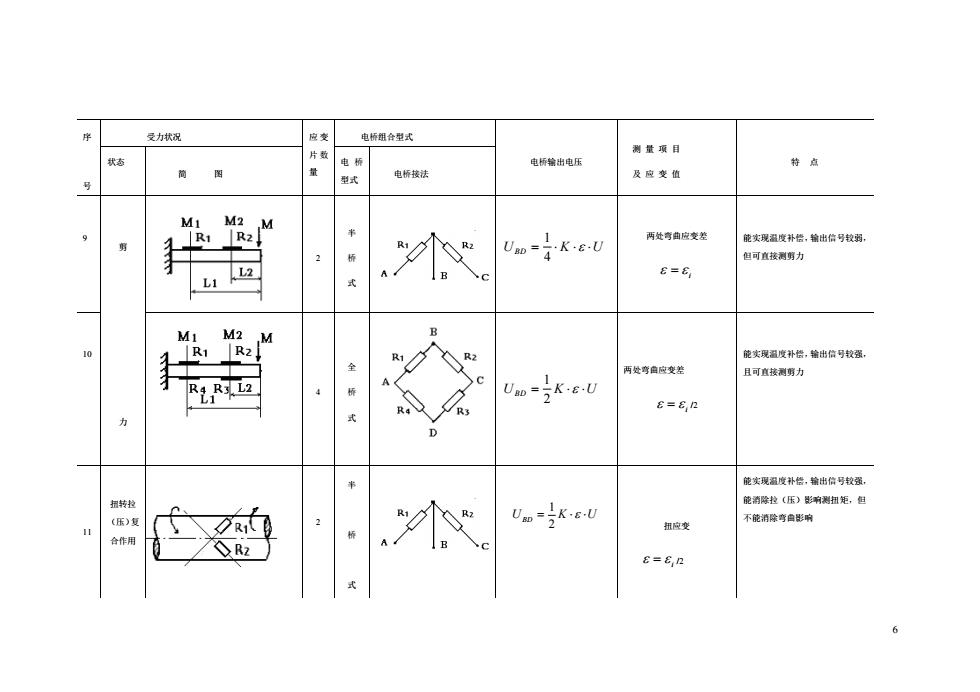
6 序 号 受力状况 应 变 片 数 量 电桥组合型式 电桥输出电压 测 量 项 目 及 应 变 值 状态 特 点 简 图 电 桥 型式 电桥接法 9 剪 力 2 半 桥 式 UBD = K U 4 1 两处弯曲应变差 i = 能实现温度补偿,输出信号较弱, 但可直接测剪力 10 4 全 桥 式 UBD = K U 2 1 两处弯曲应变差 i = /2 能实现温度补偿,输出信号较强, 且可直接测剪力 11 扭转拉 (压)复 合作用 2 半 桥 式 UBD = K U 2 1 扭应变 i = /2 能实现温度补偿,输出信号较强, 能消除拉(压)影响测扭矩,但 不能消除弯曲影响
测量项目dr及应变值S.1能实现温度补(压)倍,输出曲复色RIR4)能消除控(压)R2(B3)影响6=6,4E式注:K一应变片的灵敏系数:U一供桥电压:即所要测量的应变值(机械应变):8试件材料的泊松比工作时的质变念,一应变仪测读的应变值,即指示应变(R)一凡有括号的应变片,是指贴在试件背面相应位置上的应变片
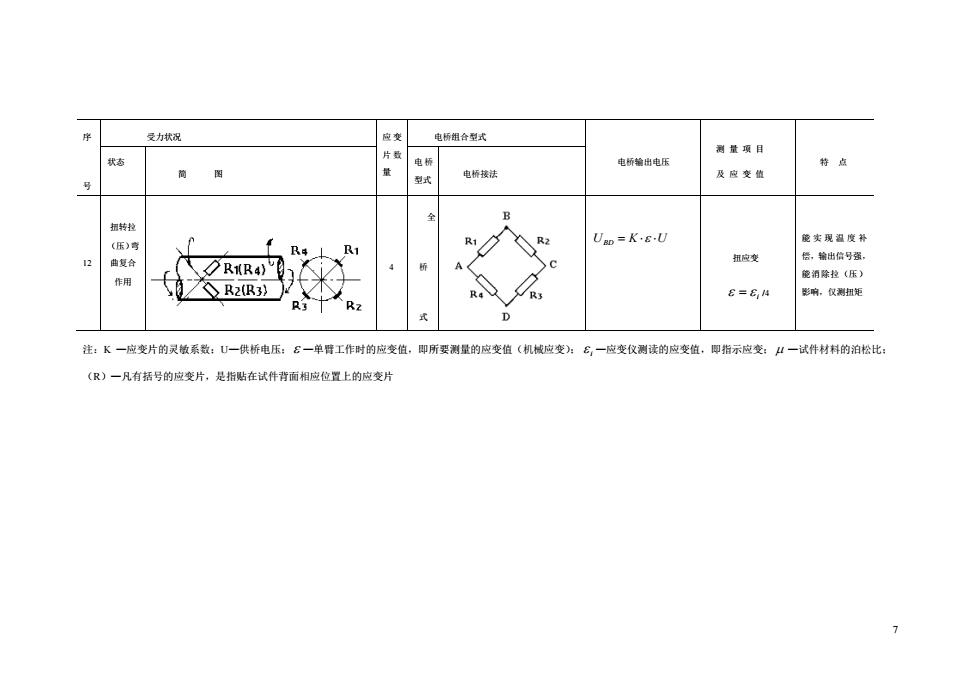
7 注:K —应变片的灵敏系数;U—供桥电压; —单臂工作时的应变值,即所要测量的应变值(机械应变); i —应变仪测读的应变值,即指示应变; —试件材料的泊松比; (R)—凡有括号的应变片,是指贴在试件背面相应位置上的应变片 序 号 受力状况 应 变 片 数 量 电桥组合型式 电桥输出电压 测 量 项 目 及 应 变 值 状态 特 点 简 图 电 桥 型式 电桥接法 12 扭转拉 (压)弯 曲复合 作用 4 全 桥 式 UBD = K U 扭应变 i = /4 能实现温度补 偿,输出信号强, 能消除拉(压) 影响,仅测扭矩

1、拉(压)力的测量如表5-1图1所示,为测量试件所受P力的大小,在试件中间部位沿主应力方向贴一应变片Ri,而在另一块与试件同材质(温度情况也相同)的材料上贴一温度补偿片R2,Ri与R接入相邻桥臂组成测定力P的半桥电路。P力的大小,可按下式计算P-0.A-E-8.A(5-1)式中α一贴片部位的轴向应力A一贴片位置试件的截面积E一试件材料的弹性模量e一贴片部位的应变值,即机械应变。由式(5-1)可知,只要测量出应变值e的大小,便可得到所要测量的力P。为了提高电桥的输出,可将Ri与R2贴于同一试件上,如表5-1图2所示。由于Ri的方向垂直于作用力的方向,因此感受的应变是P力作用方向的-u倍(u为泊松比),这样由Ri、R组成的半桥,其输出为图1的1+μ倍。显然,上述两种布片和接桥方式,不能排除弯曲载荷的影响,为此可采用表5-1图3和图4的方案。可将4枚应变片组成半桥或全桥,其输出为图1的2倍或2(1+μ)倍。2、弯曲载荷的测量如表5-1图7所示,试件在力P作用下,产生弯矩M,在试件上贴一应变片R1,在另一不受力的同质材料上贴一补偿片R2,Ri与R2组成半桥。弯曲载荷M可按下式计算(52)M-W.-W.E.e式中W一试件的抗弯截面系数α一贴片部位的轴向应力E一试件材料的弹性模量ε一所测量的应变值,即机械应变。由式(5-2)可知,只要测量出应变值e的大小,便可得到所要测量的弯曲载荷M。为了提高电桥的输出,将R与R2贴于同一试件上(表5-1图8),也组成半桥,此时电桥的输出增加1倍。更好的是在试件上粘贴4枚应变片,组成全桥(表5-1图9),其输出是单枚应变片工作时的4倍。3、拉(压)弯联合作用时力的测量试件同时受到拉(压)力和弯曲力的联合作用,要求能够单独测量其中一个力而不受另一个力的影响,或同时测量两个力的大小,而互不影响。表5-1图11所示,在试件上粘贴Ri与R2两枚应变片,组成半桥可测量弯曲力P,并且,因拉(压)力影响而产生的电阻变化△R大小相等、符号相同,利用电桥相邻臂的加减特性,可自动抵消,因此在测量弯曲力的同时,不会受到拉(压)力8
8 1、拉(压)力的测量 如表 5-1 图 1 所示,为测量试件所受 P 力的大小,在试件中间部位沿主应力方向贴一应变片 R1, 而在另一块与试件同材质(温度情况也相同)的材料上贴一温度补偿片 R2,R1 与 R2 接入相邻桥臂 组成测定力 P 的半桥电路。 P 力的大小,可按下式计算 式中 —贴片部位的轴向应力 A—贴片位置试件的截面积 E—试件材料的弹性模量 ε—贴片部位的应变值,即机械应变。 由式(5-1)可知,只要测量出应变值ε的大小,便可得到所要测量的力 P。 为了提高电桥的输出,可将 R1 与 R2 贴于同一试件上,如表 5-1 图 2 所示。由于 R1 的方向垂直 于作用力的方向,因此感受的应变是 P 力作用方向的 -μ倍(μ为泊松比),这样由 R1、R2 组成的 半桥,其输出为图 1 的 1+μ倍。 显然,上述两种布片和接桥方式,不能排除弯曲载荷的影响,为此可采用表 5-1 图 3 和图 4 的 方案。可将 4 枚应变片组成半桥或全桥,其输出为图 1 的 2 倍或 2(1+μ)倍。 2、弯曲载荷的测量 如表 5-1 图 7 所示,试件在力 P 作用下,产生弯矩 M,在试件上贴一应变片 R1,在另一不受力 的同质材料上贴一补偿片 R2,R1 与 R2 组成半桥。 弯曲载荷 M 可按下式计算 式中 W—试件的抗弯截面系数 —贴片部位的轴向应力 E—试件材料的弹性模量 ε—所测量的应变值,即机械应变。 由式(5-2)可知,只要测量出应变值ε的大小,便可得到所要测量的弯曲载荷 M。 为了提高电桥的输出,将 R1 与 R2 贴于同一试件上(表 5-1 图 8),也组成半桥,此时电桥的输 出增加 1 倍。更好的是在试件上粘贴 4 枚应变片,组成全桥(表 5-1 图 9),其输出是单枚应变片工 作时的 4 倍。 3、拉(压)弯联合作用时力的测量 试件同时受到拉(压)力和弯曲力的联合作用,要求能够单独测量其中一个力而不受另一个力 的影响,或同时测量两个力的大小,而互不影响。表 5-1 图 11 所示,在试件上粘贴 R1 与 R2 两枚应 变片,组成半桥可测量弯曲力 P,并且,因拉(压)力影响而产生的电阻变化ΔR 大小相等、符号 相同,利用电桥相邻臂的加减特性,可自动抵消,因此在测量弯曲力的同时,不会受到拉(压)力 P = A = E A (5−1) M =W =W E (5−2)

的影响。若要测量拉(压)力,可以再贴两枚应变片Rs与R4于一不受力的同质材料上,如表5-1图13所示,组成半桥或全桥可测量拉(压)力P,同样,利用了电桥的自动加减特性而消除了弯由载荷的影响。4、剪力的测量剪力不能引起应变片阻值的变化,故应变片不能直接LR测量剪应力,但剪力可以引起正应变的变化,而应变片可以测量正应变,所以应变片可以间接测量剪力。8如图5-1所示,在一悬臂梁上作用一力P,则由此力=61)Ma而引起的各截面上的横剪力Q是相等的,即Q=PMf为测量Q,可在距P力作用点位1的截面上,贴一应a变片R,此截面的弯矩M=P·1-Q·,由材料力学知图5-1剪力分析M=E·e·W(E为试件材料的弹性模量,e为该断面上的应变值,W为抗弯截面系数)。因此,M=Q·1=E·8·W,则OE-6-W(5-3)只要用应变片将该截面的应变值测出,即可求出横剪力Q但上述测量方案的缺点是测量结果与力P 的作用点有关。若采用如表 5-1 图 9 的测量方案,在悬臂梁上贴两片应变片Ri与R2,设其距离力P(即等于横剪力Q)的作用点分别为1和12。因为M, = P.l =Q-llM,=P.l,=Q.l,则M-M,=Q(-1)所以M-M,_M-M,Q-1(5-4)-12a又M,=S-EW;M,=8,E-W则
9 的影响。若要测量拉(压)力,可以再贴两枚应变片 R3 与 R4 于一不受力的同质材料上,如表 5-1 图 13 所示,组成半桥或全桥可测量拉(压)力 P,同样,利用了电桥的自动加减特性而消除了弯曲 载荷的影响。 4、剪力的测量 剪力不能引起应变片阻值的变化,故应变片不能直接 测量剪应力,但剪力可以引起正应变的变化,而应变片可 以测量正应变,所以应变片可以间接测量剪力。 如图 5-1 所示,在一悬臂梁上作用一力 P,则由此力 而引起的各截面上的横剪力 Q 是相等的,即 Q=P。 为测量 Q,可在距 P 力作用点位 l 的截面上,贴一应 变片 R,此截面的弯矩 M=P·l=Q·l,由材料力学知, M=E·ε·W(E 为试件材料的弹性模量,ε为该断面上 的应变值,W 为抗弯截面系数)。 因此, M = Q l = E W ,则 (5 − 3) = l E W Q 只要用应变片将该截面的应变值ε测出,即可求出横剪力 Q 。 但上述测量方案的缺点是测量结果与力 P 的作用点有关。若采用如表 5-1 图 9 的测量方案,在悬 臂梁上贴两片应变片 R1 与 R2,设其距离力 P(即等于横剪力 Q)的作用点分别为 l1 和 l2。因为 2 2 2 1 1 1 M P l Q l M P l Q l = = = = 则 ( ) 1 2 1 2 M −M = Q l −l 所以 (5 4) 1 2 1 2 1 2 − − = − − = a M M l l M M Q 又 M1 = 1 EW; M2 = 2 EW 则 图 5-1 剪力分析

O-S.E-W-S,EW.5-S.E-W(55) -12式中E1E2一距P力作用点1和72处断面上的应变值由此可见,Q与P的作用点无关,只要测出e1—e2(两断面处的应变差),便可用求出剪力Q参见表5-1图9、10。5、扭矩的测量由材料力学知:当圆轴受纯扭矩时,主应力的方向与轴线成45°夹角:而互相垂直的两主应力绝对值相等、符号相反,且此绝对值等于轴的横截面上的最大剪应力Tmx,即0, =-03;G, = Tmx如表5-1图13所示,在与轴线成45°的方向上贴一应变片,即可测出此处的应变e。根据广义虎克定律,α=E·e/(1+μ),则此应变片所处横断面上的最大剪应力E.6(5-6)T =0=+而扭矩E-E.WM=TmW,=(5-7)[1+μ8一所测应变值μ一试件材料的箔松比式中E一试件材料的弹性模量,kg/cmW,一抗扭截面系数,cm2在实际应用中,为了增加电桥的输出,一一般粘贴2枚或4枚应变片,组成半桥或全桥测量。参见表5-1图14。(三)弹性元件的设计原则1、输出量(弹性元件的变形)与输入量(被测机械量)之间应保持单值对应的线性关系,因此弹性元件任何截面的应力均不应超过材料的比例极限2、有足够的灵敏度,即弹性元件贴片截面的应力应尽可能选用较大的数值,可取mx=(0.5~0.7)α,(,--材料的比例极限),使截面在最大载荷下产生600~1000微应变之变形。同时尽可能选用。,(或。,材料的弹性极限)较大的材料,这样设计的传感器具有较高的相对测量精度但弹性元件的变形量应在应变片的测量范围之内,且不应超过粘接剂和应变片的应变极限。10
10 (5 5) 1 2 1 2 1 2 − − = − − = E W l l a E W E W Q 式中 ε1、ε2——距 P 力作用点 l1 和 l2 处断面上的应变值 由此可见,Q 与 P 的作用点无关,只要测出ε1—ε2(两断面处的应变差),便可用求出剪力 Q。 参见表 5-1 图 9、10。 5、扭矩的测量 由材料力学知:当圆轴受纯扭矩时,主应力的方向与轴线成 45°夹角;而互相垂直的两主应力, 绝对值相等、符号相反,且此绝对值等于轴的横截面上的最大剪应力τmax,即 1 3 1 max = − ; = 如表 5-1 图 13 所示,在与轴线成 45°的方向上贴一应变片,即可测出此处的应变ε。根据广义 虎克定律,σ=E·ε/(1+μ),则此应变片所处横断面上的最大剪应力 (5 6) 1 max − + = = E 而扭矩 (5 7) 1 max − + k = p = Wp E M W 式中 E—试件材料的弹性模量,kg/cm2 ε—所测应变值 μ—试件材料的箔松比 Wp—抗扭截面系数,cm2 在实际应用中,为了增加电桥的输出,一般粘贴 2 枚或 4 枚应变片,组成半桥或全桥测量。参 见表 5-1 图 14。 (三)弹性元件的设计原则 1、输出量(弹性元件的变形)与输入量(被测机械量)之间应保持单值对应的线性关系,因此 弹性元件任何截面的应力均不应超过材料的比例极限。 2、有足够的灵敏度,即弹性元件贴片截面的应力应尽可能选用较大的数值,可取 max =(0.5~ 0.7) p ( p -材料的比例极限),使截面在最大载荷下产生 600~1000 微应变之变形。同时尽可 能选用 p ,(或 e ,材料的弹性极限)较大的材料,这样设计的传感器具有较高的相对测量精度。 但弹性元件的变形量应在应变片的测量范围之内,且不应超过粘接剂和应变片的应变极限