
第5章品数 定义5.1.3设fA→B,g:C→D,若A=C,B=D且 Vx∈A,有x)=g(x),则称函数f和g相等,记为f=g。 例如,函数f:N→N,x)=x3 函数g:1,2,3→N,g(x)=x3 虽然函数和g有相同的表达式x3,但是它们是两个不 同的函数。 如果把和g看成二元关系, fNXN,用列举法表示为: <0,0>,<1,1>,<2,8>,<3,27>,<4,64>,…} g1,2,3×N,用列举法表示为: <0,0>,<1,1>,<2,8>,<3,27>7 按二元关系相等的条件衡量,它们也是不等的。函 数相等和二元关系相等是一致的
第5章 函数 定义5.1.3 设f:A→B,g:C→D,若A=C,B=D且 xA,有f(x)=g(x),则称函数f和g相等,记为f =g。 例如,函数f:N→N,f(x)= x 3 函数g:1,2,3 →N,g(x)=x 3 虽然函数f和g有相同的表达式x 3,但是它们是两个不 同的函数。 如果把f和g看成二元关系, fN×N,用列举法表示为: 0,0,1,1,2,8,3,27, 4,64, … g1,2,3 ×N,用列举法表示为: 0,0,1,1,2,8,3,27 按二元关系相等的条件衡量,它们也是不等的。函 数相等和二元关系相等是一致的

第5章品数 定义5.1.4设fA→B,若f的值域ranf=B,则称f为满射。 设f是A到B的函数,由定义不难看出,如果yeB,都存 在x∈A,使得x)=y,则f是满射函数。 例如,Aa,b,cd},B=1,2,3},f是由A到B的函数, 定义为:f=<a,1>,<b,1>,<c,3>,<d,2>7 因为ran戶孔A)1,2,3=B,所以是满射。图5.2是f的示 意图。由图5.2可得出如下的结论: 若A、B是有限集,f:A→B 是满射,在的示意图中,B中每 个元素至少是一个有向边的终点 b 且A企B1 图5.2
第5章 函数 定义5.1.4 设f:A→B,若f的值域ran f =B,则称f为满射。 设f是A到B的函数,由定义不难看出,如果yB,都存 在xA,使得f(x)=y,则f是满射函数。 例如,A=a,b,c,d,B=1,2,3,f是由A到B的函数, 定义为:f =a,1,b,1,c,3,d,2 因为ran f=f(A)=1,2,3=B,所以f是满射。图5.2是f的示 意图。由图5.2可得出如下的结论: 若A、B是有限集,f:A→B 是满射,在f的示意图中,B中每 个元素至少是一个有向边的终点 且|A|≥|B|

第5章品数 定义5.1.5设fA→B,若Vyeranf,存在惟一的xeA, 使得x)=y,则称f为单射。 设f是A到B的函数,由定义不难看出,如果对于x∈A, x2∈A,x1)y1,x2)y2。 ①当y2时,一定有x=x2,则是单射函数。 ②当x2时,一定有yy2,则是单射函数。 【例5.5】设fa,b7→2,4,67,定义 f=<a,2>,<b,6>7 函数是否为单射?隄否为满射?
第5章 函数 定义5.1.5 设f:A→B,若yran f,存在惟一的xA, 使得f(x)=y,则称f为单射。 设f是A到B的函数,由定义不难看出,如果对于x1A, x2A,f(x1 )=y1,f(x2 )=y2。 ①当y1 =y2时,一定有x1 =x2,则f是单射函数。 ②当x1≠x2时,一定有y1≠y2,则f是单射函数。 【例5.5】设f:a,b→2,4,6,定义 f =a,2,b,6 函数f是否为单射?f是否为满射?
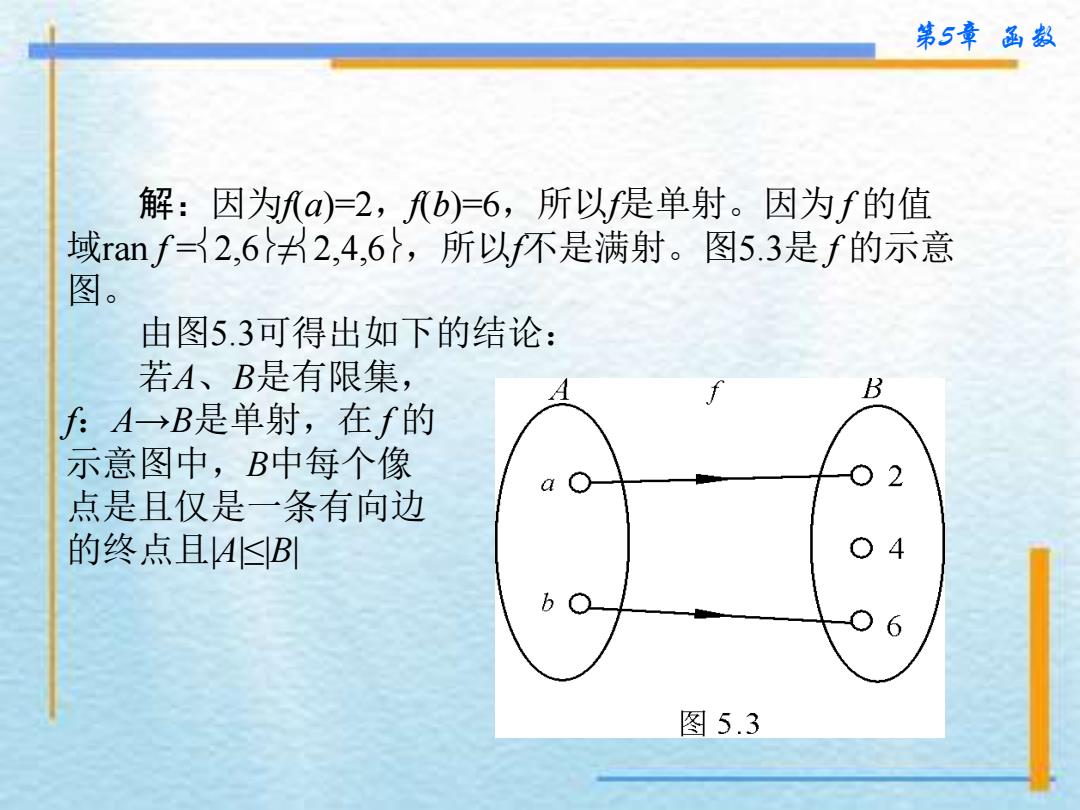
第5章品数 解:因为)=2,b)=6,所以f是单射。因为f的值 域ranf2,6书2,4,67,所以f不是满射。图5.3是f的示意 图。 由图5.3可得出如下的结论: 若A、B是有限集, B f:A→B是单射,在f的 示意图中,B中每个像 点是且仅是一条有向边 的终点且AB 4 b 图5.3
第5章 函数 解:因为f(a)=2,f(b)=6,所以f是单射。因为 f 的值 域ran f =2,6≠2,4,6,所以f不是满射。图5.3是 f 的示意 图。 由图5.3可得出如下的结论: 若A、B是有限集, f:A→B是单射,在 f 的 示意图中,B中每个像 点是且仅是一条有向边 的终点且|A|≤|B|
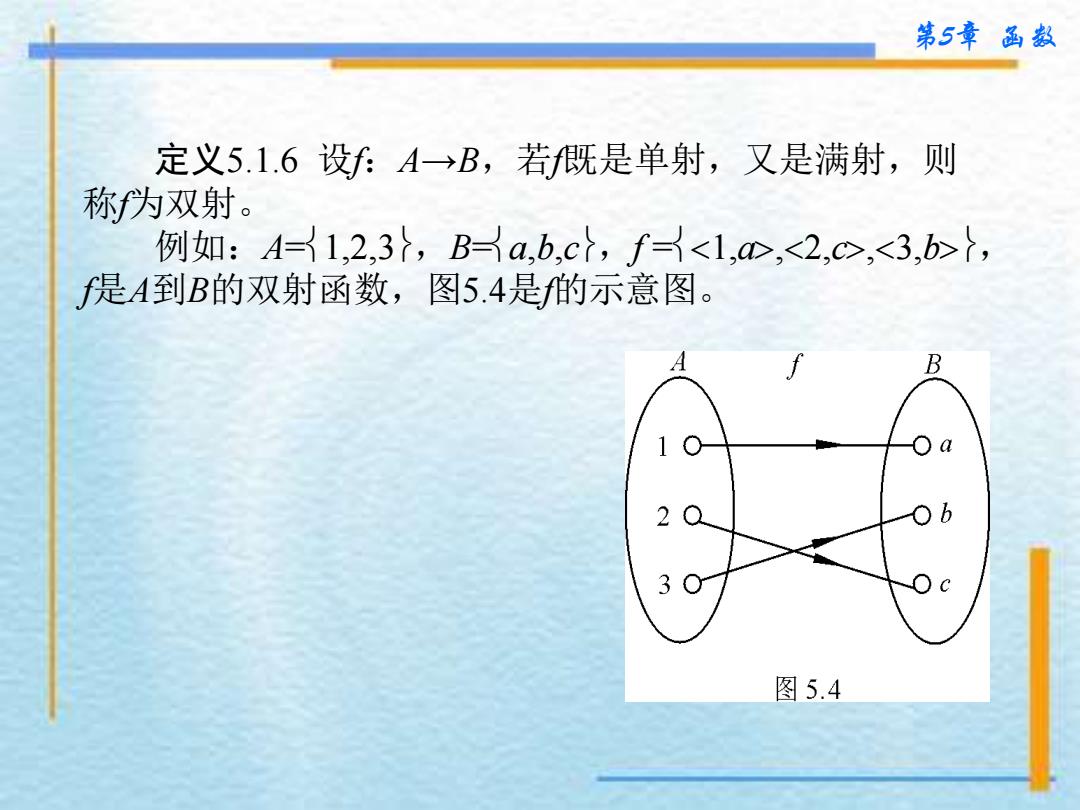
第5章品数 定义5.1.6设fA→B,若f既是单射,又是满射,则 称为双射。 例如:A=1,2,3},Ba,b,c},f<1,心,<2,c②,<3,b>, f是A到B的双射函数,图5.4是的示意图。 B 1 2 b 3 图5.4
第5章 函数 定义5.1.6 设f:A→B,若f既是单射,又是满射,则 称f为双射。 例如:A=1,2,3,B=a,b,c,f =1,a,2,c,3,b, f是A到B的双射函数,图5.4是f的示意图