
严格线性相位定义H(ej9)=H(ejg)lej(2)若蚁2)=一 α2,则称系统H(z)是严格线性相位的。例:单频信号exp(j2k)通过线性相位(LTI)系统的响应T(ejk ) =|H(ej. )lej. (k-a)
严格线性相位定义 j j j ( ) (e ) (e ) e H = H 例: 单频信号exp(j0 k)通过线性相位(LTI)系统的响应 j j j ( ) 0 0 0 {e } (e ) e − = k k T H 若()= − , 则称系统H(z)是严格线性相位的

广义线性相位定义H(ej)= A(2)e-i(2+B)A(2)称为幅度频函数
广义线性相位定义 j j( ) (e ) ( )e − H = A A()称为幅度频函数
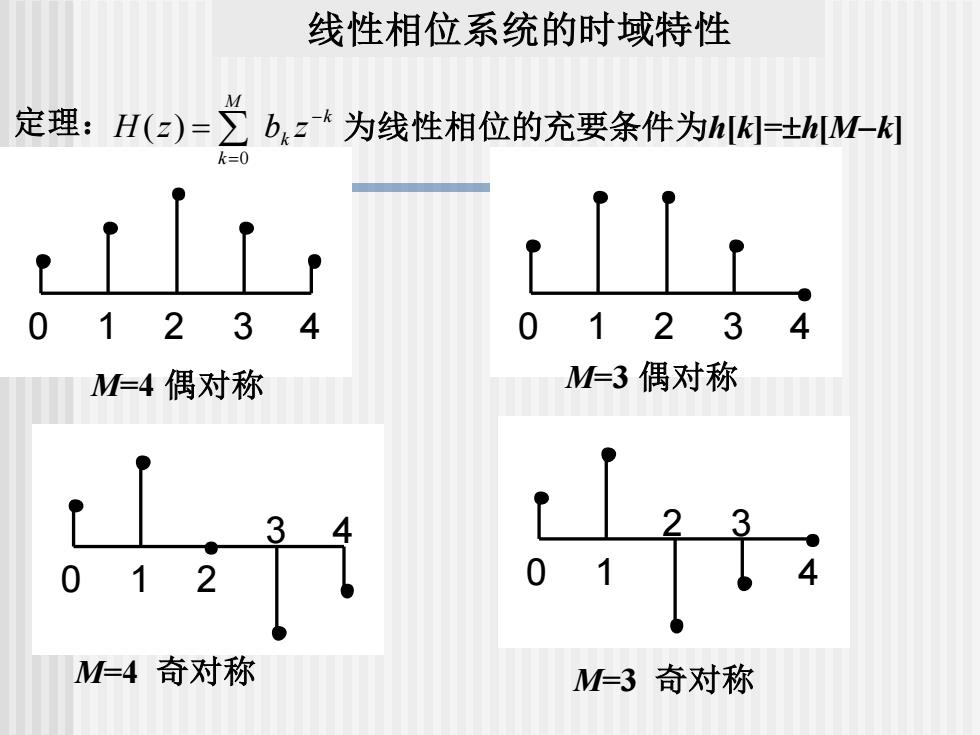
线性相位系统的时域特性M定理:H(z)= bkz-k 为线性相位的充要条件为h[K]=±h[M-k]k=011V02340¥1¥1234-M=3 偶对称M=4 偶对称2334014012M=4奇对称M=3 奇对称
线性相位系统的时域特性 0 1 2 3 4 M=4 偶对称 0 1 2 3 4 M=3 偶对称 0 1 2 3 4 M=4 奇对称 0 1 2 3 4 M=3 奇对称 定理: 为线性相位的充要条件为h[k]=h[M−k] k k M k H z b z − = = 0 ( )