
例8-2:评价代数方法度量风险的准确性 考虑一份到期期限为六个月、执行价格为50的欧式看跌 期权,当前基础资产价格为49,股息收益率为1%,波 动率为20%,分别用数值方法和分解方法计算期权的△、 Y和维加。假设无风险利率为3%。 首先,利用分解法计算欧式看跌期权的△值。 n(49e01o5/50e030)+0.5(0.20)(0.5=-0.00143以及 0.20V5 N(0.00143)=0.5006 △2=-e00100W(-d)=-0.4981
❖ 例8-2: 评价代数方法度量风险的准确性 考虑一份到期期限为六个月、执行价格为50的欧式看跌 期权,当前基础资产价格为49,股息收益率为1%,波 动率为20%,分别用数值方法和分解方法计算期权的∆、 γ和维加。假设无风险利率为3%。 首先,利用分解法计算欧式看跌期权的∆值

。用数值法计算: 令资产价格变化0.1,将BSM看跌期权公式 Pasu Xe N(-d2)-Se "N(-d) 看做OV函数可得△的代数值为 0V(40+0.1)-0V(40-0.1) (49+0.1)-(49-0.1) 2.9702-3.0698 0.2 =-0.4981
❖用数值法计算: 令资产价格变化0.1,将BSM看跌期权公式 看做OV函数可得∆的代数值为
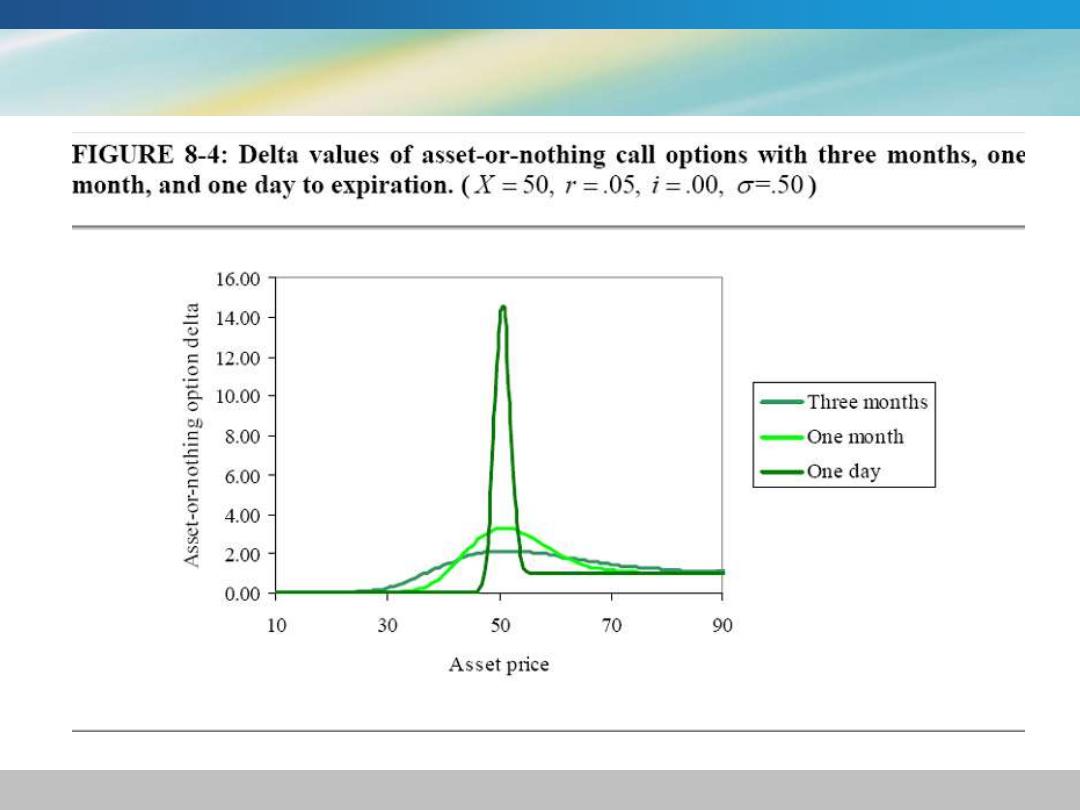
FIGURE 8-4:Delta values of asset-or-nothing call options with three months,one month,and one day to expiration.(X=50,r=.05,i=.00,o=.50) 16.00 elop uondo 14.00 12.00 10.00 Three months 8.00 One month Sulyou-1o-13ssV 6.00 One day 4.00 2.00 0.00 10 30 50 70 90 Asset price

。首先,对于完全亏损的期权,△值接近于0。 其次,完全盈利的期权△值接近于1。 再次,资产或无效看涨期权(不同于标准化看涨 期权)盈亏平衡时的△值远大于1,并随着到期期 限的缩短而增长
❖首先,对于完全亏损的期权,∆值接近于0。 ❖其次,完全盈利的期权∆值接近于1。 ❖再次,资产或无效看涨期权(不同于标准化看涨 期权)盈亏平衡时的∆值远大于1,并随着到期期 限的缩短而增长
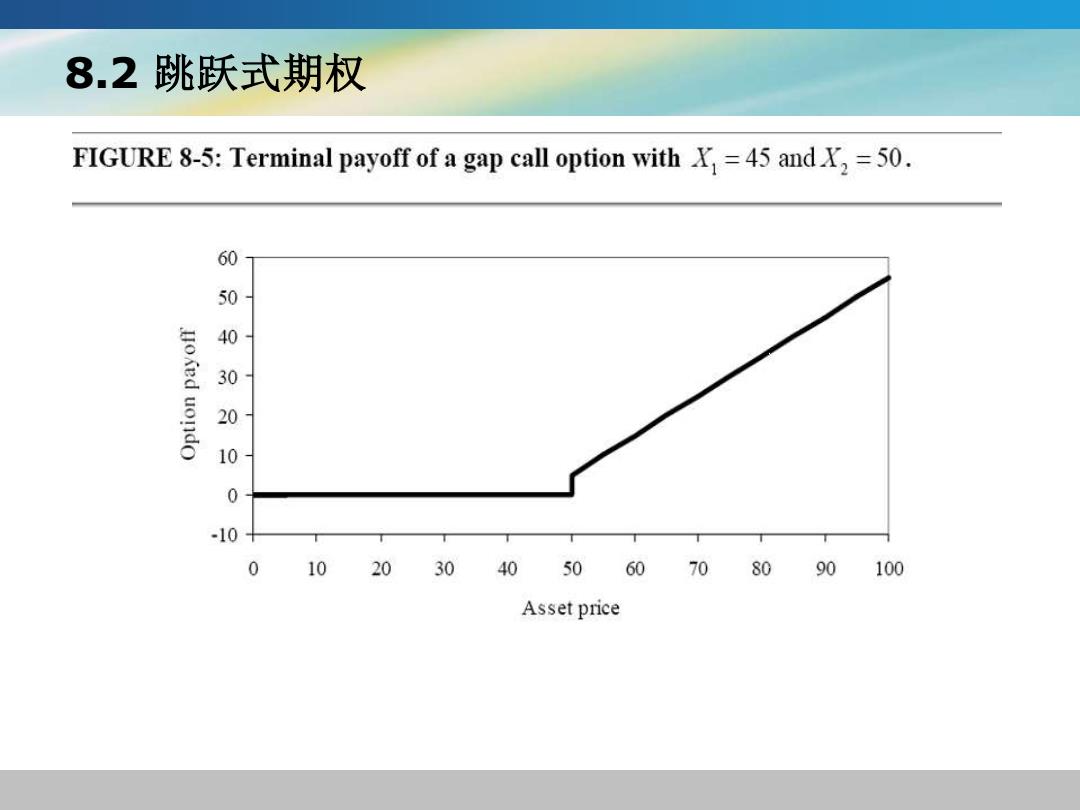
8.2跳跃式期权 FIGURE 8-5:Terminal payoff of a gap call option with X=45 and X,=50. 60 5 uoKed 1 30 1 0 -10 0 102030405060708090100 Asset price
8.2 跳跃式期权