
计算电磁学 (小班研讨课) 966 目录 第十章积分方程 2
2 计算电磁学(小班研讨课) 目 录 第十章 积分方程

10.1积分方程和格林函数 1966 10.1.1积分方程的推导 >有源区域,媒质均匀且各向同性,频域Maxwell7方程 V×E=-joB-M V×H=joD+J (1) V.D=ge V.B=gm Q1:Maxwell7方程组各方程的来历?哪一项是Maxwell的贡献? Q2:自然界不存在磁流和磁荷,采用广义Maxwell7方程组的好孜处? Q3:四个方程是否都是独立的? Q4:直角坐标系下,(1)中有多少个方程,多少个未知数?是否能够求解? 3
3 10.1 积分方程和格林函数 10.1.1 积分方程的推导 ➢ 有源区域,媒质均匀且各向同性,频域Maxwell方程 Q1:Maxwell方程组各方程的来历?哪一项是Maxwell的贡献? Q2:自然界不存在磁流和磁荷,采用广义Maxwell方程组的好处? Q3:四个方程是否都是独立的? Q4:直角坐标系下,(1)中有多少个方程,多少个未知数?是否能够求解? (1) = − − E B M j = + H D J j e = D q m = B q

10.1积分方程和格林函数 >电流(磁流) 连续性定理 V.J=-jage (2) V.M=-j0gm >本构关系 D=8E B=uH (3) >边界条件 -nx(E2-E)=M、 媒质2 nx (H2H=J 777777777777 (4) 媒质1 n.(D2-D)=qe n-(B2-B)=9m Q:理想导体的边界条件是什么? 4
4 (2) 10.1 积分方程和格林函数 ➢ 电流(磁流)连续性定理 e = − J jq m = − M jq ➢ 本构关系 D E = (3) B H = ➢ 边界条件 -n E E M − = ( 2 1 s ) n H H J − = ( 2 1 s ) 媒质 n 2 媒质1 n D D − = ( 2 1 e ) q n B B − = ( 2 1 m ) q (4) Q:理想导体的边界条件是什么?
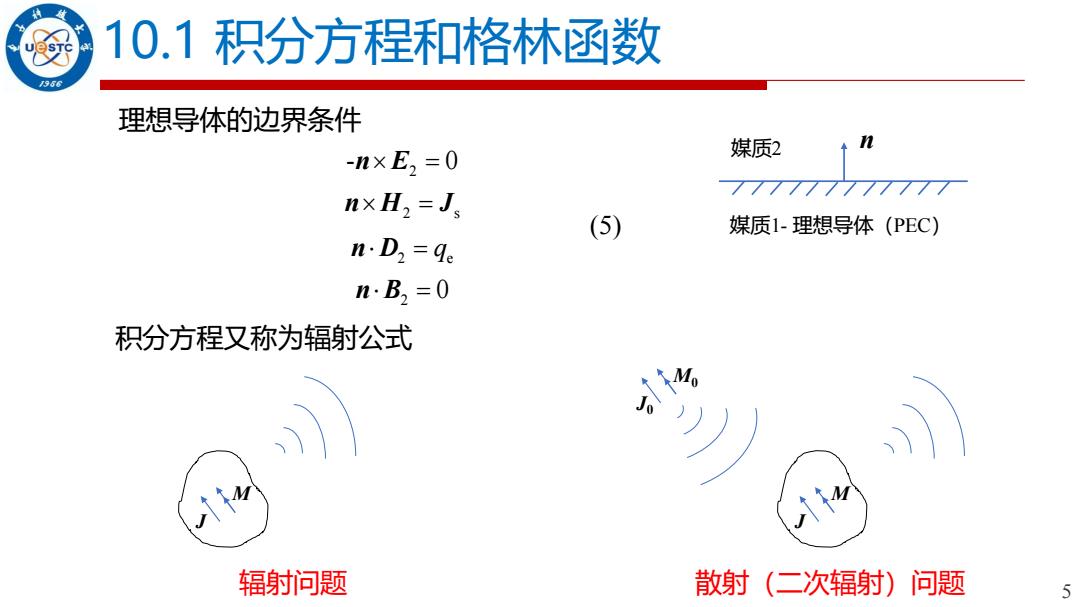
10.1积分方程和格林函数 966 理想导体的边界条件 -n×E,=0 媒质2 n×H2=Js (5) 媒质1-理想导体(PEC) n.D2=ge nB2=0 积分方程又称为辐射公式 辐射问题 散射(二次辐射)问题 5
5 10.1 积分方程和格林函数 媒质 n 2 媒质1- 理想导体(PEC) 2 - 0 n E = n H J =2 s 2 e n D = q 2 n B = 0 理想导体的边界条件 (5) 积分方程又称为辐射公式 辐射问题 J M 散射(二次辐射)问题 J M J0 M0

10.1积分方程和格林函数 966 只考虑电流源和电荷的存在,式(1-1)两边分别取旋度,并代入式(1-2),得 VxVxE-0'ugE=-jouJ (6) 由矢量恒等式VxV×A=V(仅·A)-VA,得 V(7·E)-V2E-k2E=-joJ 其中,波数k=o√G 由式(1-3),有7(V.E)=Vq./s,代入上式得 VE+kE=joul+Vd 再由式(2-1),得到矢量亥姆霍兹方程 VE+kE=jouJ-V(V-J) (7) 10E Q:亥姆霍兹方程和波动方程的区别? 6
6 10.1 积分方程和格林函数 只考虑电流源和电荷的存在,式(1-1)两边分别取旋度,并代入式(1-2),得 2 − = − E E J j (6) 由矢量恒等式 = − A A A ( ) 2 ,得 ( ) 2 2 − − = − E E E J k j 其中,波数 k = 由式(1-3),有 = ( E) qe ,代入上式得 2 2 e j q k + = + E E J 再由式(2-1),得到矢量亥姆霍兹方程 ( ) 2 2 j j k + = − J E E J (7) Q:亥姆霍兹方程和波动方程的区别?