
计算电磁学(小班研讨课 ) 956 目 录 第6章时域有限差分法Ⅲ 6.4应用举例(1) 2
2 计算电磁学(小班研讨课) 目 录 第6章 时域有限差分法 III 6.4 应用举例(II)

计算电磁学 第6章时域有限差分法I 应用 3
3 第6章 时域有限差分法 III ——应用 计算电磁学
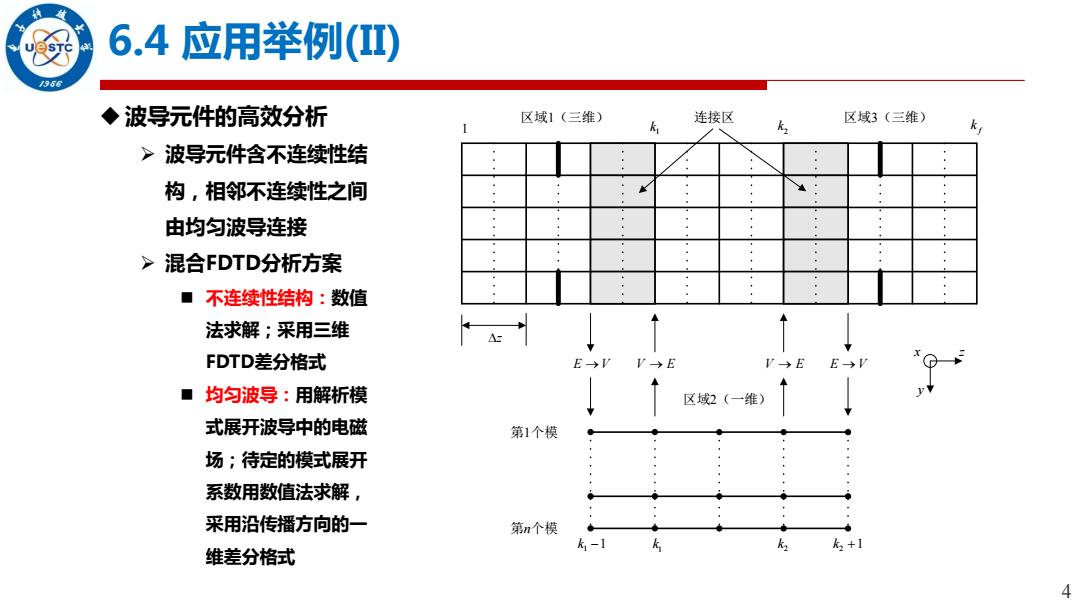
6.4应用举例(I) 966 ◆波导元件的高效分析 区域1(三维) 连接区 区域3(三维) k >波导元件含不连续性结 构,相邻不连续性之间 由均匀波导连接 >混合FDTD分析方案 ■不连续性结构:数值 法求解;采用三维 FDTD差分格式 E→VV→E V→EE→V ■均匀波导:用解析模 ↓↑ 区域2(一维) 式展开波导中的电磁 第1个模 场;待定的模式展开 系数用数值法求解, 采用沿传播方向的一 第n个模 k,+1 维差分格式 4
4 6.4 应用举例(II) 波导元件的高效分析 波导元件含不连续性结 构,相邻不连续性之间 由均匀波导连接 混合FDTD分析方案 不连续性结构:数值 法求解;采用三维 FDTD差分格式 均匀波导:用解析模 式展开波导中的电磁 场;待定的模式展开 系数用数值法求解, 采用沿传播方向的一 维差分格式 区 域 1 ( 三 维 ) z 1 1 k 2 k f k 连接区 区域3 ( 三 维 ) z yx E V V E V E E V 区域2(一维) 第1个模 第n个模 1 k 1 k 1 2 k 2 k 1

6.4应用举例(I) 966 >均匀波导区(区域2:k从k1-1到k2+1) 区域1(三维) 连接区 区域3(三维) k ■横向电磁场分量 (6.103)E,(x,y2,)=∑n(,t)e(x,y) (6.104) H,(x.y,=,t)=>1(=,t)h,(x.y) en和h,是正交归一化的模式本征矢量 ■ 电磁场振幅(等效电压Vn和电流In)与场分布的关系 (6.105) V(,t)=E,(x,y,=,t)-e(x.y)dxdy ↓↑ EVV->E (6.106) I(t)=H,y.t)h(x)dxdy 区域2(一维) 第1个模 S是波导的横截面 ■Vn和ln均满足微分方程 8105-k足,=0 第n个模 0z2c602 k。,是第n个模式的本征值,C0是真空中的波速,fn代表第n个模式在z坐标处的时变振幅 5
5 6.4 应用举例(II) 均匀波导区(区域2:k从 k1-1到k2+1) 横向电磁场分量 (6.103) (6.104) 和 是正交归一化的模式本征矢量 电磁场振幅(等效电压Vn和电流In)与场分布的关系 (6.105) (6.106) S是波导的横截面 Vn和In均满足微分方程 是第n个模式的本征值,C0 是真空中的波速,fn代表第n个模式在z坐标处的时变振幅 区域1(三维) z 1 1 k 2 k f k 连接区 区域3(三维) z yx E V V E V E E V 区域2(一维) 第1个模 第n个模 1 k 1 k 1 2 k 2 k 1 ( , , , ) ( , ) ( , ) t n n n E e x y z t V z t x y ( , , , ) ( , ) ( , ) t n n n H h x y z t I z t x y n e hn ( , ) ( , , , ) ( , )d d n t n S V z t x y z t x y x y E e ( , ) ( , , , ) ( , )d d n t n S I z t x y z t x y x y H h 2 2 2 2 2 2 c 0 1 0 n n n n f f k f z c t cn k
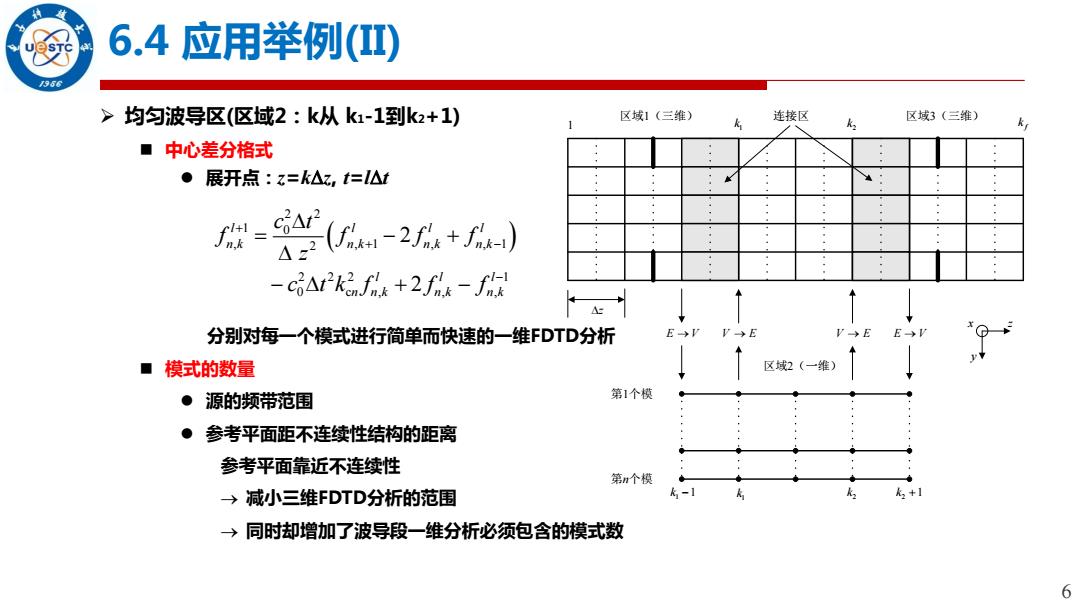
6.4应用举例(I) 966 >均匀波导区(区域2:k从k1-1到k2+1) 区域1(三维) 连接区 区域3(三维) k ■中心差分格式 ●展开点:z=k△z,t仁l△t (fi-2) 43 -c6△tk3nfh+2f品-f 分别对每一个模式进行简单而快速的一维FDTD分析 EVV>E E ■模式的数量 区域2(一维) ●源的频带范围 第1个模 ●参考平面距不连续性结构的距离 参考平面靠近不连续性 第n个模 →减小三维FDTD分析的范围 →同时却增加了波导段一维分析必须包含的模式数 6
6 6.4 应用举例(II) 均匀波导区(区域2:k从 k1-1到k2+1) 中心差分格式 展开点:z=kz, t=lt 分别对每一个模式进行简单而快速的一维FDTD分析 模式的数量 源的频带范围 参考平面距不连续性结构的距离 参考平面靠近不连续性 减小三维FDTD分析的范围 同时却增加了波导段一维分析必须包含的模式数区域1(三维) z 1 1 k 2 k f k 连接区 区域3(三维) z yx E V V E V E E V 区域2(一维) 第1个模 第n个模 1 k 1 k 1 2 k 2 k 1 2 2 1 0 , , 1 , , 1 2 2 2 2 1 0 c , , , 2 2 l l l l n k n k n k n k l l l n n k n k n k c t f f f f z c t k f f f