计算电磁学 (小班研讨课) 966 第8章矩量法基本原理 目录 2
2 计算电磁学(小班研讨课) 目 录 第8章 矩量法基本原理

8.2静电场中的矩量法 8.2.1一维平行板电容器 两板间的电荷密度:p=6(1+4x2) 求解电容器两板间的电位分布。 (1)解析解 解:在区间x∈[0,1]上,电位分布0满足泊松方程 股会+4) 其中,边界条件为0(0)=0(1)=0 可对泊松方程进行两次积分,并代入边界条件,可得 o)-ix-3x-jx 3
3 8.2 静电场中的矩量法 8.2.1 一维平行板电容器 0 1 x ( ) 2 0 两板间的电荷密度: = +1 4x (1)解析解 解:在区间x∈[0, 1]上,电位分布φ 满足泊松方程 ( ) 2 2 2 0 d 1 4 d x x = − = − + 其中,边界条件为φ(0) = φ(1) = 0 可对泊松方程进行两次积分,并代入边界条件,可得 ( ) 5 1 1 2 4 6 2 3 x x x x = − − 求解电容器两板间的电位分布

8.2静电场中的矩量法 956 (2)数值解 (MoM) 在区间x∈[0,1]上,电位分布0满足泊松方程 将用已知的全域基函数展开:p=之,0.=立a,(-x") 代入到泊松方程中,可得 Q1:为什么选择这样的基函数? 立a-r)-0+) Q2:方程是否可解?为什么? = 权函数采用点匹配法,在区间x∈[0,1]上选择N个离散点满足方程,即将该区间等 分为N+1个小区域,匹配点的位置为,xm=m/(N+1),m=1,2,,N,则 -x)=n+x.=n+》 1+4.=1+4 4
4 8.2 静电场中的矩量法 (2)数值解(MoM) 在区间x∈[0, 1]上,电位分布φ 满足泊松方程 将φ用已知的全域基函数展开: ( ) 1 1 1 N N n n n n n n a a x x + = = = = − 代入到泊松方程中,可得 Q1:为什么选择这样的基函数? ( ) ( ) 2 1 2 2 1 d 1 4 d N n n n a x x x x + = − = − + Q2:方程是否可解?为什么? 权函数采用点匹配法,在区间x∈[0, 1]上选择N个离散点满足方程,即将该区间等 分为N+1个小区域,匹配点的位置为, x m N m = + ( 1) ,m = 1, 2, …, N,则 ( ) ( ) ( ) 1 2 1 1 2 d 1 1 d 1 m n n n x x m x x n n x n n x N − + − = − = + = + + 2 2 1 4 1 4 m 1 x x m x = N + = + +

8.2静电场中的矩量法 当W=1时,解得a1=1。代入方程,得 0≈419=x-x2 当N=2时,有 ]. 解得a1=1/18,a2=2/3,代入方程得 *a9+a明- -1-2x 1818 3 22/3 3/4 5/4 当N=3时,有 23 3 42 2 。 解得a1=1/2,a2=0,a3=1/3,则 2 9/227/4a, 13/4 5 1 0≈419+a202+a03=5X1 数值解和解析解一致! 6
5 8.2 静电场中的矩量法 当N = 1时,解得 a1 = 1。代入方程,得 2 1 1 = − a x x 当N = 2时,有 。 1 2 2 2 13 9 2 4 25 9 a a = 解得a1 = 1/18, a2 = 2/3,代入方程得 2 3 1 1 2 2 13 1 2 18 18 3 + = − − a a x x x 1 2 3 2 2 3 3 4 5 4 2 3 3 2 2 9 2 27 4 13 4 a a a = 当N = 3时,有 。解得a1 = 1/2, a2 = 0, a3 = 1/3,则 2 4 1 1 2 2 3 3 5 1 1 6 2 3 + + = − − a a a x x x 数值解和解析解一致!
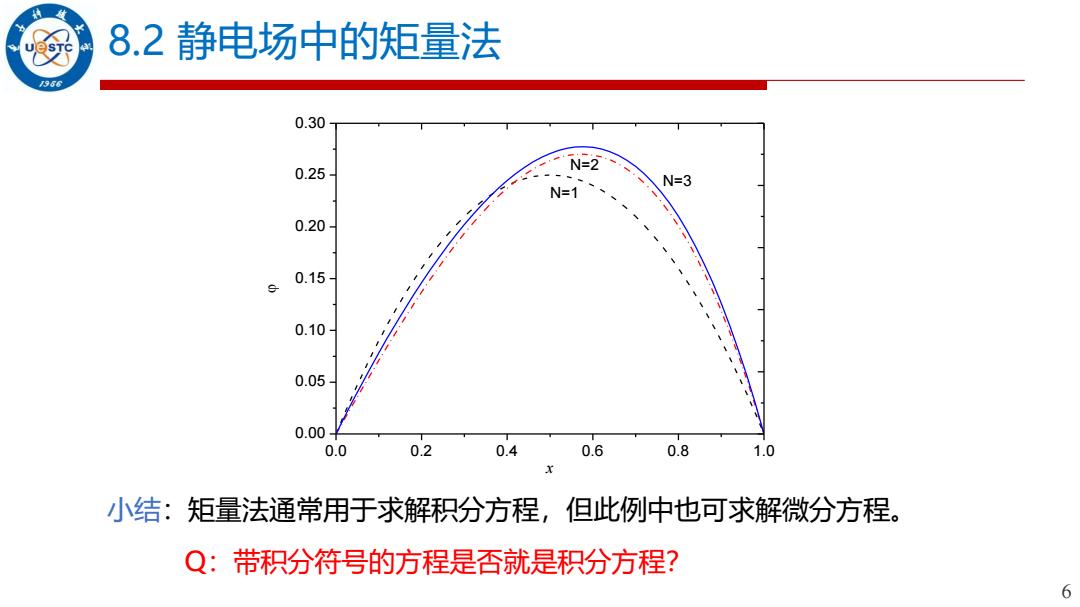
8.2静电场中的矩量法 966 0.30 N=2 0.25 N=3 N=1 0.20 0.15 0.10 0.05 0.00 0.0 0.2 0.4 0.6 0.8 1.0 小结:矩量法通常用于求解积分方程, 但此例中也可求解微分方程。 Q:带积分符号的方程是否就是积分方程? 6
6 8.2 静电场中的矩量法 0.0 0.2 0.4 0.6 0.8 1.0 0.00 0.05 0.10 0.15 0.20 0.25 0.30 N=3 N=2 N=1 x 小结:矩量法通常用于求解积分方程,但此例中也可求解微分方程。 Q:带积分符号的方程是否就是积分方程?