例 目录 第十一章矩量法应用 2
2 目 录 第十一章 矩量法应用
11.2二维金属目标的散射 11.2.1二维金属薄条带的散射 H 一个任意电磁场可以表示为一 个TM波和一个TE波之和 H TM(垂直极化) TE(平行极化) > 条带的EFIE(TM极化) 具有单位幅度的入射电场: E(p)= p H p =c'+snp) ysino E 均匀平面波 xcoSO Q:为什么指数项没有“-”号? 3
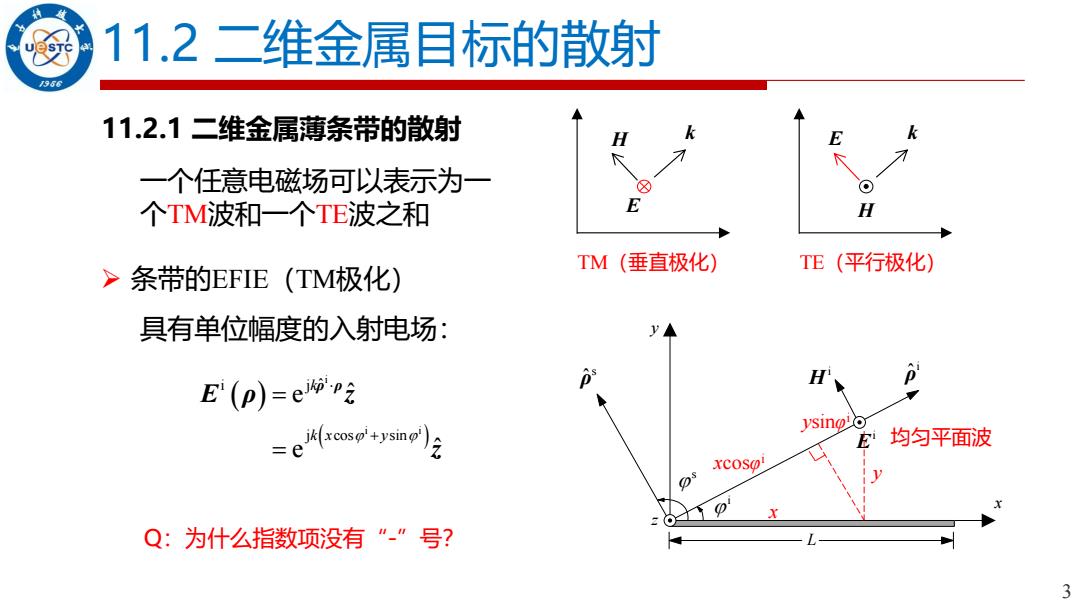
3 11.2 二维金属目标的散射 11.2.1 二维金属薄条带的散射 一个任意电磁场可以表示为一 个TM波和一个TE波之和 E H k TM(垂直极化) E H k TE(平行极化) ➢ 条带的EFIE(TM极化) z y x i E i H i ρ ˆ i s ρ ˆ s L 具有单位幅度的入射电场: ( ) ( ) i i i i j ˆ j cos sin e ˆ e ˆ k k x y + = = ρ ρ E ρ z z 均匀平面波 x y xcosφ i ysinφ i Q:为什么指数项没有“-”号?

11.2二维金属目标的散射 966 对应的入射磁场为:H(p)=-pxE 波阻抗n=√μ/e 7 sincc 1)入射电场E只有向分量,故表面感应电流密度也只有向分量; 2)条带非常薄,场量函数只沿x变化,由 aEo)=i(-f.ct.r)+vJ例小 (10-21) ou 得 国-jcpe)er 因为V,A A,A,OA. 0
4 11.2 二维金属目标的散射 对应的入射磁场为: ( ) ( ) ( ) i i i i i - j cos sin i i ˆ 1 sin cos e ˆ ˆ k x y + = − = − + E H ρ ρ x y 波阻抗 = 1)入射电场Ei只有z向分量,故表面感应电流密度J也只有z向分量; 2)条带非常薄,场量函数只沿x变化,由 ( ) ( ) ( ) ( ) ( ) ( ) i 2 j 1 ˆ ˆ , ' ' ' ' ' d ' S G k − = + n r E r n r r r J r J r r (10-21) 得 ( ) ( ) ( ) ( ) i 2 0 1 j , ' ' ' ' ' d ' ˆ L E x G J x J x x z z z k = + ρ ρ z =0 = x y z A A A x y z + + 因为 A

11.2二维金属目标的散射 1966 E:(x)=j@uJG(p.p).(x)dx y=0 由二维格林函数G(p,p)=-H(x-x0,得 年-1e-0 (9) y=0 用矩量法求解出了J后,散射场可以写为: E(p)=-婴J.(x)9(-x0d 大宗量近似 (r→∞) 0-omgG6ekor如 5
5 11.2 二维金属目标的散射 ( ) ( ) ( ) i 0 j , ' ' d ' L E x G J x x z z = ρ ρ ( ) ( ) ( ) 2 0 j , ' ' 4 由二维格林函数 G H k x x ρ ρ = − − ,得 ( ) ( ) ( ) i j cos 2 0 0 4 e ' ' d ' L kx z J x H k x x x = − (9) y = 0 y = 0 用矩量法求解出了Jz后,散射场可以写为: ( ) ( ) ( ) ( ) s 2 0 0 ' ' d ' 4 L E J x H k x x x z z = − − ρ 大宗量近似 (r→∞) ( ) ( ) s j s j 'cos 0 j e ' e d ' 8 k L kx E J x x z z k − = − ρ
11.2二维金属目标的散射 966 MoM求解 一脉冲基函数和点匹配法 金属条带在x方向分为N,每段△x=L/N,基函数采用脉冲基函数、权函数采 用点匹配法,由式(9)得 源点x和匹配点xm都位于各分段的中点 4 b= 1)当x,和x,m不重合时,近似处理积分 三m=Hg2(kxm-x)Ax 6
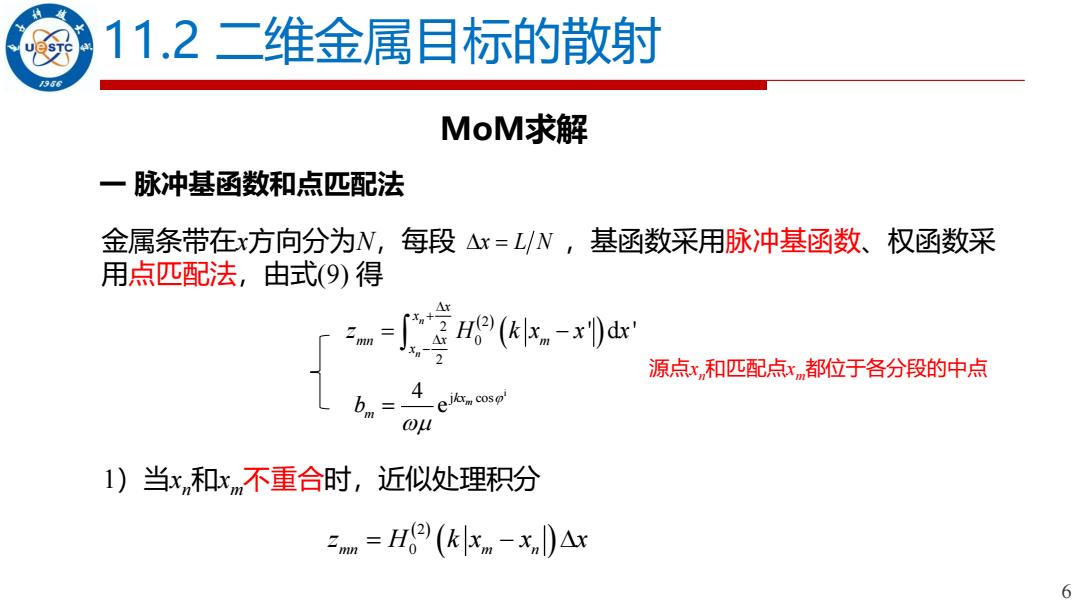
6 11.2 二维金属目标的散射 一 脉冲基函数和点匹配法 MoM求解 金属条带在x方向分为N,每段 ,基函数采用脉冲基函数、权函数采 用点匹配法,由式(9) 得 = x L N ( ) ( ) 2 2 0 2 ' d ' n n x x mn m x x z H k x x x + − = − 源点xn和匹配点xm都位于各分段的中点 i 4 j cos e kxm m b = 1)当xn和xm不重合时,近似处理积分 ( ) ( ) 2 mn m n 0 z H k x x x = −