
计算电磁学 (小班研讨课) 966 录 第十章积分方程 目 2
2 计算电磁学(小班研讨课) 目 录 第十章 积分方程

10.4细导线的线积分方程 966 场点 10.4.1细线近似 源点 a a<<L→细线→开放结构→EFIE J(r)=- : J与方位角p无关, 2 2πa 并在两端为零 圆柱坐标系下,磁矢量位A可由表面积分得到 d dl'=ado' IP-P' aor do' 余弦定理 r=Ir-r1=y--z)+l-pT lp-pf=pita-2p-p 该式是(0'-p)的函数,结果轴对称 =p2+a2-2pac0s(p'-p)) 用p'替代(p'-p) 3
3 2a z 2 L 2 L − o r ' r z z − ' ρ − ρ ' 10.4.1 细线近似 10.4 细导线的线积分方程 a << L → 细线 → 开放结构 → EFIE ( ) ( ) ˆ 2 z I z a J r z = J与方位角φ无关, 并在两端为零 圆柱坐标系下,磁矢量位Az可由表面积分得到 ( ) ( ) j 2 2 0 2 ' e , , d 'd ' 2 4 L kr z z L I z A z z r − − = d𝜑’ 𝑎 dl’ d '= d ' l a ( ) 2 2 r z z = − = − + − r r' ' ' ρ ρ ρ − ρ ' ρ ' ρ '− 余弦定理 ( ) 2 2 2 2 2 ' 2 ' 2 cos ' a a a − = + − = + − − ρ ρ ρ ρ a 该式是( '− ) 的函数,结果轴对称 用 ' 替代 ( '− ) 源点 场点
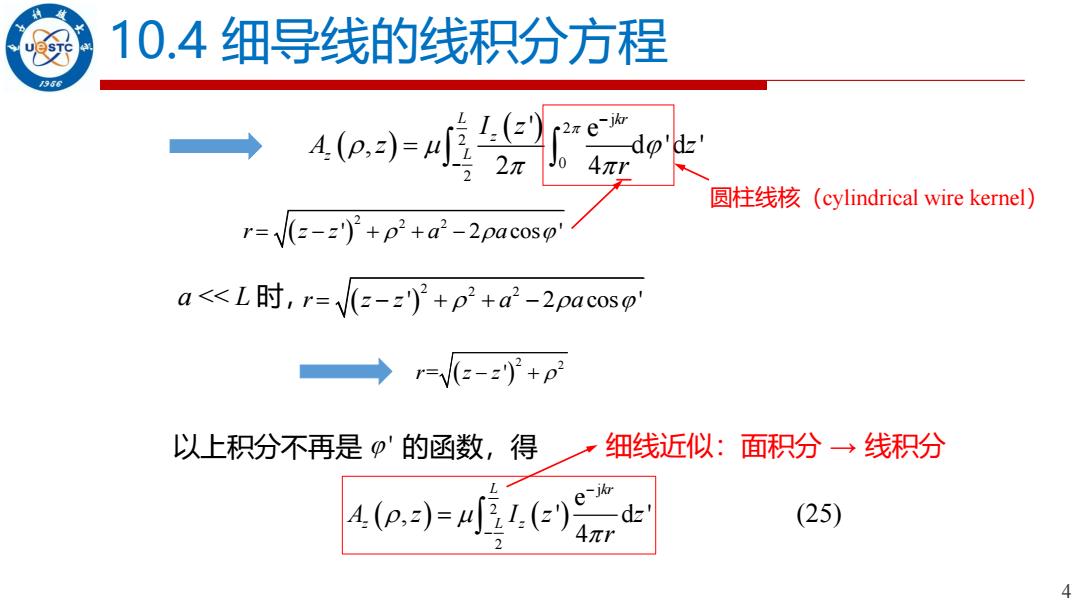
10.4细导线的线积分方程 966 A(p,)= 人空x三 do'dz' 2元 4πr 圆柱线核(cylindrical wire kernel) r=/(=-:)'+p+a-2pacoso" a<L时,r=V(z-z2+p2+a2-2 pacos ◆ r=v(E-=)+e 以上积分不再是'的函数,得 细线近似:面积分→线积分 4(D)=1,(e (25) 4
4 10.4 细导线的线积分方程 ( ) ( ) j 2 2 0 2 ' e , d 'd ' 2 4 L kr z z L I z A z z r − − = ( ) 2 2 2 r z z a a = − + + − ' 2 cos ' 圆柱线核(cylindrical wire kernel) a << L 时, ( ) 2 2 2 r z z a a = − + + − ' 2 cos ' ( ) 2 2 r z z = ' − + 以上积分不再是 ' 的函数,得 ( ) ( ) j 2 2 e , ' d ' 4 L kr A z I z z z z L r − − = (25) 细线近似:面积分 → 线积分

10.4细导线的线积分方程 9656 由式(15)E=-j0A-」V(·A)的标量场形式: @LE E=-joA-jo (26) 未知 未知 未知 通过线表面的切向场边界条件,得到关于入射场E的细线EFIE Ei=- (27) 思考:从(26)推导出(27 ⊙IE 其中,r=-z)2+a。 电流只在线的表面流动,但由于导线很细,表 面电流可等效为位于轴上线电流的作用 注意:这里由p变成了a 5
5 10.4 细导线的线积分方程 通过线表面的切向场边界条件,得到关于入射场 Ei 的细线EFIE 2 i 2 2 j E k A z z z = + (27) ( ) 2 2 其中, r z z a = − + ' 。 电流只在线的表面流动,但由于导线很细,表 面电流可等效为位于z轴上线电流的作用 思考:从(26)推导出(27) 注意:这里由 ρ 变成了a ( ) j j 由式(15) E A A = − − 的标量场形式: 2 s 2 j j E A A z z z z = − − 未知 未知 未知 (26)
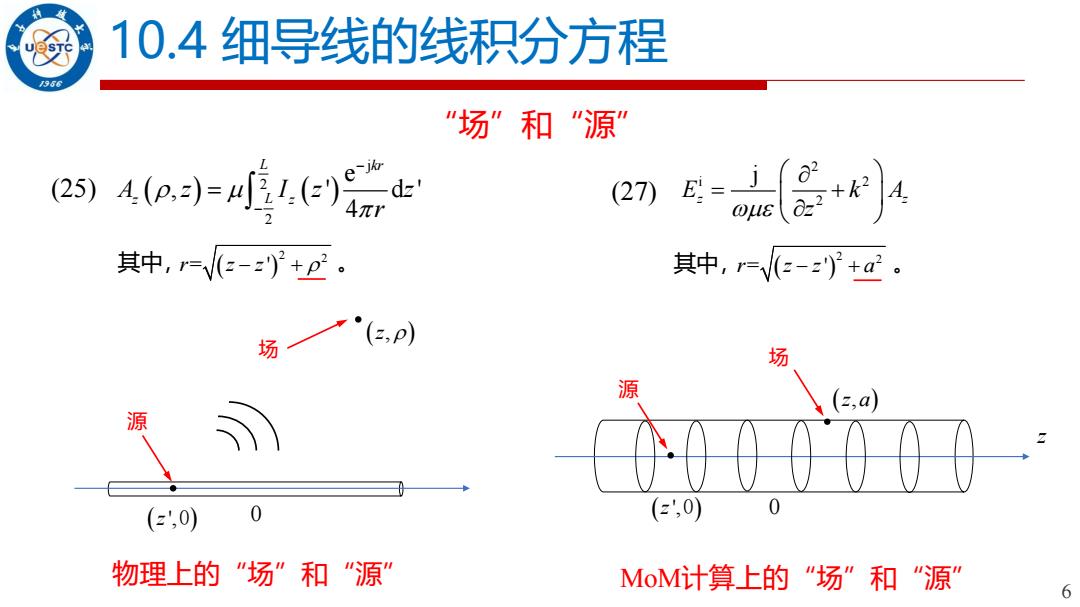
10.4细导线的线积分方程 966 “场”和“源 25)Ao=j值L(e)rd止 (27) E:=-J6 其中,=-+p2。 其中,=e-+a2。 场 (a,p) 场 源 (z,a 源 (',0) 0 (z',0) 物理上的“场”和“源” MoM计算上的"场”和“源" 6
6 10.4 细导线的线积分方程 “场”和“源” ( ) ( ) j 2 2 e , ' d ' 4 L kr A z I z z z z L r − − = (25) ( ) 2 2 其中, r z z = ' − + 。 (27) 2 i 2 2 j E k A z z z = + ( ) 2 2 其中, r z z a = ' − + 。 0 z (z',0) 源 (z, ) 场 物理上的“场”和“源” MoM计算上的“场”和“源” 源 (z',0) 场 0 (z a, )