一 arctan x 例2.求1im 型 0 x>+00 X 解:原式=lm 1+x X>+00 co 型 o∞ lim x→+01+x X→+00 HIGH EDUCATION PRESS ©色OC①8 机动目录上页下页返回结束
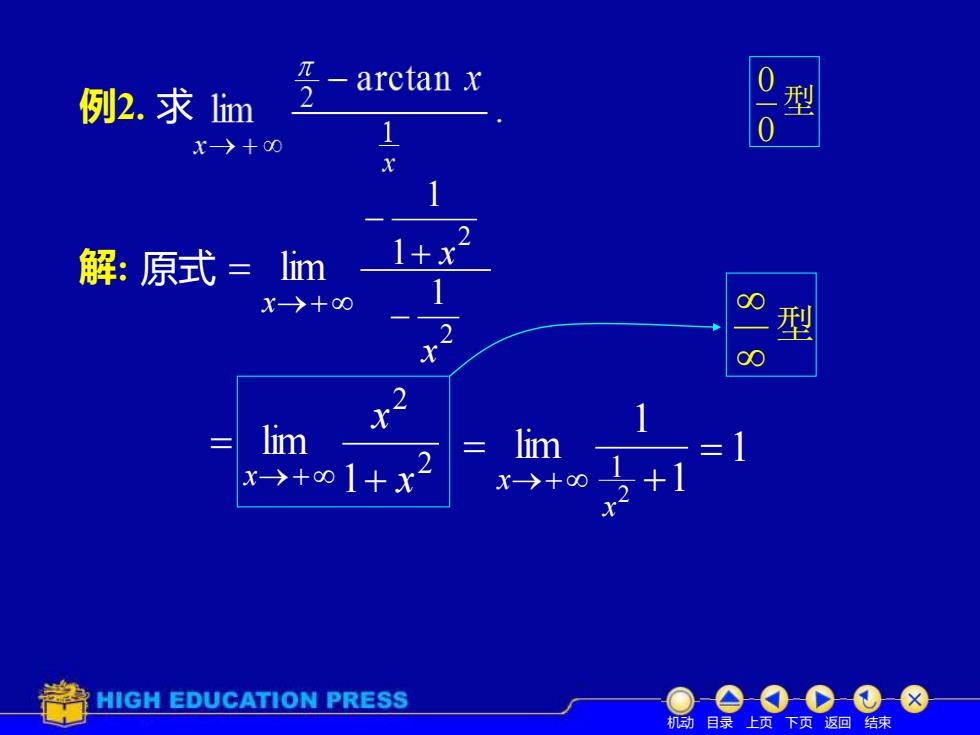
例2. 求 解: 原式 lim →+ = x 型 0 0 2 2 1 lim x x x + = →+ = 1 2 1 1 + x − 2 1 x − 1 1 lim 2 1 + = →+ x x 型 机动 目录 上页 下页 返回 结束

二、型未定式 00 定理2. 1)lim f(x)=lim F(x)=c0 x→d x→d 2)f(x)与F(x)在U(a)内可导,且F'(x)≠0 3)1im 存在(或为∞) x->a F(x) lim f() =limx) (洛必达法则 x->a F(x) xaF(x) HIGH EDUCATION PRESS 机动目录上页下页返回结束
二、 型未定式 ( ) ( ) 3) lim F x f x x a → 存在 (或为∞) ( ) ( ) lim F x f x x→a 定理 2. ( ) ( ) lim F x f x x a = → (洛必达法则) 机动 目录 上页 下页 返回 结束 2) f (x)与F(x) 在 (a)内可导,

说明:定理中x→a换为 x→a, x->a, X→0, X→+0, X一00 之一,条件2)作相应的修改,定理仍然成立 HIGH EDUCATION PRESS @色OC①8 定理2目录上页下页返回结束
说明: 定理中 x → a 换为 之一, 条件 2) 作相应的修改 , 定理仍然成立. , → + x a , → − x a x → , x → +, x → − 定理2 目录 上页 下页 返回 结束