说明: (1)机构有极位夹角,就有急回性: (2)0越大,K值越大,急回性就越显著: (3)0=180K-。(设计时一般都先给出K) K+1 急回特性的作用:可以缩短非生产时间,提高生产率。 A。偏置曲柄滑块机构的极位夹角见下图1。 A 图1 H 行程速比系数K同曲柄摇杆机构。 8=Ψ 注:对心式曲柄滑块机构无急回性。 图2 B.导杆机构的极位夹角见上图2。 行程速比系数K同曲柄摇杆机构。 4.5.4死点 1.死点的位置: 在曲柄摇杆机构中(上面图0) 若以摇杆为原动件,当连杆与从动件(曲柄)共线时的位置称死点位置。这时机构的 传动角Y=0,压力角a=90,即连杆对从动曲柄的作用力恰好通过其回转中心A,不能推 动曲柄转动。 存在死点位置的标志是:连赶与从动件共线。 摇杆为原动件,有2个死点位置: 曲柄为原动件,没有死点位置。(因连杆与从动杆不会共线 B.在导杆机构中(上面图2) 曲柄为原动件时,没有死点位置:反之,则有2个。 C. 在曲柄滑块机构中(上面图1) 曲柄为原动件时,没有死点位置:反之,则有2个。 2.出现死点的利弊: 利:工程上利用死点进行工作。 如:飞机起落架(图4.40)、夹紧机构(图4.41 弊:机构有死点,从动件将出现卡死或运动方向不确定现象,对机构传动不利。 3.渡过死点位置的方法: (1)在从动件上安装飞轮,借飞轮惯性,使机构顺利通过死点。如:缝纫机。 (2)采用机构错位排列的方法。 如:机车车轮联动机构
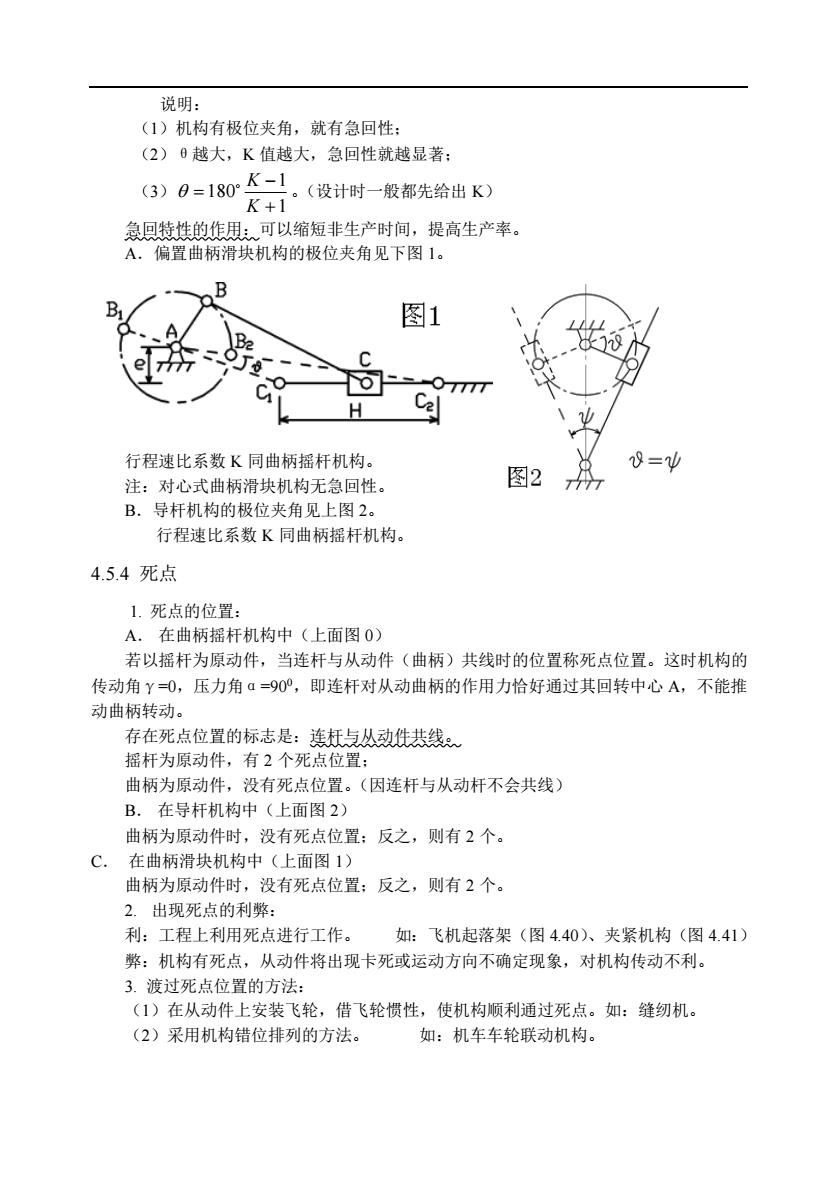
说明: (1)机构有极位夹角,就有急回性; (2)θ越大,K 值越大,急回性就越显著; (3) 1 1 180 + − = K K 。(设计时一般都先给出 K) 急回特性的作用:可以缩短非生产时间,提高生产率。 A.偏置曲柄滑块机构的极位夹角见下图 1。 行程速比系数 K 同曲柄摇杆机构。 注:对心式曲柄滑块机构无急回性。 B.导杆机构的极位夹角见上图 2。 行程速比系数 K 同曲柄摇杆机构。 4.5.4 死点 1. 死点的位置: A. 在曲柄摇杆机构中(上面图 0) 若以摇杆为原动件,当连杆与从动件(曲柄)共线时的位置称死点位置。这时机构的 传动角γ=0,压力角α=900,即连杆对从动曲柄的作用力恰好通过其回转中心 A,不能推 动曲柄转动。 存在死点位置的标志是:连杆与从动件共线。 摇杆为原动件,有 2 个死点位置; 曲柄为原动件,没有死点位置。(因连杆与从动杆不会共线) B. 在导杆机构中(上面图 2) 曲柄为原动件时,没有死点位置;反之,则有 2 个。 C. 在曲柄滑块机构中(上面图 1) 曲柄为原动件时,没有死点位置;反之,则有 2 个。 2. 出现死点的利弊: 利:工程上利用死点进行工作。 如:飞机起落架(图 4.40)、夹紧机构(图 4.41) 弊:机构有死点,从动件将出现卡死或运动方向不确定现象,对机构传动不利。 3. 渡过死点位置的方法: (1)在从动件上安装飞轮,借飞轮惯性,使机构顺利通过死点。如:缝纫机。 (2)采用机构错位排列的方法。 如:机车车轮联动机构

4.6平面四杆机构的设计 一个设计过程:由己知条件一设计出各构件尺寸 √已知条件: 运动条件(如:从动件的运动规律) 几何条件(如:杆的尺寸范围) 动力条件(如:满足Ymin>400) 两类基本问题 √实现给定运动规律:(位置、速度、加速度、行程速比系数K) √实现给定运动轨迹。 三种设计方法: √图解法利用几何作图原理求解:图解法比较简明易懂,求解快,手工绘图精度 稍差:但计算机绘图已完全解决这一问题,其精度远远满足工程需要。 解析法:利用和构建设计参数间的函数关系求解:可以使设计呈参数化,精度高 但比较繁杂,如今利用计算机(CAD)也使得解析法变得轻松和容易。 √实验法:利用试凑法和连杆曲线图谱等方法求解:实验法直观、迅速,可近似达 到要求,常用作设计的预选。 4.6.1图解法设计平面四杆机构 图解法设计步骤: (1)将己知的几何条件能画出的尽可能画出: (2)将给定的运动条件转化为几何条件:(这一步往往要应用一些平面几何知识) (3)根据其他辅助条件求出所需机构。 注意:对动力学条件(如Ym),若给定的辅助条件中没有,或设计作图过程中也没 有涉及到,则求得的机构,还要校核Ym是否在允许值范围内。 1.按给定连杆位置设计四杆机构 已知:连杆BC长度及三个位置(B1C、B2C2、BC)。 要求:设计铰链四杆机构。(图4.42) 设计步骤: (I)连接B1B2、BB,作线BB2、B2B的垂直平分线b12、b23,交于A点: (2)连接C1C2、CC,作线CC2、CC3的垂直平分线c12、c23,交于D点: (3)连接AB1、CD,即得所求。 2.按给定两连架杆的对应位置设计四杆机构 解决此类问题常用刚化反转法。 所谓刚化反转法即将四杆机构在某一位置刚化后反 转一个角度。刚化反转的演示如下: 若己知机架AD、连架杆AB的长度及连架杆AB、CD的两组对应位置a1、中1和a2 中2,试设计该铰链四杆机构。(图4.43》 此问颗的关键是求较链C的位置 将AB2C2D刚化后绕D点反转(中~中2)角,CD与CD重合,AB2转到A'B2'的位 置。注意:经过转换,A、A'点相当于绕D点转动,B1、B2'点相当于绕C1点转动。这
4.6 平面四杆机构的设计 一个设计过程:由已知条件→设计出各构件尺寸 ✓ 已知条件: 运动条件(如:从动件的运动规律) 几何条件(如:杆的尺寸范围) 动力条件(如:满足γmin>400) 两类基本问题: ✓ 实现给定运动规律;(位置、速度、加速度、行程速比系数 K) ✓ 实现给定运动轨迹。 三种设计方法: ✓ 图解法;利用几何作图原理求解;图解法比较简明易懂,求解快,手工绘图精度 稍差;但计算机绘图已完全解决这一问题,其精度远远满足工程需要。 ✓ 解析法;利用和构建设计参数间的函数关系求解;可以使设计呈参数化,精度高, 但比较繁杂,如今利用计算机(CAD)也使得解析法变得轻松和容易。 ✓ 实验法:利用试凑法和连杆曲线图谱等方法求解;实验法直观、迅速,可近似达 到要求,常用作设计的预选。 4.6.1 图解法设计平面四杆机构 图解法设计步骤: (1)将已知的几何条件能画出的尽可能画出; (2)将给定的运动条件转化为几何条件;(这一步往往要应用一些平面几何知识) (3)根据其他辅助条件求出所需机构。 注意:对动力学条件(如γmin),若给定的辅助条件中没有,或设计作图过程中也没 有涉及到,则求得的机构,还要校核γmin 是否在允许值范围内。 1. 按给定连杆位置设计四杆机构 已知:连杆 BC 长度及三个位置(B1C1、B2C2、B3C3)。 要求:设计铰链四杆机构。(图 4.42) 设计步骤: (1) 连接 B1B2、B2B3,作线 B1B2、B2B3 的垂直平分线 b12、b23,交于 A 点; (2) 连接 C1C2、C2C3,作线 C1C2、C2C3 的垂直平分线 c12、c23,交于 D 点; (3) 连接 AB1、C1D,即得所求。 2. 按给定两连架杆的对应位置设计四杆机构 解决此类问题常用刚化反转法。 所谓刚化反转法即将四杆机构在某一位置刚化后反 转一个角度。刚化反转的演示如下: 若已知机架 AD、连架杆 AB 的长度及连架杆 AB、CD 的两组对应位置α1、φ1 和α2、 φ2,试设计该铰链四杆机构。(图 4.43) 此问题的关键是求铰链 C 的位置。 将 AB2C2D 刚化后绕 D 点反转(φ1-φ2)角,C2D 与 C1D 重合,AB2 转到 A′B2′的位 置。注意:经过转换,A、A′点相当于绕 D 点转动,B1、B2′点相当于绕 C1 点转动。这

样原问题可转化为按连杆的两位置设计四杆机构。 3.按给定行程速比系数K设计四杆机构 A.按给定行程速比系数K设计曲柄摇杆机构 设已知摇杆CD的长度c、摆角中和行程速比系数K,试设计该曲柄摇杆机构。 该设计的关键是确定固定铰链A的位置。设计步骤如下:(图4.45) (1)选取适当比例尺μL,按c和中作出摇杆的两个极限位置CD和CD: (2)按式0=180K=算出极位夹角: K+1 (3)连接C1C2,作∠CC20=∠C2C10=90°-0,以0为圆心、0C为半径作圆n, ∠C10C2=20: (4) 在圆n上,弧CC2所对圆周角上取A点,∠C1OC2=,则AC、AC,即为曲柄与 连杆共线的两个位置。设曲柄与连杆的长度分别为a和b, 则 u,·AC=b-a,μ:·AC=b+a 于是曲柄长度a=μ:(AC2-AC)/2 连杆长度b=μL(AC2+AC)/2 B.按给定行程速比系数K设计导杆机构 已知摆动导杆机构的机架长度d和行程速比系数K,试设计该机构。(图4.46) 解:取比例尺μ,作AD=d/μ1。由K算出8,由图可知,极位夹角等于导杆的摆 角中,因此作∠ADB1=∠ADB2=O/2,作AB,或AB垂直于B,D(或BD),则AB就是曲 柄,其长度a=uL·AB。 4.6.2解析法设计平面四杆机构 用解析法设计平面四杆机构时,首先要建立方程式,然后根据已知参数对方程式 求解。下面介绍解决按给定两连架杆对应位置设计四杆机构的问题。 已知:连架杆AB和CD的三对对应位置p1V1、922、p,要求确定各构件的长度 a、b、c、d。(图4.47) 分析:此机构各杆长度按同一比例增减时,各杆转角间的关系不变,故只需确定各杆 的相对长度,取a=l,则待求参数只有三个。 由于该机构四杆组成封闭多边形,因而有矢量方程式: a+b=d+c(二边矢量和等于第三边矢量) 为便于用解析法,可取直角坐标系XAY(以机架AD为X轴),取各杆在X、Y轴的 投影分别代入上式可得: cosp+bcos6=d ccosw sin+bsin=csinw 消去8,整理,并令:R=c、R=-(c/d)、R=(d+c2+1-b2V2d 得: cos中=R1cos+Rcog-中)+R3
样原问题可转化为按连杆的两位置设计四杆机构。 3. 按给定行程速比系数 K 设计四杆机构 A. 按给定行程速比系数 K 设计曲柄摇杆机构 设已知摇杆 CD 的长度 c、摆角 ψ 和行程速比系数 K,试设计该曲柄摇杆机构。 该设计的关键是确定固定铰链 A 的位置。设计步骤如下:(图 4.45) (1) 选取适当比例尺μL,按 c 和 ψ 作出摇杆的两个极限位置 C1D 和 C2D; (2) 按式 1 1 180 + − = K K 算出极位夹角θ; (3) 连接 C1C2,作∠C1C2O=∠C2C1O=90°-θ,以 O 为圆心、OC1 为半径作圆η, ∠C1 O C2=2θ; (4) 在圆η上,弧 C1C2 所对圆周角上取 A 点,∠C1 O C2=,则 AC1、AC2 即为曲柄与 连杆共线的两个位置。设曲柄与连杆的长度分别为 a 和 b, 则 μL·AC1=b-a , μL·AC2= b+a 于是 曲柄长度 a=μL(AC2 - AC1)/2 连杆长度 b=μL(AC2 + AC1)/2 B.按给定行程速比系数 K 设计导杆机构 已知摆动导杆机构的机架长度 d 和行程速比系数 K,试设计该机构。(图 4.46) 解:取比例尺μL,作 AD=d/μL。由 K 算出θ,由图可知,极位夹角θ等于导杆的摆 角 ψ,因此作∠ADB1=∠ADB2=θ/2,作 AB1 或 AB2 垂直于 B1D(或 B2D),则 AB 就是曲 柄,其长度 a=μL·AB1。 4.6.2 解析法设计平面四杆机构 用解析法设计平面四杆机构时,首先要建立方程式,然后根据已知参数对方程式 求解。下面介绍解决按给定两连架杆对应位置设计四杆机构的问题。 已知:连架杆 AB 和 CD 的三对对应位置 φ1ψ1、φ2ψ2、φ3ψ3,要求确定各构件的长度 a、b、c、d。 (图 4.47) 分析:此机构各杆长度按同一比例增减时,各杆转角间的关系不变,故只需确定各杆 的相对长度,取 a=1,则待求参数只有三个。 由于该机构四杆组成封闭多边形,因而有矢量方程式: a + b = d + c (二边矢量和等于第三边矢量) 为便于用解析法,可取直角坐标系 XAY(以机架 AD 为 X 轴),取各杆在 X、Y 轴的 投影分别代入上式可得: cosφ + bcosδ = d + ccosψ sinφ + bsinδ = csinψ 消去 δ,整理,并令:R1=c、R2=-(c/d)、R3=(d2+c2+1-b 2 )/2d 得: cosφ = R1cosψ + R2cos(ψ-φ) + R3

上式即为两连架杆转角之间的关系式,将已知的三对对应转角p1y 、33分别 代入,可得方程组。解方程组求出R、R2、R,再将他们代入相应式子,即可求得b、c d(注:它们是相对于a的相对长度)。 若根据具体情况选定曲柄长度a后,则b、c、d均可确定
上式即为两连架杆转角之间的关系式,将已知的三对对应转角 φ1ψ1、φ2ψ2、φ3ψ3 分别 代入,可得方程组。解方程组求出 R1、R2、R3,再将他们代入相应式子,即可求得 b、c、 d(注:它们是相对于 a 的相对长度)。 若根据具体情况选定曲柄长度 a 后,则 b、c、d 均可确定
福建交通职业技术学院教案纸 第27项 课程: 学年第_学期第周一月一日 教学内容 备注 例题: 1.四杆机构的杆长计算例题 在图示机构中,已知:LBc=50mm、Lcp=35mm、LaD=30mm,AD为机架。试求: (1)若此机构为曲柄摇杆机构,且AB为曲柄,求LAB的最大值? (2)若此机构为双曲柄机构,求LB的最小值? (3)若此机构为双摇杆机构,求LAB的数值? 2.图解法求曲柄摇杆机构的K、Ymn 图示曲柄摇杆机构,AB=15cm,BC-30cm,CD=25cm,AD=35cm,试用图解法求K、Ymin。 B ● 0 例题1图 例题2图 3.图解法设计曲柄摇杆机构 设计一如图所示脚踏轧棉机的曲柄摇杆机构 要求:踏板CD在水平位置上下各摆10°, CD=500mm,AD=1000mm, 试用几何作图法求曲柄AB和连杆BC的长度。 4.图解法设计机床变速箱操纵机构
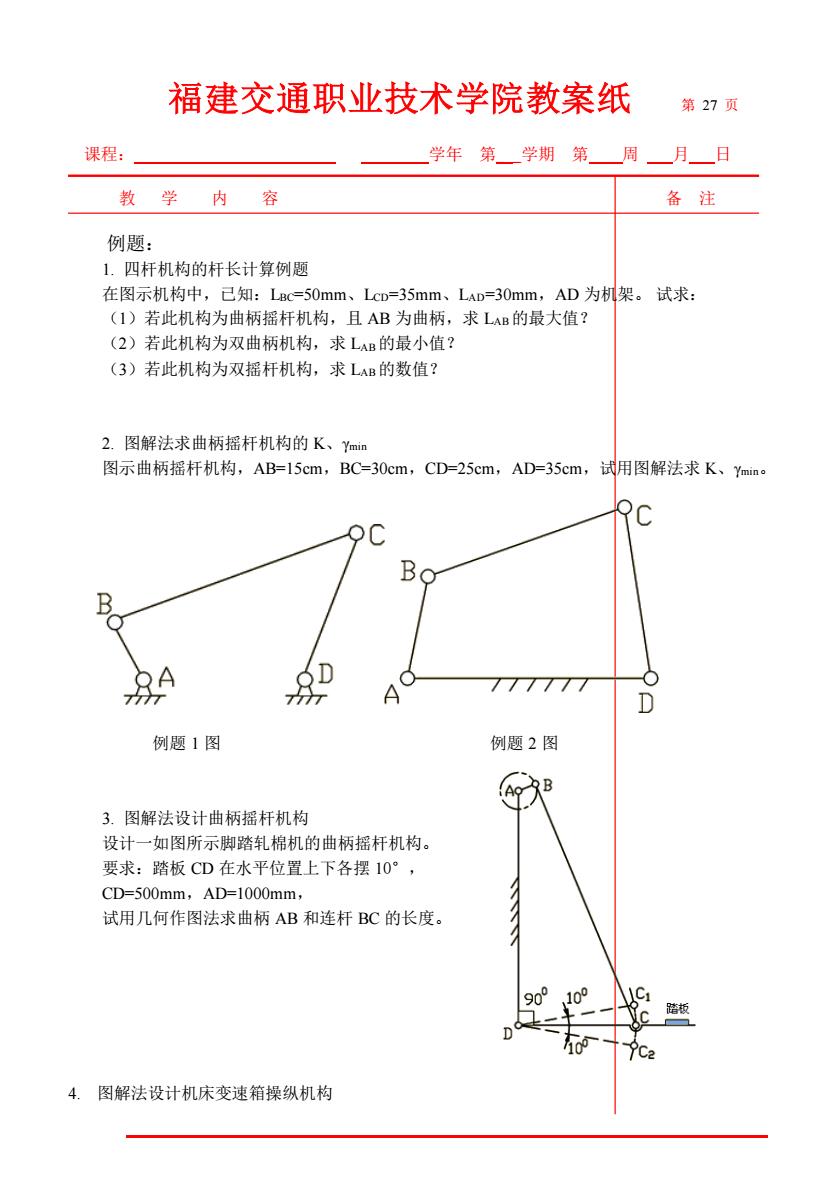
福建交通职业技术学院教案纸 第 27 页 课程: 学年 第_ _学期 第 周 月 日 教 学 内 容 备 注 例题: 1. 四杆机构的杆长计算例题 在图示机构中,已知:LBC=50mm、LCD=35mm、LAD=30mm,AD 为机架。 试求: (1)若此机构为曲柄摇杆机构,且 AB 为曲柄,求 LAB的最大值? (2)若此机构为双曲柄机构,求 LAB的最小值? (3)若此机构为双摇杆机构,求 LAB的数值? 2. 图解法求曲柄摇杆机构的 K、γmin 图示曲柄摇杆机构,AB=15cm,BC=30cm,CD=25cm,AD=35cm,试用图解法求 K、γmin。 例题 1 图 例题 2 图 3. 图解法设计曲柄摇杆机构 设计一如图所示脚踏轧棉机的曲柄摇杆机构。 要求:踏板 CD 在水平位置上下各摆 10°, CD=500mm,AD=1000mm, 试用几何作图法求曲柄 AB 和连杆 BC 的长度。 4. 图解法设计机床变速箱操纵机构