
2.7等效电源定理 三、戴维南等效内阻的计算★ 总结 1.外加电源法:将内部激励源全部置零,可简化内 部电路,利于分析; 2.开路短路法:一次性解决激励源取值和等效内阻 取值 3.伏安关系法:适合工程实践!原因:不易烧毁电 源,也避免了外加电源的内阻问题。 4.上述三种方法,也能用于纯电阻情形!
6 2.7 等效电源定理 三、戴维南等效内阻的计算★ 总结 1. 外加电源法:将内部激励源全部置零,可简化内 部电路,利于分析; 2. 开路短路法:一次性解决激励源取值和等效内阻 取值 3. 伏安关系法:适合工程实践!原因:不易烧毁电 源,也避免了外加电源的内阻问题。 4. 上述三种方法,也能用于纯电阻情形!
2.7等效电源定理 四、应用举例 例:如图(a)所示电路,已知当R=92时I=0.4A,若R变为72 时,其上的电流又为多大?(Us,s未知!oC,isc无法求!) 解:(1)求R。 将图(a)中电压源短路,电流源开路得 到No,并外加电流源I,如图(b)所示。 由KCL得I=3L1-I,则1=0.5I 由KVL和OL列A回路方程为 D U=2I-2I1=2I-2×0.5I=I 所以R=UI=12 (a 22 22 (2)画出戴维南等效电路,并接上 R,得图(c)电路。由该电路得 Uoc_ Uoc Ro+RL 1+RL (b) 代入已知条件,么==04 1+9 ,解得Uoc=4V 3)将R=72代入上式,得出相应的电流1=4/1+7)=0.5A
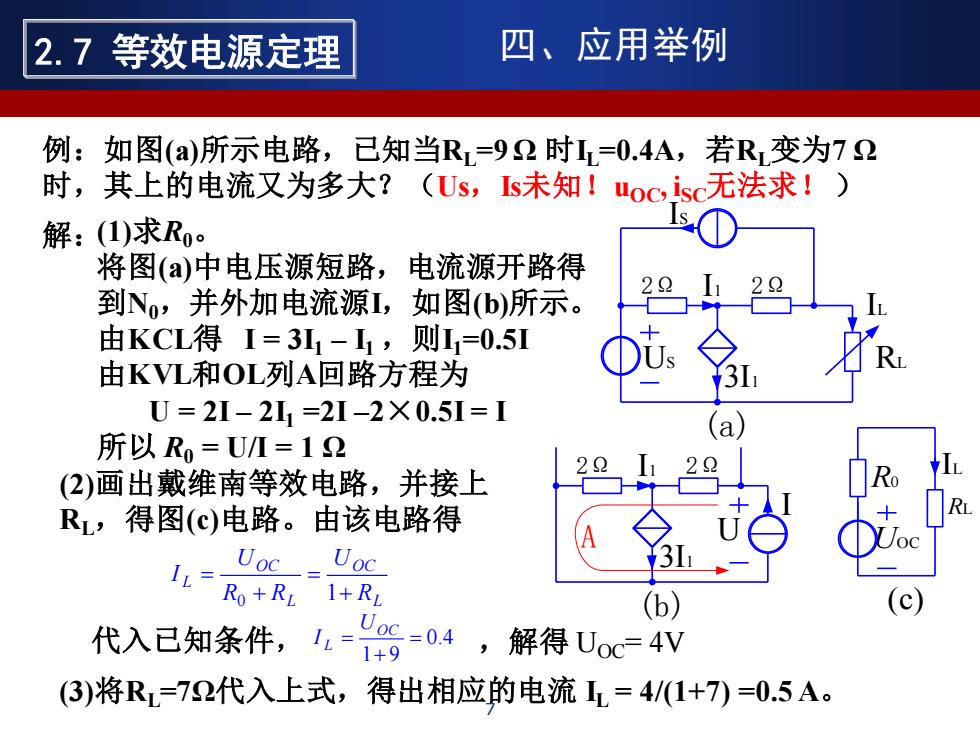
例:如图(a)所示电路,已知当RL=9 Ω 时IL=0.4A,若RL变为7 Ω 时,其上的电流又为多大?(Us,Is未知!uOC, iSC无法求! ) 解:(1)求R0。 将图(a)中电压源短路,电流源开路得 到N0,并外加电流源I,如图(b)所示。 由KCL得 I = 3I1 – I1 ,则I1=0.5I 由KVL和OL列A回路方程为 U = 2I – 2I1 =2I –2×0.5I = I 所以 R0 = U/I = 1 Ω (2)画出戴维南等效电路,并接上 RL,得图(c)电路。由该电路得 L OC L OC L R U R R U I + = + = 1 0 (3)将RL=7Ω代入上式,得出相应的电流 IL = 4/(1+7) =0.5 A。 代入已知条件, 0.4 1 9 = + = OC L U I ,解得 UOC= 4V 2Ω I1 2Ω IS US 3I1 IL RL (a) 2Ω I1 2Ω 3I1 I (b) A U RL IL UOC R0 (c) 7 2.7 等效电源定理 四、应用举例