
生物大分子波谱学原理 吴季辉 7.4三共振谱 -C-H H H-C一H H-C-H HNCA HCACO C-H HN(CO)CA HCA(CO)N HNCO CBCANH H HN(CA)CO CBCA(CO)NH H(CA)NH HBHA(CBCACO)NH ①©一@ H-C-H HBHA(CBCA)NH C(CO)NH-TOCSY
7.4 三共振谱 生物大分子波谱学原理 吴季辉
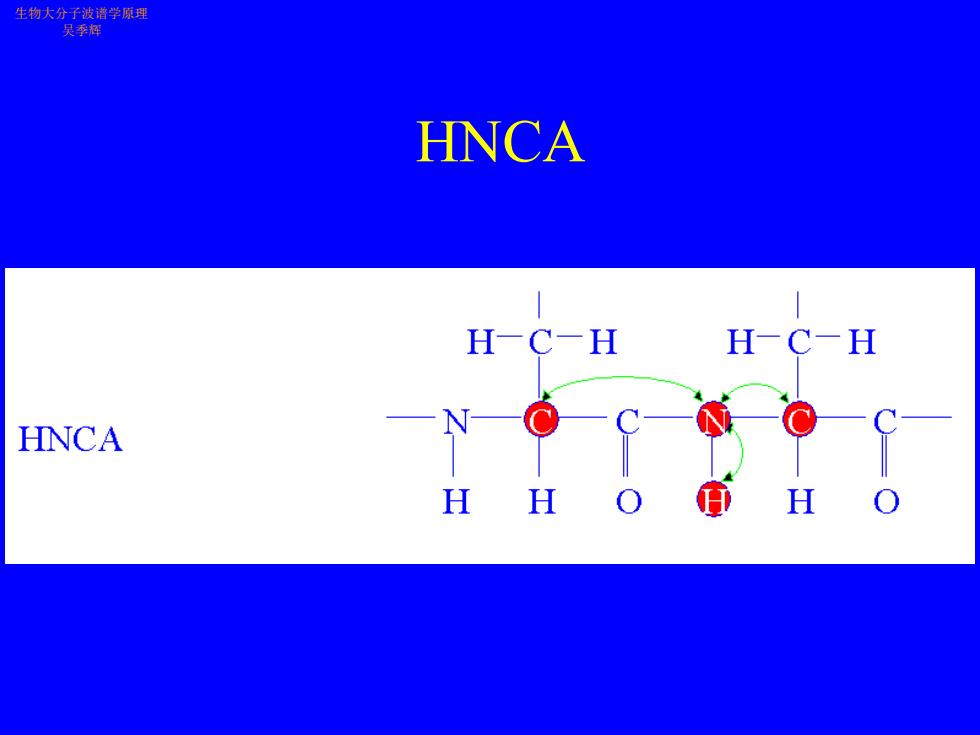
生物大分子波谱学原理 吴季辉 HNCA H-C-H H-C-H HNCA H H H
HNCA 生物大分子波谱学原理 吴季辉
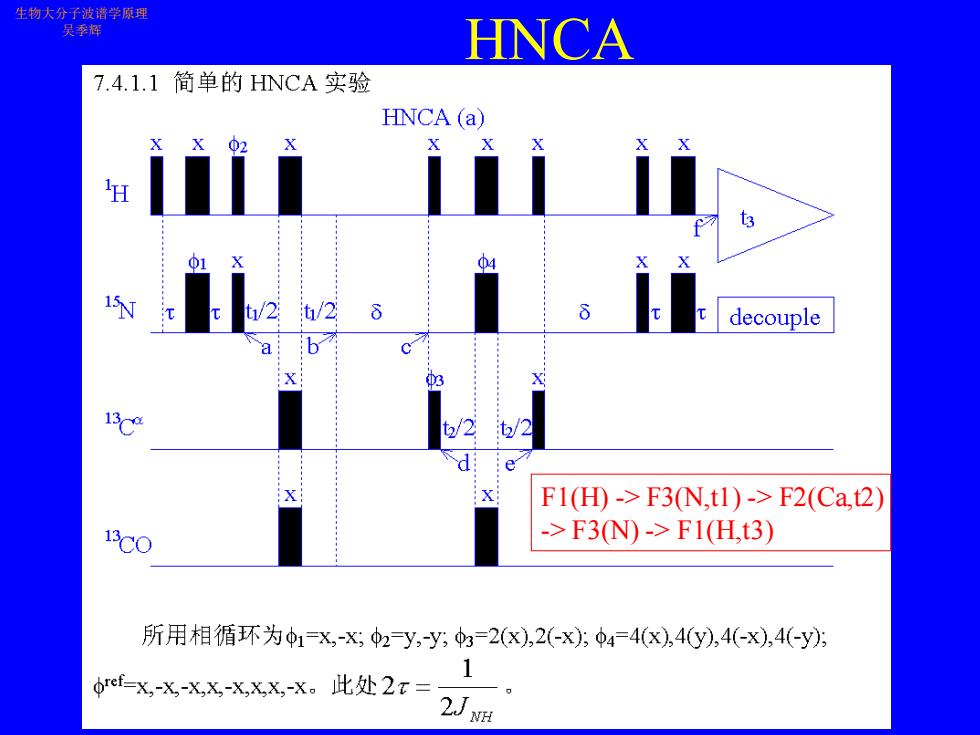
生物大分子波谱学原理 吴季辉 HNCA 7.4.1.1简单的HNCA实验 HNCA(a) X02 X X 01 ①4 /2 decouple 13C F1(D->F3N,t1)->F2(Ca,t2) 13C0 ->F3N)->F1(H,t3) 所用相循环为1=X,-x;中2y,-y,3=2(x),2(-x):4=4(x),4y),4(-x),4(-y) ref=x,-x-XX-x,xx,-X。此处2x= QJNH
HNCA 生物大分子波谱学原理 吴季辉 F1(H) -> F3(N,t1) -> F2(Ca,t2) -> F3(N) -> F1(H,t3)

生物大分子波谐学原理 7.4.11简单的HNCA实验 吴季辉 HNCA HNCA (a) decouple co 从HN的信号出发,经过第一个INEPT,传递给5N:O。=-2HN 经1期间频率标记:o6=-2HN,cos(Q4) 所用相循环为-xxy少的-2,2x◆44(x,4y4x,4(y) 1 =X-X-XXX,XX-X。此处2x= 在随后的8期间,产生N相对C“的反相磁化: 2J ge=4HN.CT,(⑥)+4HN.C-a「2(8)}×cos(24)cos(m6) 此处I(d)=sin(πJcw)cos(I(⊙)=cos(πJcw)sin() 通常取8-22ms,这时两个T函数值大致最大,同时又是人知的倍数,因此c0s(d)≈1 紧接着H和13C的90度脉冲产生三量子项: =4HN CgT()+4HN.C ()x cos()cos(/) 在与期间,只有3℃的化学位移被标记: .=(4HN.C cos(()+4HNC cos(;() xcos(9w4)cos(πdmd)cos(πd。-oh) 随后的回传过程产生: =Hcos(()+cos(()c()cos'()cos() 因此,每一对N,HN对应两个峰,分别是残基内及前一个残基的C:,一般而言,残 基内的峰稍为强一些,但也不是绝对的
HNCA 生物大分子波谱学原理 吴季辉
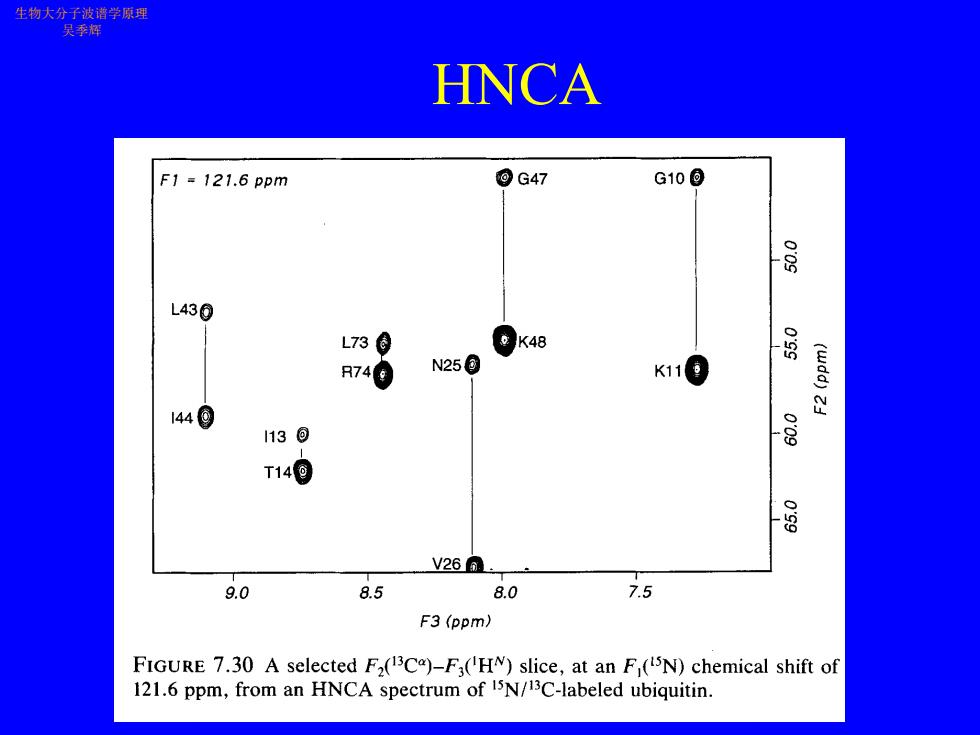
生物大分子波谱学原理 吴季辉 HNCA F1=121.6ppm ⊙G47 G10® 层 L430 L736 K48 品 R74 N250 K110 1440 113同 8 T140 8 V26D. 9.0 8.5 8.0 7.5 F3(ppm) FIGURE 7.30 A selected F2(13C)-F3(HN)slice,at an F (I5N)chemical shift of 121.6 ppm,from an HNCA spectrum of i5N/13C-labeled ubiquitin
HNCA 生物大分子波谱学原理 吴季辉