
确界原理证明 设非空集合E有一个上界y,x∈E,显然E的最小上界应该在x,y]中 寻找,记a1=x,b=y,二分[a,b],如果右边的闭区间中有E中的点, 则将这个区间记为[a2,b,],否则将左边的区间记为[a2,b,],继续二分 [a2,b],如此下去得到一列闭区间套:In=[an,b,],满足 1小4343=2neN 2、在I的右端点的右边再也没有E中的点, 3、In总包含E中的点。 由闭区间套定理立即得到B=∩I,下证B=supE 由条件2知B为E的一个上界,由条件3得到Vε>0,3x∈E,x,>B-6
确界原理证明 1 1 1 1 2 2 2 2 2 2 1 2 3 1 , [ , ] , , , , , , , , 1 , , 2 2 3 n n n n n n n E x E E x a x b a b E a b a b a b I a b x I I I I n I E I E N 设非空集合 有一个上界 , 显然 的最小上界应该在 中 寻找,记 二分 如果右边的闭区间中有 中的点, 则将这个区间记为 ,否则将左边的区间记为 ,继续二分 ,如此下去得到一列闭区间套: ,满足 、 ,且 、在 的右端点的右边再也没有 中的点, 、 总包含 中的点。 由闭 n=1 0 0 = , =sup 2 E 3 0, , n I E x E x 区间套定理立即得到 下证 由条件 知 为 的一个上界,由条件 得到

例 inf N inf0,1),sup(0,1) nr公neNp信neN inf{arctanx:x∈R},sup{arctanx:x∈R}
例 inf inf(0,1),sup(0,1) 1 1 inf , ,sup , inf arctan : ,sup arctan : n n n n x x x x N N N
例 1+了=12,3 n 1.0 00。。。o。a600.090.000°a000 0.5 0.0TTTTT1+TTTTT+TT+TTT 10 203040 50 .0.5 .1.0 00a00a0000d000d00000
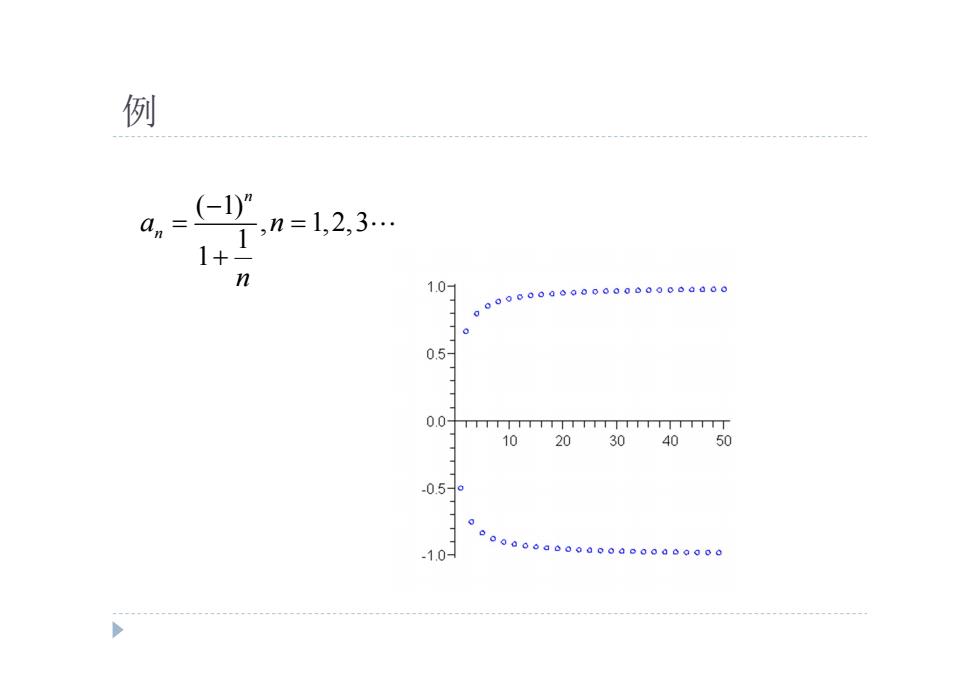
例 ( 1) , 1,2,3 1 1 n n a n n

映射 设A,B是两个集合,如果对于每一个中的元素x,B中都有唯一确定的 元素(记为f(x)与x对应,则称f是一个由A到B的映射,用f:A→B来 表示,集合A叫做映射f的定义域,f(x)∈B叫做x在f之下的象。 f:A→B,如果f(A)=B,称f是由A到B的满射 ∫:A→B,如果x,y∈A,x≠时f(x)≠fy),则称f为单射 f:A→B既是单射又是满射,则称f在A与B之间建立一一对应关系 ∫:A→B,若存在另一映射g:B→A,y∈B,由该映射g有唯一的 x∈A与y相对应,并且f(x)=y,则称f是可逆映射,记g=f f:B→C,映射g的定义域为A,当x∈A=g(B)时,定义映射 (∫·8)(x)=f(g(x),fog:A,→C称为映射f与g的复合
映射 , , ( ) ( : , ) A B A x B f x x f A B A f f f A B x B x f 设 是两个集合,如果对于每一个 中的元素 中都有唯一确定的 元素 记为 与 对应,则称 是一个由 到 的映射,用 来 表示 集合 叫做映射 的定义域, 叫做 在 之下的象。 f A B f A B f A B : ( ) , ,如果 称 是由 到 的满射 f A B x y A x y f x f y f : , , ( ) ( ) ,如果 时 ,则称 为单射 f A B f A B : 既是单射又是满射,则称 在 与 之间建立一一对应关系 1 : : , , ( ) , f A B g B A y B g x A y f x y f g f ,若存在另一映射 由该映射 有唯一的 与 相对应,并且 则称 是可逆映射,记 1 1 1 : , , ( ) ( ) ( ( )) f B C g A x A g B f g x f g x f g A C f g 映射 的定义域为 当 时,定义映射 , : 称为映射 与 的复合

映射和函数 f:A→B且g:A→B,如果x∈A,f(x)=g(x),则称f=g 如果B∈R,则称映射f:A→B为泛函 如果A,BR,则称映射f:A→B为函数,A称为f的定义域, 记作D(f),f(A)={yf=f(x),x∈A称为f的值域,记作R(f) ∫:A→A,如果x∈A,f(x)=x,则称f为恒等映射或单位映射, 记作1或1 如果函数f:A→R(f),其逆映射f1:R(f)→A,称为f的反函数
映射和函数 f A B g A B x A f x g x f g : : , , ( ) ( ), 且 如果 则称 如果B f A B , : 则称映射 为泛函 , , : ( ), ( ) ( ) , , ( ) A B f A B A f D f f A y f f x x A f R f 如果 则称映射 为 称为 的定义域, 记作 称为 的值 记作 函 域, 数 : , ( ) , A f A A x A f x x f I I ,如果 则称 为恒等映射或单位映射, 记作 或 1 f A R f f R f A f : ( ) : ( ) , 如果函数 ,其逆映射 称为 的反函数