致学模型 如何预报人口的增长 背景 世界人口增长概况 年 1625183019301960197419871999 人口(亿) 5 10 20 30 40 50 60 中国人口增长概况 年 190819331953196419821990 19952000 人口(亿) 3.04.7 6.07.210.3 11.3 12.013.0 研究人口变化规律 控制人口过快增长
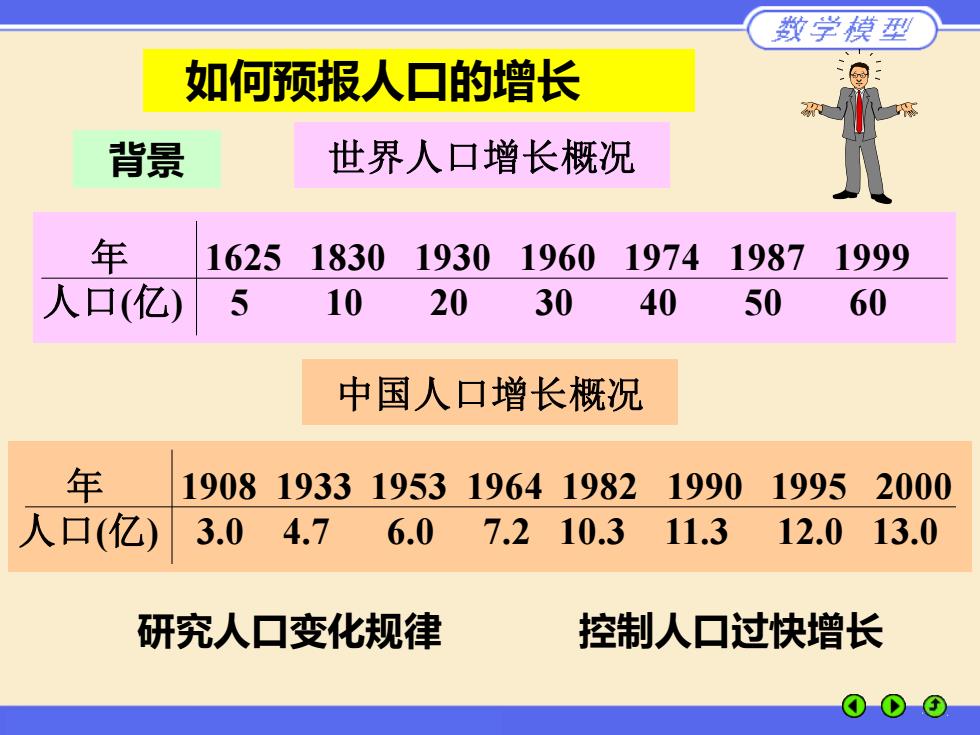
背景 年 1625 1830 1930 1960 1974 1987 1999 人口(亿) 5 10 20 30 40 50 60 世界人口增长概况 中国人口增长概况 年 1908 1933 1953 1964 1982 1990 1995 2000 人口(亿) 3.0 4.7 6.0 7.2 10.3 11.3 12.0 13.0 研究人口变化规律 控制人口过快增长 如何预报人口的增长

数学模型 常用的计算公式 今年人口xo,年增长率r k年后人口 x=x。(1+r) 指数增长模型 马尔萨斯提出(1798) 基本假设:人口(相对)增长率r是常数 x()~时刻的人口 x(t+△t)-x(t) rAt x(t) dx dt =x,x(O)=x0x(t)=x,e” x(t)=x(e)'≈x(1+r) 随着时间增加,人口按指数规律无限增长
指数增长模型——马尔萨斯提出 (1798) 常用的计算公式 k k x x (1 r) = 0 + x(t) ~时刻t的人口 基本假设 : 人口(相对)增长率 r 是常数 r t x t x t t x t = + − ( ) ( ) ( ) 今年人口 x0 , 年增长率 r k年后人口 0 rx, x(0) x dt dx = = rt x t x e0 ( ) = r t x(t) x (e ) = 0 t x (1 r) 0 + 随着时间增加,人口按指数规律无限增长

数学模型 指数增长模型的应用及局限性 ·与19世纪以前欧洲一些地区人口统计数据吻合 ·适用于19世纪后迁往加拿大的欧洲移民后代 ·可用于短期人口增长预测 ·不符合19世纪后多数地区人口增长规律 ·不能预测较长期的人口增长过程 19世纪后人口数据 人口增长率不是常数(逐渐下降)
指数增长模型的应用及局限性 • 与19世纪以前欧洲一些地区人口统计数据吻合 • 适用于19世纪后迁往加拿大的欧洲移民后代 • 可用于短期人口增长预测 • 不符合19世纪后多数地区人口增长规律 • 不能预测较长期的人口增长过程 19世纪后人口数据 人口增长率r不是常数(逐渐下降)

数学模型 阻滞增长模型(Logistic模型) 人口增长到一定数量后,增长率下降的原因: 资源、环境等因素对人口增长的阻滞作用 且阻滞作用随人口数量增加而变大)是x的减函数 假设 r(x)=r-x(r,S>O)固有增长率x很小时) xm~人口容量(资源、环境能容纳的最大数量) 之 →r(Xm)=0→S= r(x)=r(1-x m m
阻滞增长模型(Logistic模型) 人口增长到一定数量后,增长率下降的原因: 资源、环境等因素对人口增长的阻滞作用 且阻滞作用随人口数量增加而变大 假设 r(x) = r − sx (r,s 0) r~固有增长率(x很小时) xm~人口容量(资源、环境能容纳的最大数量) ( ) (1 ) m x x r x = r − r是x的减函数 xm r r(xm ) = 0 s =
数学模致 阻滞增长模型(Logistic模型) dx dx dt =r(x)x=rx(1-x) dt dxldt /2 0 Xo 七m/2 Xmx 0 x(t)= Xm x()S形曲线, 1+( 2一1 e-m x增加先快后慢
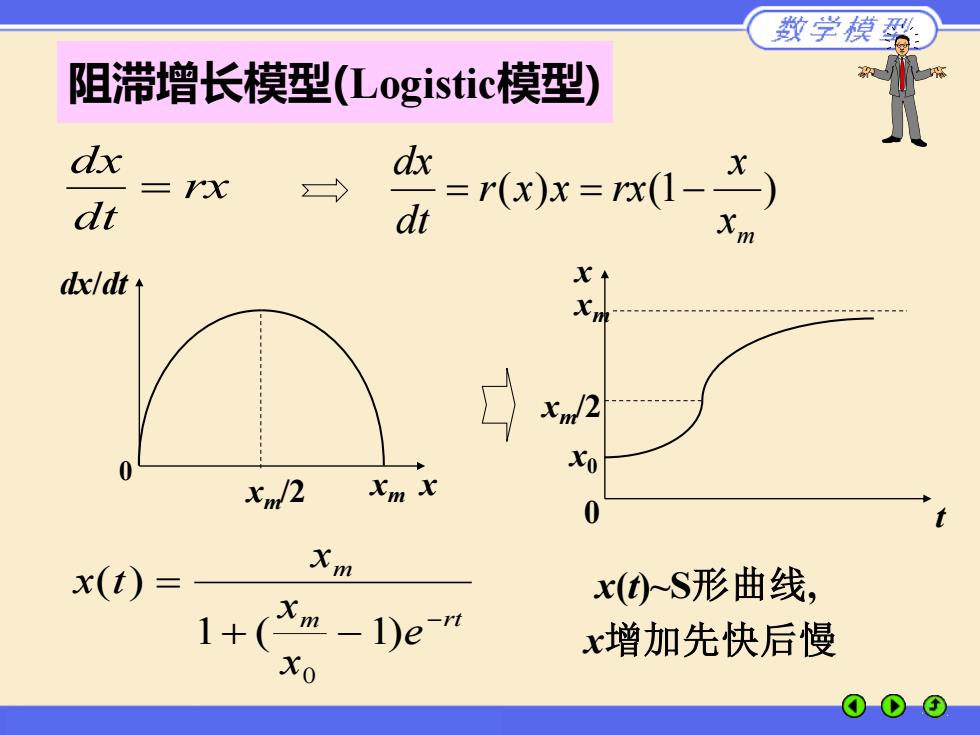
rx dt dx = ( ) (1 ) m x x r x x rx dt dx = = − dx/dt x 0 xm/2 xm xm x t x x x e m m rt ( ) ( ) = + − − 1 1 0 t x 0 x(t)~S形曲线, x增加先快后慢 x0 xm/2 阻滞增长模型(Logistic模型)