
CMOS带隙基准源研究 将式(2.1)变形代入上式(2.9)得: △Vee=Vln -V.In 12 (2.10) 1s1 =VInn (2.11) 这样,VBE的差值就表现出正温度系数: BAVeE=KInn (2.12) aT 9 可以看出,这个温度系数与温度或集电极电流的特性无关[1]。 VoD △VBE mls 图2-4发射极面积不同的PTAT电压产生电路 在图24中,我们认识到,如果两个晶体管的发射极面积不同,他们的基极 发射极电压的差值也与绝对温度成正比。忽略基极电流,我们可以得到: △VeE=VeE1-VeE2 (2.13) =VIn -v In (2.14) 1s1 mls2 =VInnm (2.15) 因此,温度系数等于(k/q)ln(nm),是一个和温度无关的常数,很好的说明了 基极-发射极电压差值与温度成正比例线性关系。 2.2.4带隙基准电压源 由下图2-5给出的带隙基准的一般原理图,我们可以看到,带隙基准电压源 的输出参考电压有两部分不同温度特性的电压组成:一部分电压与温度正相关, 另一部分电压与温度负相关。当两部分电压以适当的权重相加,则结果就会为零 温度系数。 由下图2-5可知,负温度系数电压是由室温下温度系数为-2.2mVI°C的pn结 二极管产生电压VE。正温度系数电压是产生的一个热电压V(=kTq),其与绝对 温度(PTAT)成正比,室温下的温度系数为+0.085mV°C。如果热电压V乘以常 量K加上电压VE,则输出电压为: VREF VBE +KVT (2.16) 将式(2.16)对温度求导,用V和V的温度系数求出理论上不依赖与温度的K 值。为了达到所希望的性能,更详细地分析VBE与温度的关系是必需的。因为 8
CMOS 带隙基准源研究 8 将式(2.1)变形代入上式(2.9)得: 0 0 BE T T S1 S2 ln ln nI I VV V I I (2.10) T V n ln (2.11) 这样,VBE 的差值就表现出正温度系数: BE ln V k n T q (2.12) 可以看出,这个温度系数与温度或集电极电流的特性无关[1]。 图 2–4 发射极面积不同的 PTAT 电压产生电路 在图 2-4 中,我们认识到,如果两个晶体管的发射极面积不同,他们的基极 -发射极电压的差值也与绝对温度成正比。忽略基极电流,我们可以得到: VVV BE BE1 BE2 (2.13) 0 0 T T S1 S2 ln ln nI I V V I mI (2.14) T V nm ln (2.15) 因此,温度系数等于(k/q)ln(nm),是一个和温度无关的常数,很好的说明了 基极-发射极电压差值与温度成正比例线性关系。 2.2.4 带隙基准电压源 由下图 2-5 给出的带隙基准的一般原理图,我们可以看到,带隙基准电压源 的输出参考电压有两部分不同温度特性的电压组成:一部分电压与温度正相关, 另一部分电压与温度负相关。当两部分电压以适当的权重相加,则结果就会为零 温度系数。 由下图2-5可知,负温度系数电压是由室温下温度系数为-2.2mV/°C的pn结 二极管产生电压VBE。正温度系数电压是产生的一个热电压VT(=kT/q),其与绝对 温度(PTAT)成正比,室温下的温度系数为+0.085 mV/°C。如果热电压VT乘以常 量K加上电压VBE,则输出电压为: V V KV REF BE T (2.16) 将式(2.16)对温度求导,用 VBE 和 VT 的温度系数求出理论上不依赖与温度的 K 值。为了达到所希望的性能,更详细地分析 VBE 与温度的关系是必需的。因为

第二章带隙基准源原理 V与电源几乎无关(如自举基准),所以带隙基准与电源电压几乎无关20]。 VBE /BE VREF=VBE+KVT V V VT=kT/q 图2-5带隙基准的一般原理 如下图2-6所示,VREF标示的是带隙基准电压对温度的函数曲线,VpTT标 示的是正温度系数电压对温度的函数曲线,VCTAT标示的是负温度系数电压对温 度的函数曲线。该图更加直观的表达了带隙基准源的一般原理。理想情况下,得 到的曲线是一条与温度轴平行的曲线,但是实际上,曲线的“曲率”是有限的, 也就是带隙电压的温度系数T℃在某一温度下为零,在其他温度下为正值或者负 值。在这里曲率的变化是由于基极-发射极电压、集电极电流和失调电压随温度 改变共同引起的。 VREF VREF from△VBE VPTAT VCTAT from VBE T(K) 图2-6带隙基准正负温度曲线加权 下图2-7是在不同温度下典型的带隙基准电压源电路的温度系数曲线图。综 合图2-5,图2-6和图2-7,我们可以得出这样的结论,输出参考电压是加权的 热电压和基极-发射极电压的和。因为基极-发射极电压的温度系数并不是常数, 9
第二章 带隙基准源原理 9 VBE与电源几乎无关(如自举基准),所以带隙基准与电源电压几乎无关[20]。 图 2–5 带隙基准的一般原理 如下图 2-6 所示,VREF标示的是带隙基准电压对温度的函数曲线,VPTAT标 示的是正温度系数电压对温度的函数曲线,VCTAT 标示的是负温度系数电压对温 度的函数曲线。该图更加直观的表达了带隙基准源的一般原理。理想情况下,得 到的曲线是一条与温度轴平行的曲线,但是实际上,曲线的“曲率”是有限的, 也就是带隙电压的温度系数 TC 在某一温度下为零,在其他温度下为正值或者负 值。在这里曲率的变化是由于基极-发射极电压、集电极电流和失调电压随温度 改变共同引起的。 T(K) VREF (V) vREF vCTAT vPTAT from ∆VBE from VBE 图 2–6 带隙基准正负温度曲线加权 下图 2-7 是在不同温度下典型的带隙基准电压源电路的温度系数曲线图。综 合图 2-5,图 2-6 和图 2-7,我们可以得出这样的结论,输出参考电压是加权的 热电压和基极-发射极电压的和。因为基极-发射极电压的温度系数并不是常数

CMOS带隙基准源研究 所以增益K可以通过在某一温度下使输出的温度系数为零而得到。换而言之, 热电压发生器是为了抵消基极-发射极电压对温度的线性的变化关系。抵消后, 图2-7中的输出电压由随温度非线性变化的基极-发射极电压产生。因此,我们 通常会用带隙基准源电路来弥补这种非线性,这种用来弥补带隙基准源输出参考 电压与温度非线性关系的方法被称作曲率补偿20]。 VREF(V) 1.290 To=400K 1.280 (a) 1270 OVREE =0 aT (b) T0=300K 1.260 aV旺=0 1.250 aT 124g (c) To=200K =0 aT →T(C) -40-20020406088100120 图2-7带隙基准源输出电压随温度变化曲线 2.2.5典型电路分析 图2-8所示为传统的n阱工艺CMOS带隙基准。另外,理想运算放大器的 输入失调电压(VOs)已经包含在电路中。假设晶体管Q1和Q2分别有发射区-基 区面积A和nA,同时假设VOs为零。由于运算放大器迫使下属关系成立: Vx=VY VBE1 (2.17) VoD M2 M3 VREF Vos 2 R2 图2-8一个传统的带隙基准电压源电路 10
CMOS 带隙基准源研究 10 所以增益 K 可以通过在某一温度下使输出的温度系数为零而得到。换而言之, 热电压发生器是为了抵消基极-发射极电压对温度的线性的变化关系。抵消后, 图 2-7 中的输出电压由随温度非线性变化的基极-发射极电压产生。因此,我们 通常会用带隙基准源电路来弥补这种非线性,这种用来弥补带隙基准源输出参考 电压与温度非线性关系的方法被称作曲率补偿[20]。 T(°C) VREF(V) 1.240 1.250 1.260 1.270 1.280 1.290 -40 -20 0 20 40 120 60 80 100 REF 0 V T T0=400K T0=300K T0=200K (a) (b) (c) REF 0 V T REF 0 V T 图 2–7 带隙基准源输出电压随温度变化曲线 2.2.5 典型电路分析 图 2-8 所示为传统的 n 阱工艺 CMOS 带隙基准。另外,理想运算放大器的 输入失调电压(VOS)已经包含在电路中。假设晶体管 Q1 和 Q2 分别有发射区-基 区面积 A 和 nA,同时假设 VOS 为零。由于运算放大器迫使下属关系成立: VVV X Y BE1 (2.17) 图 2–8 一个传统的带隙基准电压源电路

第二章带隙基准源原理 那么R1上的电压为: ,=Vae1-Ve2=YInn)y (2.18) 若所有PMOS管均相同,则: 6=h=2=R (2.19) 因此,图2-8的基准电压写成: Ve=Me+4R=Ve+,及) (2.20) 将式(2.17)和式(2.18)代入式(2.19),并将结果代入式(2.20)得: VREF VBE1 + )In(n)Vr (2.21) R 比较式(2.16)和式(2.21),定义常数K为: K=( )In(n) (2.22) R 于是常数K以电阻的比值和发射区-基区面积之比定义,这个结果与电阻的温度 系数无关。 如果输入失调电压不是零,那么可以证明,式(2.21)变为: aer=Vae+(径ln(nV+as] (2.23) R 显然,运算放大器的输入失调电压应该很小而且与温度无关才不会使VEF的性 能恶化。 2.3带隙基准电流源原理 在电路设计过程中,为了使电路工作在所期望的状态,就必须要对其进行直 流偏置。对于局部偏置一般使用电压偏置,而对于长距离的全局偏置一般使用电 流偏置。用于偏置的参考电流一般由2种方式产生,一种是由带隙基准核心电路 单独产生的PTAT电流,一种是由参考电压转换得到的偏置电流。 (1)PTAT电流的产生[1] 在带隙电路的分析中,我们注意到双极型晶体管的偏置电流实际上是与温度 成正比(PTAT)的。PTAT电流在许多应用中是很有效的,它可以通过图2-9所示 电路产生。它也可以用另外一种方法产生,我们可以将与电源无关的偏置电路和 双极型晶体管结合,得到图2-10的电路。 为了简单起见,假设M1~M2和M3~M4均未相同的对管,我们注意到:要 使lb1=D2,电路必须保证x=4。所以,lb1=b2=(Vlnn)/R1,结果,使lb5产生 同样地特性。在实际应用中,由于晶体管之间的不匹配,以及更重要的是由于 R的温度系数,D5的变化会偏离理想的等式。 11
第二章 带隙基准源原理 11 那么 R1上的电压为: 1 R1 BE1 BE2 T 2 ln n I VV V V I (2.18) 若所有 PMOS 管均相同,则: R1 312 1 V III R (2.19) 因此,图 2-8 的基准电压写成: 2 REF BE3 3 2 BE3 R3 1 R V V IR V V R (2.20) 将式(2.17)和式(2.18)代入式(2.19),并将结果代入式(2.20)得: 2 REF BE1 T 1 ln n R VV V R (2.21) 比较式(2.16)和式(2.21),定义常数 K 为: 2 1 ln n R K R (2.22) 于是常数 K 以电阻的比值和发射区-基区面积之比定义,这个结果与电阻的温度 系数无关。 如果输入失调电压不是零,那么可以证明,式(2.21)变为: 2 REF BE3 T OS 1 [ln n R V V VV R (2.23) 显然,运算放大器的输入失调电压应该很小而且与温度无关才不会使 VREF 的性 能恶化。 2.3 带隙基准电流源原理 在电路设计过程中,为了使电路工作在所期望的状态,就必须要对其进行直 流偏置。对于局部偏置一般使用电压偏置,而对于长距离的全局偏置一般使用电 流偏置。用于偏置的参考电流一般由 2 种方式产生,一种是由带隙基准核心电路 单独产生的 PTAT 电流,一种是由参考电压转换得到的偏置电流。 (1) PTAT 电流的产生[1] 在带隙电路的分析中,我们注意到双极型晶体管的偏置电流实际上是与温度 成正比(PTAT)的。PTAT 电流在许多应用中是很有效的,它可以通过图 2-9 所示 电路产生。它也可以用另外一种方法产生,我们可以将与电源无关的偏置电路和 双极型晶体管结合,得到图 2-10 的电路。 为了简单起见,假设 M1~M2 和 M3~M4 均未相同的对管,我们注意到:要 使 ID1=ID2,电路必须保证 VX=VY。所以,ID1=ID2=(VTlnn)/R1,结果,使 ID5产生 同样地特性。在实际应用中,由于晶体管之间的不匹配,以及更重要的是由于 R1的温度系数,ID5的变化会偏离理想的等式
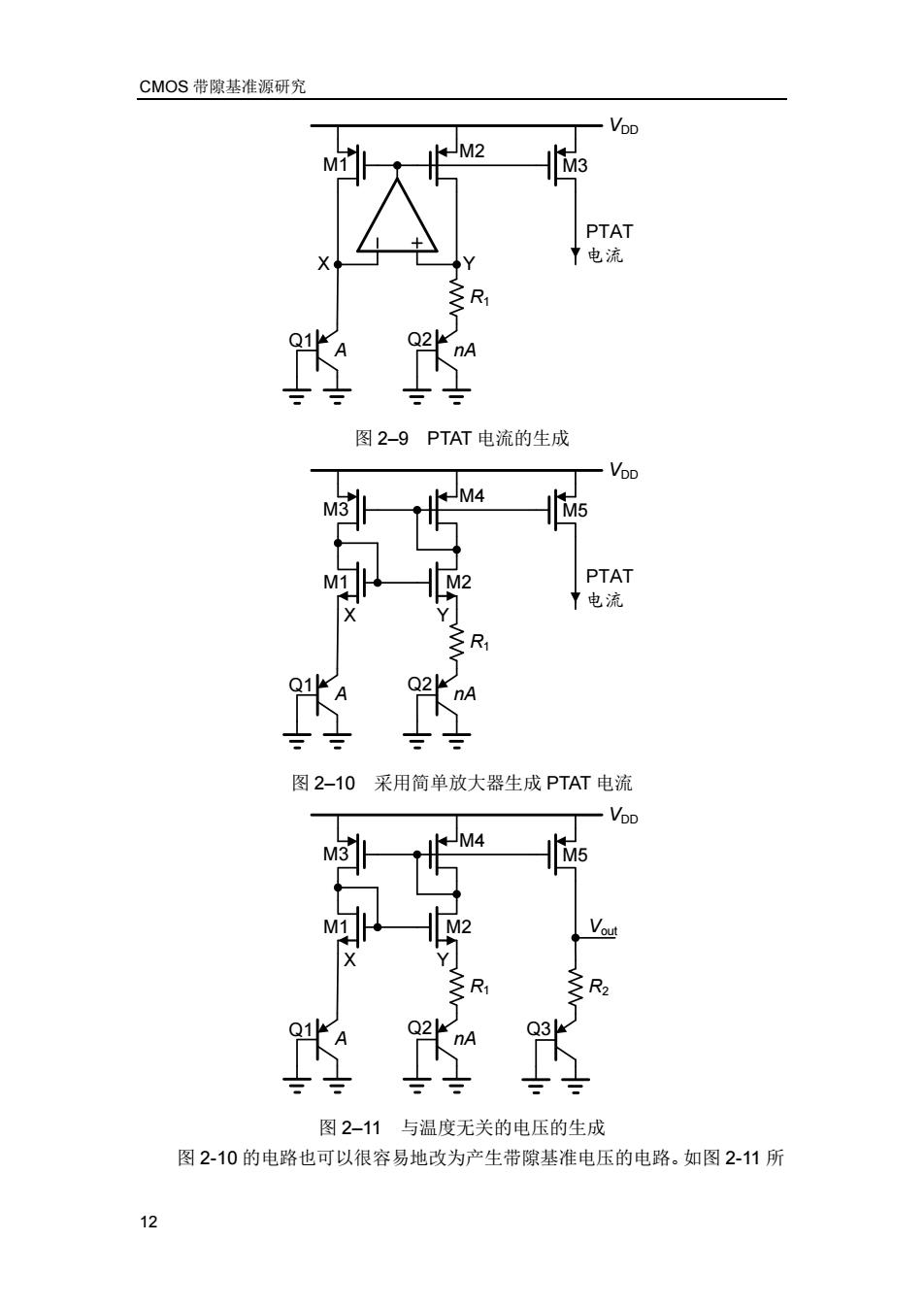
CMOS带隙基准源研究 M2 M3 PTAT 中电流 R 图2-9PTAT电流的生成 M4 M5 PTAT 【电流 nA 图2-10 采用简单放大器生成PTAT电流 VpD M4 M5 Vout R R2 Q2 Q3 图2-11与温度无关的电压的生成 图2-10的电路也可以很容易地改为产生带隙基准电压的电路。如图2-11所 12
CMOS 带隙基准源研究 12 Q2 R1 M2 M1 Q1 M3 VDD X Y A nA PTAT 电流 图 2–9 PTAT 电流的生成 Q2 R1 M4 M3 Q1 M5 VDD A nA PTAT 电流 X Y M1 M2 图 2–10 采用简单放大器生成 PTAT 电流 Q2 R1 M4 M3 Q1 M5 VDD A nA X Y M1 M2 Q3 R2 Vout 图 2–11 与温度无关的电压的生成 图 2-10 的电路也可以很容易地改为产生带隙基准电压的电路。如图 2-11 所