复旦大学：《集成电路工程》教学资源（硕士士学位论文）CMOS带隙基准源研究

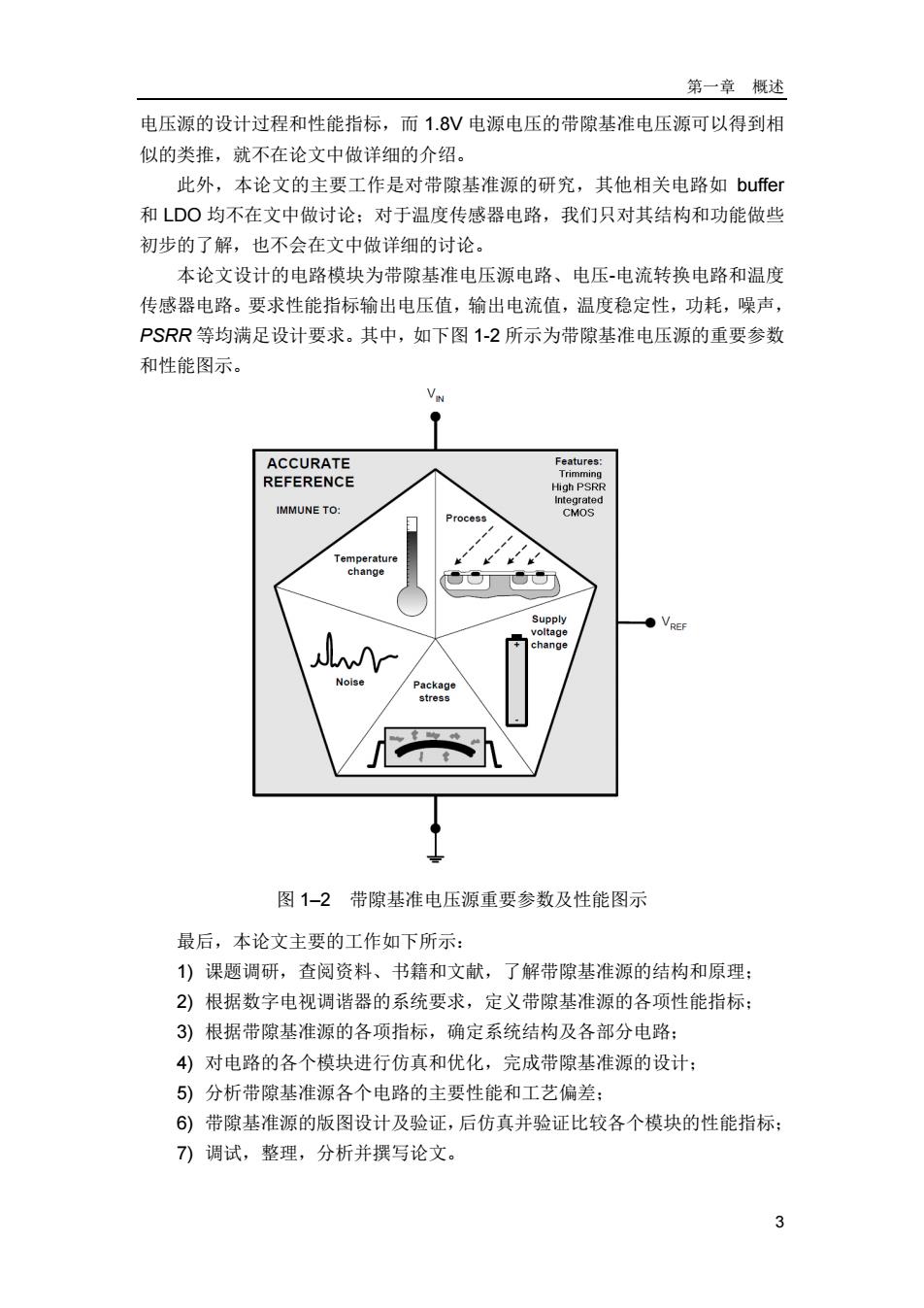
第一章概述 电压源的设计过程和性能指标，而1.8V电源电压的带隙基准电压源可以得到相 似的类推，就不在论文中做详细的介绍。 此外，本论文的主要工作是对带隙基准源的研究，其他相关电路如buffer 和LDO均不在文中做讨论：对于温度传感器电路，我们只对其结构和功能做些 初步的了解，也不会在文中做详细的讨论。 本论文设计的电路模块为带隙基准电压源电路、电压-电流转换电路和温度 传感器电路。要求性能指标输出电压值，输出电流值，温度稳定性，功耗，噪声， PSRR等均满足设计要求。其中，如下图1-2所示为带隙基准电压源的重要参数 和性能图示。 VN ACCURATE Features: Trimming REFERENCE High PSRR Integrated IMMUNE TO: Process CMOS Temperature change Supply voltage ●VREF M change Noise Package stress 图1-2带隙基准电压源重要参数及性能图示 最后，本论文主要的工作如下所示： 1)课题调研，查阅资料、书籍和文献，了解带隙基准源的结构和原理： 2)根据数字电视调谐器的系统要求，定义带隙基准源的各项性能指标： 3)根据带隙基准源的各项指标，确定系统结构及各部分电路： 4)对电路的各个模块进行仿真和优化，完成带隙基准源的设计： 5)分析带隙基准源各个电路的主要性能和工艺偏差： 6)带隙基准源的版图设计及验证，后仿真并验证比较各个模块的性能指标： 7)调试，整理，分析并撰写论文。 0

第一章 概述 3 电压源的设计过程和性能指标，而 1.8V 电源电压的带隙基准电压源可以得到相 似的类推，就不在论文中做详细的介绍。 此外，本论文的主要工作是对带隙基准源的研究，其他相关电路如 buffer 和 LDO 均不在文中做讨论；对于温度传感器电路，我们只对其结构和功能做些 初步的了解，也不会在文中做详细的讨论。 本论文设计的电路模块为带隙基准电压源电路、电压-电流转换电路和温度 传感器电路。要求性能指标输出电压值，输出电流值，温度稳定性，功耗，噪声， PSRR 等均满足设计要求。其中，如下图 1-2 所示为带隙基准电压源的重要参数 和性能图示。 图 1–2 带隙基准电压源重要参数及性能图示 最后，本论文主要的工作如下所示： 1) 课题调研，查阅资料、书籍和文献，了解带隙基准源的结构和原理； 2) 根据数字电视调谐器的系统要求，定义带隙基准源的各项性能指标； 3) 根据带隙基准源的各项指标，确定系统结构及各部分电路； 4) 对电路的各个模块进行仿真和优化，完成带隙基准源的设计； 5) 分析带隙基准源各个电路的主要性能和工艺偏差； 6) 带隙基准源的版图设计及验证，后仿真并验证比较各个模块的性能指标； 7) 调试，整理，分析并撰写论文

基准电压源和线性稳压器的设计 1.3论文组织结构 本论文分为七章深入的讨论和研究了带隙基准源电路系统的设计。详细的论 文组织结构安排如下： 第一章为概述。主要介绍课题背景、论文主要工作和论文组织结构。 第二章主要介绍了带隙基准源的基本结构和原理。详细的阐述了带隙基准电 压源的正、负温度系数电压加权叠加以及带隙基准电流源的实现方法。 第三章主要介绍了带隙基准电压源的结构、性能分析和仿真结果。其中，首 先介绍了带隙基准电压源的主要性能指标并给出了指标的定义：然后阐述了整个 带隙基准电压源电路的电路结构和设计过程：最后分析了带隙基准电压源的性能 并进行了仿真验证和总结。 第四章和第五章分别介绍了带隙基准电流源电路和温度传感器电路的结构、 简单分析及仿真结果。首先，两章分别简单分析了电路的结构及性能：然后，论 文给出了电路相应的仿真结果；最后，分别对电路进行了总结。 第六章主要介绍了整个带隙基准源电路的各个模块的版图设计及后仿验证， 最后给出了一些关于版图设计技巧的总结。 第七章在本文的最后，对整个带隙基准源的设计进行了总结和展望。 4

基准电压源和线性稳压器的设计 4 1.3 论文组织结构 本论文分为七章深入的讨论和研究了带隙基准源电路系统的设计。详细的论 文组织结构安排如下： 第一章为概述。主要介绍课题背景、论文主要工作和论文组织结构。 第二章主要介绍了带隙基准源的基本结构和原理。详细的阐述了带隙基准电 压源的正、负温度系数电压加权叠加以及带隙基准电流源的实现方法。 第三章主要介绍了带隙基准电压源的结构、性能分析和仿真结果。其中，首 先介绍了带隙基准电压源的主要性能指标并给出了指标的定义；然后阐述了整个 带隙基准电压源电路的电路结构和设计过程；最后分析了带隙基准电压源的性能 并进行了仿真验证和总结。 第四章和第五章分别介绍了带隙基准电流源电路和温度传感器电路的结构、 简单分析及仿真结果。首先，两章分别简单分析了电路的结构及性能；然后，论 文给出了电路相应的仿真结果；最后，分别对电路进行了总结。 第六章主要介绍了整个带隙基准源电路的各个模块的版图设计及后仿验证， 最后给出了一些关于版图设计技巧的总结。 第七章在本文的最后，对整个带隙基准源的设计进行了总结和展望

第二章带隙基准源原理 第二章 带隙基准源原理 2.1前言 模拟电路广泛地包含电压基准和电流基准。这种基准是直流量，它与电源和 工艺参数的关系很小，但与温度的关系是确定的。尽管在一次通过(irst-pass)模 拟设计中常常被忽视，但是毫无疑问直流电压和电流基准的性能直接影响整个电 路的所有性能。 REF VREF 图2-1理想电流和电压的伏安特性曲线 理想的基准电压或电流是与电源和温度变化无关的。图2-1所示为理想基准 电压和电流的大信号伏安特性。这些特性与理想电压源和电流源是相同的。当电 压和电流的值比在一般的源中所要求的更精确和更稳定时，这些源就冠以“基准” 的名称。典型的基准与连接到它的负载有关。一般总可以用缓冲放大器隔离基准 与负载，保持基准的高性能[16]。 2.2带隙基准电压源原理 2.2.1概述 理想情况下，电压基准提供一个己知幅度但不随温度变化的稳定直流电压。 我们有很多方法可以用于实现这种理想中的电压基准。它们包括： 1.利用齐纳二极管稳压到一个己知电压值 2.利用增强型和耗尽型晶体管阈值电压的差值 3.利用PTAT电路的正温度系数抵消pn结的负温度系数 第一种方法早已不在流行，因为对于当下的集成电路能耗来说齐纳二极管的 击穿电压实在太大了。而当耗尽型晶体管不可用时，第二种方法也就不可用，这 种情况常常发生。此外，尽管用耗尽型晶体管能够得到非常稳定的基准，但是由 于增强型和耗尽型晶体管阈值电压对工艺灵敏度的不同，这个基准的实际值是非

第二章 带隙基准源原理 5 第二章 带隙基准源原理 2.1 前言 模拟电路广泛地包含电压基准和电流基准。这种基准是直流量，它与电源和 工艺参数的关系很小，但与温度的关系是确定的。尽管在一次通过(first-pass)模 拟设计中常常被忽视，但是毫无疑问直流电压和电流基准的性能直接影响整个电 路的所有性能。 图 2–1 理想电流和电压的伏安特性曲线 理想的基准电压或电流是与电源和温度变化无关的。图 2-1 所示为理想基准 电压和电流的大信号伏安特性。这些特性与理想电压源和电流源是相同的。当电 压和电流的值比在一般的源中所要求的更精确和更稳定时，这些源就冠以“基准” 的名称。典型的基准与连接到它的负载有关。一般总可以用缓冲放大器隔离基准 与负载，保持基准的高性能[16]。 2.2 带隙基准电压源原理 2.2.1 概述 理想情况下，电压基准提供一个已知幅度但不随温度变化的稳定直流电压。 我们有很多方法可以用于实现这种理想中的电压基准。它们包括： 1． 利用齐纳二极管稳压到一个已知电压值 2． 利用增强型和耗尽型晶体管阈值电压的差值 3． 利用 PTAT 电路的正温度系数抵消 pn 结的负温度系数 第一种方法早已不在流行，因为对于当下的集成电路能耗来说齐纳二极管的 击穿电压实在太大了。而当耗尽型晶体管不可用时，第二种方法也就不可用，这 种情况常常发生。此外，尽管用耗尽型晶体管能够得到非常稳定的基准，但是由 于增强型和耗尽型晶体管阈值电压对工艺灵敏度的不同，这个基准的实际值是非

CMOS带隙基准源研究 常难以精准确定的。由于这些原因，前两种方法我们在这里就不予讨论了。最后 一种方法，不管是双极型技术还是CMOS技术，都是一种主流方法，也是我们 的主要讨论对象。而基于最后这种方法的电压基准通常被称为“带隙基准”[17刀。 由第三种方法可以将两个具有相反温度系数的量以适当的权重相加，得到与 温度关系很小的电压或电流基准，这种基准也被证实在许多模拟电路中是必不可 少的。值得注意的是，因为大多数工艺参数是随着温度变化的，所以如果一个基 准是与温度无关的，那么通常它也是与工艺无关的。 现在我们先识别具有正温度系数和负温度系数的两种电压。在半导体工艺的 各种不同器件参数中，双极晶体管的特性参数被证实具有最好的的重复性，并且 具有能提供正温度系数和负温度系数的、严格定义的量。尽管MOS器件的许多 参数已被考虑用于基准产生[18[19]，但是双极电路还是形成这类电路的核心。 2.2.2负温度系数电压 双极型晶体管的基极-发射极电压，或者更一般的说，p结二极管的正向电 压，具有负温度系数。我们首先根据容易得到的量推出温度系数的表达式。 VDD 图2-2负温度系数电压 对于恒定电流驱动，该二极管受温度影响非常大，约为-2VC,我们想把 该值将到1/1000以下。为了实现这一目标，需要一个明确表示温度关系的电流 表达式。对于一个双极器件，它的电流-电压表达式可用指数形式精确地给出： VBE Ic=Is exp KT/q (2.1) 或者用绝对零度是二极管电压给出： Vee-Va) lc=CT exp(KT/q (2.2) 对于式(2.1)，其中V-kT1q,饱和电流s正比于kTn2,其中μ为少数载流 子的迁移率，n为硅的本征载流子浓度。这些参数与温度的关系可以表示为∝ om,其中m≈-32，并且n2∝3exp[-Eg/kl,其中Eg≈1.12eV,为硅的带隙 能量。所以 Is =bT4m exp- -Eo (2.3) 6

CMOS 带隙基准源研究 6 常难以精准确定的。由于这些原因，前两种方法我们在这里就不予讨论了。最后 一种方法，不管是双极型技术还是 CMOS 技术，都是一种主流方法，也是我们 的主要讨论对象。而基于最后这种方法的电压基准通常被称为“带隙基准”[17]。 由第三种方法可以将两个具有相反温度系数的量以适当的权重相加，得到与 温度关系很小的电压或电流基准，这种基准也被证实在许多模拟电路中是必不可 少的。值得注意的是，因为大多数工艺参数是随着温度变化的，所以如果一个基 准是与温度无关的，那么通常它也是与工艺无关的。 现在我们先识别具有正温度系数和负温度系数的两种电压。在半导体工艺的 各种不同器件参数中，双极晶体管的特性参数被证实具有最好的的重复性，并且 具有能提供正温度系数和负温度系数的、严格定义的量。尽管 MOS 器件的许多 参数已被考虑用于基准产生[18][19]，但是双极电路还是形成这类电路的核心。 2.2.2 负温度系数电压 双极型晶体管的基极-发射极电压，或者更一般的说，pn 结二极管的正向电 压，具有负温度系数。我们首先根据容易得到的量推出温度系数的表达式。 图 2–2 负温度系数电压 对于恒定电流驱动，该二极管受温度影响非常大，约为-2 mV/°C，我们想把 该值将到 1/1000 以下。为了实现这一目标，需要一个明确表示温度关系的电流 表达式。对于一个双极器件，它的电流-电压表达式可用指数形式精确地给出： BE C S exp k q V I I T  (2.1) 或者用绝对零度是二极管电压给出： BE g0 C C exp k q η V V I T T     (2.2) 对于式(2.1)，其中 VT=kT/q，饱和电流 IS正比于 μkTni 2 ，其中 μ 为少数载流 子的迁移率，ni 为硅的本征载流子浓度。这些参数与温度的关系可以表示为 μ∝ μ0Tm，其中 m≈-3/2，并且 ni 2 ∝T3 exp[-Eg/(kT)]，其中 Eg≈1.12eV，为硅的带隙 能量。所以 4 S exp k m Eg I bT T    (2.3)

第二章带隙基准源原理 其中b是一个比例系数。写出Ve=V-ln(los),我们现在就可以计算基极-发射极 电压的温度系数了。在VE对T取导数时，我们一定知道1c也是温度的函数。 为了简化分析，我们暂时假设6保持不变。这样 aYe=aYn-业n' (2.4) aT OT ls als T 由式(2.3)我们有 是-b4 m导+br*ep导导 (2.5) 所以 Y=(4+m)T+K V E (2.6) Is OT 由式(2.4)和式(2.6)，我们可以得到 器-兰n%-am片导4 (2.7） VBE-(4+m)v-Eg/q (2.8) T 等式(2.8)给出了温度T下基极-发射极电压的温度系数，从中可以看到，它与VE 本身的大小有关。当VBe≈750mV,T=300K时，8VBE/aT≈-1.5mVK1]。 由式(28)可以看出，分子中后两项之和比基极-发射极电压要大，所以其值 是一个与温度和基极-发射极电压相关的负值，表示基极-发射极电压的温度系数 曲线是一条斜率为负的非线性曲线。 2.2.3正温度系数电压 在1964年人们就认识到，如果两个双极晶体管工作在不相等的电流密度下， 那么他们的基极-发射极电压的差值就与绝对温度成正比。例如，图2-3所示， 如果两个同样地晶体管(s1=s2)偏置的集电极分别为lo和6并忽略它们的基极 电流。 图2-3PTAT电压产生电路 那么，基极-发射极电压的差值为： AVBE VBE1-VBE2 (2.9)

第二章 带隙基准源原理 7 其中 b 是一个比例系数。写出 VBE=VTln(IC/IS)，我们现在就可以计算基极-发射极 电压的温度系数了。在 VBE 对 T 取导数时，我们一定知道 IC 也是温度的函数。 为了简化分析，我们暂时假设 IC保持不变。这样 BE T T C S S S ln ln VV V I I T TI I T        (2.4) 由式(2.3)我们有 S 3 4 2 ( +m) exp (exp )( ) k kk I m m E EE g gg b T bT T T TT         4 (2.5) 所以 T T S 2 T S (4 ) k V V I Eg m V IT T T     (2.6) 由式(2.4)和式(2.6)，我们可以得到 BE T T C 2 T S ln (4 ) k Eg VV V I m V T TI T T      (2.7) BE T (4 ) V mV E q g T     (2.8) 等式(2.8)给出了温度 T 下基极-发射极电压的温度系数，从中可以看到，它与 VBE 本身的大小有关。当 VBE≈750 mV，T=300 K 时， VBE/  T≈-1.5 mV/K[1]。 由式(2.8)可以看出，分子中后两项之和比基极-发射极电压要大，所以其值 是一个与温度和基极-发射极电压相关的负值，表示基极-发射极电压的温度系数 曲线是一条斜率为负的非线性曲线。 2.2.3 正温度系数电压 在 1964 年人们就认识到，如果两个双极晶体管工作在不相等的电流密度下， 那么他们的基极-发射极电压的差值就与绝对温度成正比。例如，图 2-3 所示， 如果两个同样地晶体管(IS1=IS2)偏置的集电极分别为 nI0 和 I0 并忽略它们的基极 电流。 图 2–3 PTAT 电压产生电路 那么，基极-发射极电压的差值为： VVV BE BE1 BE2   (2.9)