
试验设计与分析 试验结果分析 因为S4与S相互独立(证明略),再由x分布的可加性性质可得出 0-” 并得出S4的自由度为(r1)。 记 r-1 '。= n-r 并分别叫做S4,S的均方。由此可知,',是o2的无偏估计,当H成立时,'4也是σ2的 无偏估计。 在成立的条件下,取统计量 F- x--Fr-1,n-), S. /n-r 即 F=-F0-1-
试验设计与分析 试验结果分析
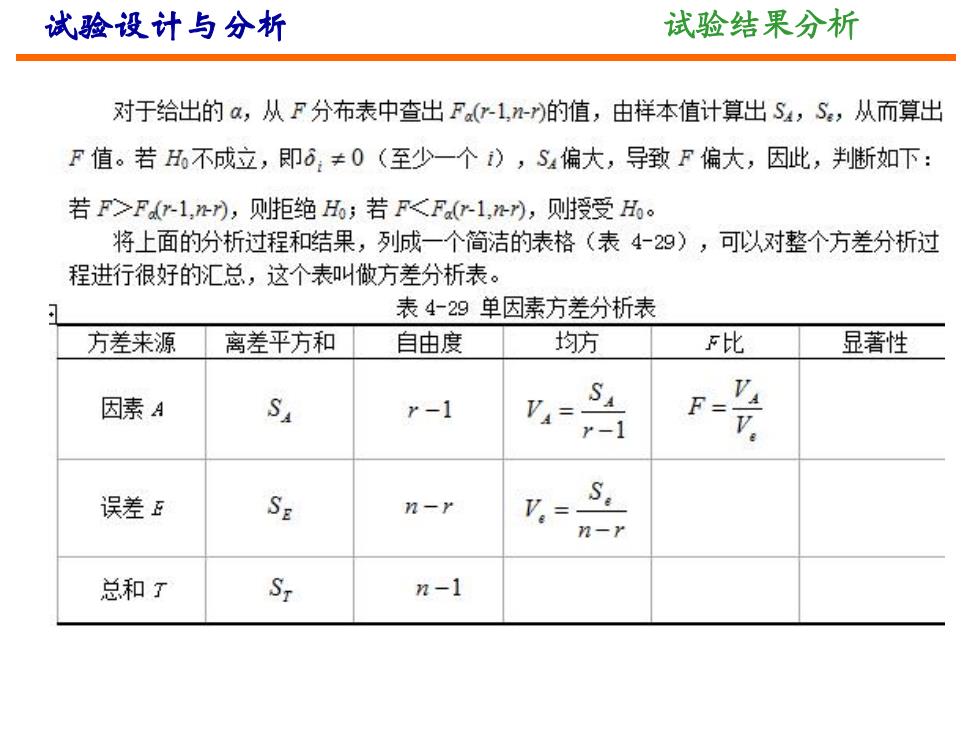
试验设计与分析 试验结果分析 对于给出的a,从F分布表中查出F(r-1,n-的值,由样本值计算出S4,S,从而算出 F值。若H不成立,即6:≠0(至少一个i),S偏大,导致F偏大,因此,判断如下: 若F>Fr-1,),则拒绝o;若F<Fr-1,),则授受。 将上面的分析过程和结果,列城一个简洁的表格(表4-29),可以对整个方差分析过 程进行很好的汇总,这个表叫做方差分析表。 表4-29单因素方差分析表 方差来源 离差平方和 自由度 均方 F比 显著性 因素A S r-1 4= F= r-1 误差正 SE n-r n.=5, n-r 总和了 Si n-1
试验设计与分析 试验结果分析
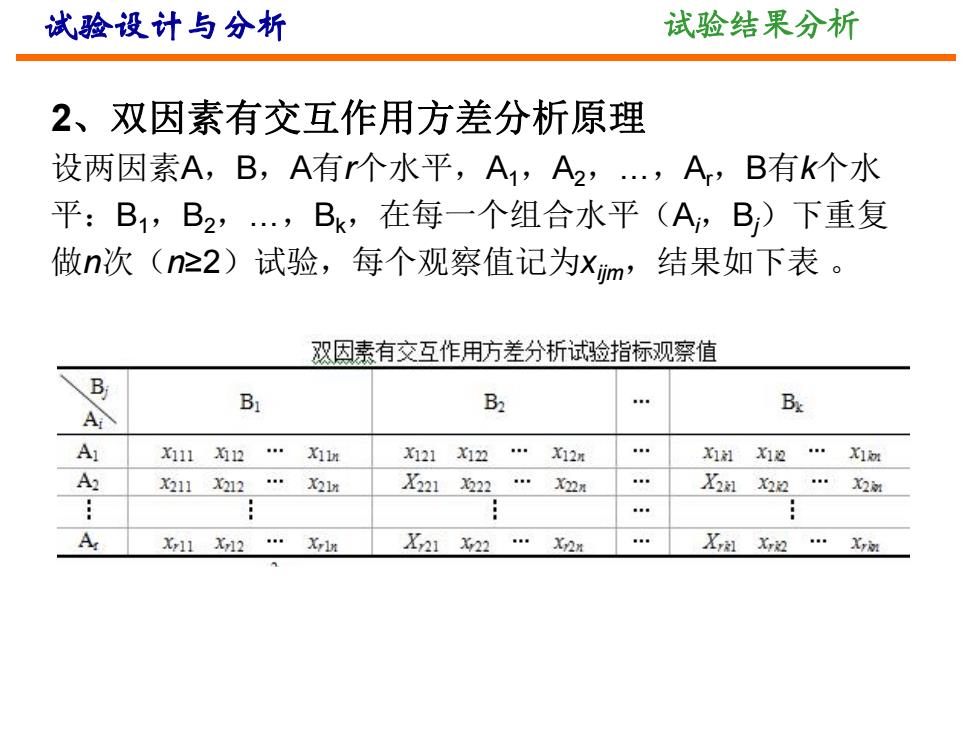
试验设计与分析 试验结果分析 2、双因素有交互作用方差分析原理 设两因素A,B,A有r个水平,A1,A2,.,A,B有k个水 平:B1,B2,.,Bk,在每一个组合水平(A,B)下重复 做n次(n22)试验,每个观察值记为xm'结果如下表。 双因素有交互作用方差分析试验指标观察值 B B1 B … Bx A A X灯11为12…灯r X21X灯2…X2m … xX1别X1边…X1m A2 X11X212… X2 X322122… X2n … X21X32…X2耐 。 A X11X12… Xrln X21x22…X2m X的X2…
试验设计与分析 试验结果分析 2、双因素有交互作用方差分析原理 设两因素A,B,A有r个水平,A1,A2,…,Ar,B有k个水 平:B1,B2,…,Bk,在每一个组合水平(Ai,Bj)下重复 做n次(n≥2)试验,每个观察值记为xijm,结果如下表

试验设计与分析 试验结果分析 设xw~N(40),各x之间相互独立,=1,2,…,1,户1,2,…,k,m=1,2,…, 血,各m相互独立。 并设 4g=4+a:+B,+Y 其中4为总平均值,为水平A的效应,月为水平B的效应,为水平A:和水平B的交互 效应,显然有 含a=0,实月=0,2%=0,=0 我们取下面的线性统计模型 xw=u+a:+B,+Y指+8m em~N(0.o2) 其中各8相互独立;=1,2,…,rj=1,2,…,k,m=1,2,…,n;,,月,,G2 都是未知参数
试验设计与分析 试验结果分析

试验设计与分析 试验结果分析 对这个线性模型,我们检验如下假设 H40:a1=a2=…=a,=0 Hn:a:≠0,至少-个i了1 Hm:月=月=…=B=01 Hm:B≠0,至少一个) H48m7i=0,i=12…,yj=12.…,k Hm:Y:≠0,至少一对,j 1、总离差平方和的分解 记
试验设计与分析 试验结果分析