
《概率论与数理统计》课程教学大纲 一、课程信息 课程名称:概率论与数理统计 Probability and Statistics 课程代码: 课程类别:专业拓展平台课程/选修课 适用专业:工程管理专业 课程学时:54学时 课程学分:2学分 修读学期:第3学期 先修课程:高等数学A(I)、高等数学A(I) 二、课程目标 (一)具体目标 通过本课程的学习,使学生达到以下目标: 课程目标1:掌握概率论基本概念,包括频率、概率、古典概型、条件概率等概 念及运算方法,会使用全概率公式以及贝叶斯公式进行计算,并能分析变量之间的独 立性;掌握离散型随机变量的分布律分布函数,包括两点分布、二项分布的分布律 分布函数:掌握连续型随机变量的概率密度包括均匀分布、指数分布、正态分布:掌 握二维随机变量边缘分布函数的定义以及边缘概率密度的计算方法。【支撑毕业要求 11】 课程目标2:掌握数学期望、方差、协方差、相关系数的计算方法;熟悉辛钦大 数定律、伯努利大数定律的使用:掌握独立同分布的中心极限定理、李雅普诺夫定理 以及棣莫弗-拉普拉斯定理的使用;掌握样本和抽样分布相关概念,能利用直方图与 箱线图解决问题;掌握矩估计量、矩估计值、似然函数、最大似然估计值、最大似然 估计量、对数似然方程的定义:熟悉假设检验相关知识,能使用正态总体均值的假设 检验。【支撑毕业要求2.1】 (二)课程目标与毕业要求的对应关系 表1课程目标与毕业要求的对应关系 1
——1—— 《概率论与数理统计》课程教学大纲 一、课程信息 课程名称:概率论与数理统计 Probability and Statistics 课程代码: 课程类别:专业拓展平台课程/选修课 适用专业:工程管理专业 课程学时:54学时 课程学分:2学分 修读学期:第3学期 先修课程:高等数学A(I)、高等数学A(II) 二、课程目标 (一)具体目标 通过本课程的学习,使学生达到以下目标: 课程目标 1:掌握概率论基本概念,包括频率、概率、古典概型、条件概率等概 念及运算方法,会使用全概率公式以及贝叶斯公式进行计算,并能分析变量之间的独 立性;掌握离散型随机变量的分布律分布函数,包括两点分布、二项分布的分布律、 分布函数;掌握连续型随机变量的概率密度包括均匀分布、指数分布、正态分布;掌 握二维随机变量边缘分布函数的定义以及边缘概率密度的计算方法。【支撑毕业要求 1.1】 课程目标 2:掌握数学期望、方差、协方差、相关系数的计算方法;熟悉辛钦大 数定律、伯努利大数定律的使用;掌握独立同分布的中心极限定理、李雅普诺夫定理 以及棣莫弗-拉普拉斯定理的使用;掌握样本和抽样分布相关概念,能利用直方图与 箱线图解决问题;掌握矩估计量、矩估计值、似然函数、最大似然估计值、最大似然 估计量、对数似然方程的定义;熟悉假设检验相关知识,能使用正态总体均值的假设 检验。【支撑毕业要求 2.1】 (二)课程目标与毕业要求的对应关系 表1 课程目标与毕业要求的对应关系
课短目标 支排的毕业要求 支排的单业要求指标底 1工程知识:能够将数学 课程标】 自些科学、工柱基和 1.1具备解决复杂工问题所需的数学、物理等自然科 业知识用于解决复杂工程 学知识和应用能力。 问题。 2问题分析:能够应用数 草、自城科学和工程科 课目标2 的本原理,识别、表达 21能够应用数学、自然科学和工柱科学的基本原理 并通过文就研究分祈复 识别与归纳复杂工程问题 工程问题,以获得有效结 论。 三、课程内容 (一)课程内容与课程目标的关系 表2课程内容与课程目标的关系 课狂内容 教学方法 支撑的课程目标 学时安排 第一章概率论的基本概念 诉投法 课柱日标1 6 第二章随机变量及其分布 讲投法 深日标1 8 第三章多推随机变量及其分布 讲投法 课程目标1、2 8 第四拿随机变童的数字特征 讲投法 课程日标1、2 8 第五章大数定律及中心极限定理 讲投法 谋在目标1 8 第六章样布及抽样分布 讲投法 课程目标1、2 4 第七章泰数估计 游投法 课程目标1、2 4 第八章低说检验 讲授法 课在目标1、2 4 合计 54学时 (二)具体内容 第一章概率论的基本概念 【学习目标】 1了解随机现象、随机试验、样本空间、随机事件的概念,掌握随机事件之间的 关系及运算: 2.了解随机事件的频率及概率的统计定义和基本性质: 3.学握古典概型定义: 4理解条件概率的定义,掌握乘法公式、全概率公式和贝叶斯公式:
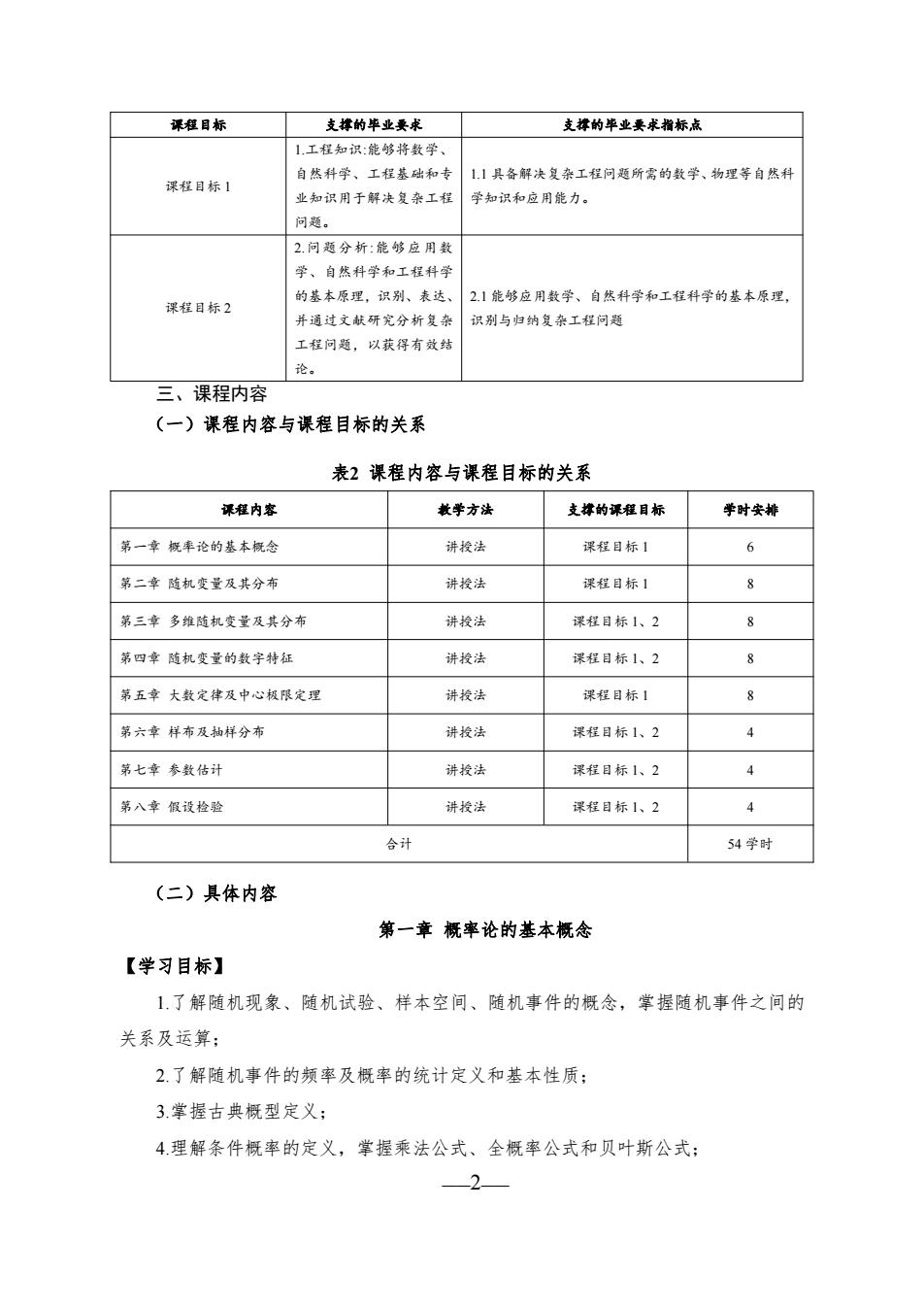
——2—— 课程目标 支撑的毕业要求 支撑的毕业要求指标点 课程目标 1 1.工程知识:能够将数学、 自然科学、工程基础和专 业知识用于解决复杂工程 问题。 1.1 具备解决复杂工程问题所需的数学、物理等自然科 学知识和应用能力。 课程目标 2 2.问题分析:能够应用数 学、自然科学和工程科学 的基本原理,识别、表达、 并通过文献研究分析复杂 工程问题,以获得有效结 论。 2.1 能够应用数学、自然科学和工程科学的基本原理, 识别与归纳复杂工程问题 三、课程内容 (一)课程内容与课程目标的关系 表2 课程内容与课程目标的关系 课程内容 教学方法 支撑的课程目标 学时安排 第一章 概率论的基本概念 讲授法 课程目标 1 6 第二章 随机变量及其分布 讲授法 课程目标 1 8 第三章 多维随机变量及其分布 讲授法 课程目标 1、2 8 第四章 随机变量的数字特征 讲授法 课程目标 1、2 8 第五章 大数定律及中心极限定理 讲授法 课程目标 1 8 第六章 样布及抽样分布 讲授法 课程目标 1、2 4 第七章 参数估计 讲授法 课程目标 1、2 4 第八章 假设检验 讲授法 课程目标 1、2 4 合计 54 学时 (二)具体内容 第一章 概率论的基本概念 【学习目标】 1.了解随机现象、随机试验、样本空间、随机事件的概念,掌握随机事件之间的 关系及运算; 2.了解随机事件的频率及概率的统计定义和基本性质; 3.掌握古典概型定义; 4.理解条件概率的定义,掌握乘法公式、全概率公式和贝叶斯公式;

5.理解随机事件独立性的概念,掌握利用事件独立性进行计算。 【学习内容】 1.随机试验 2.随机事件的概率 3.古典概型; 4.条件概率: 5.事件的独立性: 【学习重点】 1随机事件: 2.概率的基本性质及其应用: 3乘法定理、全概率公式与贝叶斯公式: 4.事件的独立性。 【学习难点】 1概率的公理化定义: 2.条件概率概念的建立: 3.全概率公式与贝叶斯公式的应用。 第二章随机变量及其分布 【学习目标】 1理解随机交量的定义,了解用随机变量表示随机事件: 2.了解分布函数的定义及其性质,会利用分布函数计算事件的概率; 3.理解离散型随机变量及其分布列的定义、性质,掌握离散型随机变量的分布律 及分布函数 4.掌握常见的离散型随机变量的分布的概率分布:两点分布、二项分布、泊松分 布: 5理解连续型随机变量及概率密度的定义、性质掌握用密度函数计算概率,掌握 常见的连续型随机变量概率计算:均匀分布、指数分布和正态分布: 6.了解随机变量函数的概念,了解随机变量的简单函数的分布的求法。 【学习内容】 1.随机变量 3
——3—— 5.理解随机事件独立性的概念,掌握利用事件独立性进行计算。 【学习内容】 1.随机试验; 2.随机事件的概率; 3.古典概型; 4.条件概率; 5.事件的独立性; 【学习重点】 1.随机事件; 2.概率的基本性质及其应用; 3.乘法定理、全概率公式与贝叶斯公式; 4.事件的独立性。 【学习难点】 1.概率的公理化定义; 2.条件概率概念的建立; 3.全概率公式与贝叶斯公式的应用。 第二章 随机变量及其分布 【学习目标】 1.理解随机变量的定义,了解用随机变量表示随机事件; 2.了解分布函数的定义及其性质,会利用分布函数计算事件的概率; 3.理解离散型随机变量及其分布列的定义、性质,掌握离散型随机变量的分布律 及分布函数; 4.掌握常见的离散型随机变量的分布的概率分布:两点分布、二项分布、泊松分 布; 5.理解连续型随机变量及概率密度的定义、性质掌握用密度函数计算概率,掌握 常见的连续型随机变量概率计算:均匀分布、指数分布和正态分布; 6.了解随机变量函数的概念,了解随机变量的简单函数的分布的求法。 【学习内容】 1.随机变量;

2离散型随机变量及其概率分布: 3.随机变量的分布函数: 4.连续型随机变量及其概率密度: 5.随机变量函数的分布。 【学习重点】 1随机变量、分布律、密度函数和分布函数的概念: 2.二项分布、均匀分布的概念和性质。 【学习难点】 1二项分布的推导及应用: 2.随机变量函数的概率分布。 第三章多维随机变量及其分布 【学习目标】 L.理解二维随机变量的概念: 2理解二维随机变量的边缘分布以及计算(离散、连续); 3.了解二维随机变量的条件分布,理解随机变量的独立性,掌握判断独立性的方 法。 【学习内容】 1二维随机交量及其分布; 2.条件分布与随机变量的独立性。 【学习重点】 1.由联合分布求概率: 2求边缘分布及条件分布的方法。 【学习难点】 1求离散型随机变量联合分布律的方法: 2.条件密度的导出: 3随机变量函数的分布。 第四章随机变量的数字特征 【学习目标】 1理解随机变量数字特征(数学期望、方差、标准差、协方差,相关系数)的概 A
——4—— 2.离散型随机变量及其概率分布; 3.随机变量的分布函数; 4.连续型随机变量及其概率密度; 5.随机变量函数的分布。 【学习重点】 1.随机变量、分布律、密度函数和分布函数的概念; 2.二项分布、均匀分布的概念和性质。 【学习难点】 1.二项分布的推导及应用; 2.随机变量函数的概率分布。 第三章 多维随机变量及其分布 【学习目标】 1.理解二维随机变量的概念; 2.理解二维随机变量的边缘分布以及计算(离散、连续); 3.了解二维随机变量的条件分布,理解随机变量的独立性,掌握判断独立性的方 法。 【学习内容】 1.二维随机变量及其分布; 2.条件分布与随机变量的独立性。 【学习重点】 1.由联合分布求概率; 2.求边缘分布及条件分布的方法。 【学习难点】 1.求离散型随机变量联合分布律的方法; 2.条件密度的导出; 3.随机变量函数的分布。 第四章 随机变量的数字特征 【学习目标】 1.理解随机变量数字特征(数学期望、方差、标准差、协方差,相关系数)的概

念。 2并会运用数字特征的基本性质计算具体分布的数字特征: 3掌握常用分布的数字特征的概念意义和实际背景,会根据随机变量的概率分布 求其函数的数学期望;会根据随机变量的联合概率分布求其函数的数学期望: 4.掌握随机变量独立性与相关系数的相互关系。 【学习内容】 1随机变量的数学期望与方差及其性质: 2随机变量函数的数学期望与方差: 3.随机变量的协方差与相关系数。 【学习重点】 1一维随机变量函数的数学期望和方差的计算及其性质: 2.二维随机变量的期望、方差、协方差、相关系数的计算,及独立性、相关性的 判断。 【学习难点】 随机变量函数的数学期望与方差。 第五章大数定律及中心极限定律 【学习目标】 1了解大数定律的概念;理解常见的大数定律的内容(如马尔可夫大数定律、切 比雪夫大数定律、贝努利大数定律、辛软大数定律); 2.了解中心极限定理的概念;掌握常见的中心极限定理(隶莫弗一拉普拉斯中心 极限定理、林德贝格一勒维中心极限定理)及其应用。 【学习内容】 1大数定律的概念: 2.中心极限定律的概念及应用。 【学习重点】 常见的大数定律与中心极限定理及其筒单应用。 【学习难点】 常见的中心极限定理及其应用。 第六章样本及抽样分布
——5—— 念。 2.并会运用数字特征的基本性质计算具体分布的数字特征; 3.掌握常用分布的数字特征的概念意义和实际背景,会根据随机变量的概率分布 求其函数的数学期望;会根据随机变量的联合概率分布求其函数的数学期望; 4.掌握随机变量独立性与相关系数的相互关系。 【学习内容】 1.随机变量的数学期望与方差及其性质; 2.随机变量函数的数学期望与方差; 3.随机变量的协方差与相关系数。 【学习重点】 1.一维随机变量函数的数学期望和方差的计算及其性质; 2.二维随机变量的期望、方差、协方差、相关系数的计算,及独立性、相关性的 判断。 【学习难点】 随机变量函数的数学期望与方差。 第五章 大数定律及中心极限定律 【学习目标】 1.了解大数定律的概念;理解常见的大数定律的内容(如马尔可夫大数定律、切 比雪夫大数定律、贝努利大数定律、辛钦大数定律); 2.了解中心极限定理的概念;掌握常见的中心极限定理(隶莫弗-拉普拉斯中心 极限定理、林德贝格-勒维中心极限定理)及其应用。 【学习内容】 1.大数定律的概念; 2.中心极限定律的概念及应用。 【学习重点】 常见的大数定律与中心极限定理及其简单应用。 【学习难点】 常见的中心极限定理及其应用。 第六章 样本及抽样分布