
试验设计与分析 响应面设计与分析 第六章 响应面试验设计与分析
试验设计与分析 响应面设计与分析

试验设计与分析 响应面设计与分析 1.什么是响应面法 >响应面设计方法(Response Surface Methodology,RSMW是利用合理的试验设 计方法并通过实验得到一定数据,采用多元二次回归方程来拟合因素与响应 值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变 量非线性问题及可视化的一种统计方法。 可分为: >中心复合试验设计(Central Composite Design,CCD); >Box-Behnken试验设计(BB)。 在响应分析中,观察值y可以表述为: y=f(x1,x2…,x1)+8 其中xx,是自变量,2…,的函数,是误差项。 在响应面分析中,首先要得到回归方程,然后通过对自变量x,x2, 的合理取值,求得使少=f(x,x2,…,x,)最优的值,这就是响应面设计 试验的目的
试验设计与分析 响应面设计与分析 Ø响应面设计方法(Response Surface Methodology,RSM)是利用合理的试验设 计方法并通过实验得到一定数据,采用多元二次回归方程来拟合因素与响应 值之间的函数关系,通过对回归方程的分析来寻求最优工艺参数,解决多变 量非线性问题及可视化的一种统计方法。 可分为: Ø中心复合试验设计(Central Composite Design,CCD); ØBox-Behnken试验设计(BB)。 在响应分析中,观察值y可以表述为: 其中 是自变量 的函数,ε是误差项。 在响应面分析中,首先要得到回归方程,然后通过对自变量 的合理取值,求得使 最优的值,这就是响应面设计 试验的目的。 ( , , , ) l y f x x x 1 2 f(x1,x2,,xl ) l x ,x ,,x 1 2 l x ,x ,,x 1 2 ( , , , )l y f x x x 1 2 ˆ
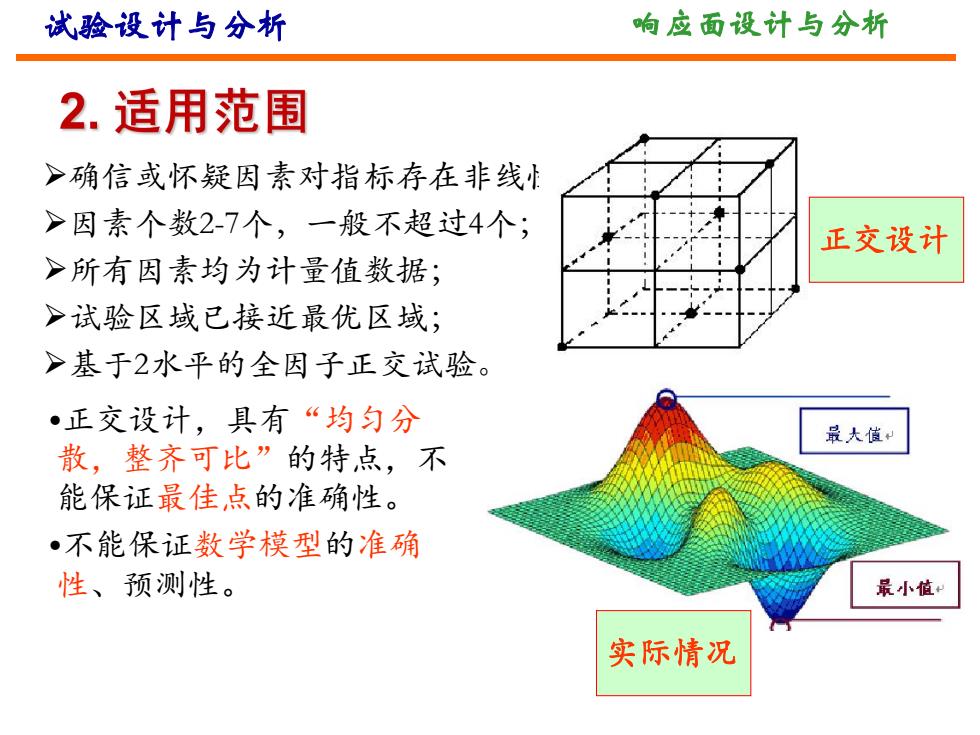
试验设计与分析 响应面设计与分析 2.适用范围 >确信或怀疑因素对指标存在非线 >因素个数2-7个,一般不超过4个; 正交设计 >所有因素均为计量值数据; >试验区域已接近最优区域; >基于2水平的全因子正交试验。 •正交设计,具有“均匀分 最大值 散,整齐可比”的特点,不 能保证最佳点的准确性。 •不能保证数学模型的准确 性、预测性。 最小值 实际情况
试验设计与分析 响应面设计与分析 Ø确信或怀疑因素对指标存在非线性影响; Ø因素个数2-7个,一般不超过4个; Ø所有因素均为计量值数据; Ø试验区域已接近最优区域; Ø基于2水平的全因子正交试验。 正交设计 实际情况 •正交设计,具有“均匀分 散,整齐可比”的特点,不 能保证最佳点的准确性。 •不能保证数学模型的准确 性、预测性

试验设计与分析 响应面设计与分析 3.一般步骤 1.确定因素及水平,注意水平数为2,因素数一 般不超过4个,因素均为计量值数据; 2.创建“中心复合”或“Box-Behnken”设计; 3.确定试验运行顺序(Display Design); 4.进行试验并收集数据; 5.分析试验数据; 6.优化因素的设置水平
试验设计与分析 响应面设计与分析 1. 确定因素及水平,注意水平数为2,因素数一 般不超过4个,因素均为计量值数据; 2. 创建“中心复合”或“Box-Behnken ”设计; 3. 确定试验运行顺序(Display Design); 4. 进行试验并收集数据; 5. 分析试验数据; 6. 优化因素的设置水平

试验设计与分析 响应面设计与分析 4.中心复合试验设计 ●中心复合设计(星点设计, 最大值 Central Composite Designs,CCD) 最小值 是应用得最为广泛的试验设计方法。 ●理解的关键CCD设计布点中心 中央点 点:点数要足够多,保证中央点 ·析因点 即最佳点的准确性。 ★轴点 析因点:构建多元回归模型,一个 立方体的2K顶,点,连续性。 图1CCD组成部分示意图 轴点:延展性,带有参数的2k个 轴向点,不需要准确性
试验设计与分析 响应面设计与分析 l中心复合设计(星点设计, Central Composite Designs,CCD) 是应用得最为广泛的试验设计方法。 l 理解的关键 CCD设计布点 中心 点:点数要足够多,保证中央点 即最佳点的准确性。 析因点:构建多元回归模型,一个 立方体的2 K顶点,连续性。 轴点:延展性,带有参数α的2k个 轴向点,不需要准确性