
试验设计与分析 试验结果分析 第四章试验结果的分析 方差分析
试验设计与分析 试验结果分析

试验设计与分析 试验结果分析 4.2试验结果的方差分析 1.方差分析的基本原理 Ronald Fisher 由英国统计学家R.A.Fisher首创, 为纪念Fisher以F命名,故方差 分析又称F检验(F test)。 用于推断多个总体均值有无差异。 方差分析法是将因素水平(或 交互作用)的变化所引起的试验结 果间的差异与误差波动所引起的试 验结果间的差异区分开来的一种数 学方法
试验设计与分析 试验结果分析 1. 方差分析的基本原理 由英国统计学家R.A.Fisher首创, 为纪念Fisher以F命名,故方差 分析又称 F 检验 (F test)。 用于推断多个总体均值有无差异。 方差分析法是将因素水平(或 交互作用)的变化所引起的试验结 果间的差异与误差波动所引起的试 验结果间的差异区分开来的一种数 学方法
试验设计与分析 试验结果分析 1、单因素方差分析原理 单因素方差分析是固定其它因素只考虑某一因素A对试验指 标的影响。为此将因素A以外的条件保持不变,取因素A的 个水平A1,A2,..,A,对水平Aj(i=1,2,.,r)重 复做n,次试验,得到试验指标的观察值列于下表。 单因素方差分析试验指标观察值。 水平 2 … Ale X11e X12e … Xin A2 X21 X22 …e X2n2 e e e … e Ar XHe 2 … Xm e e e … e Ar Xrle Xr2 …p Ym
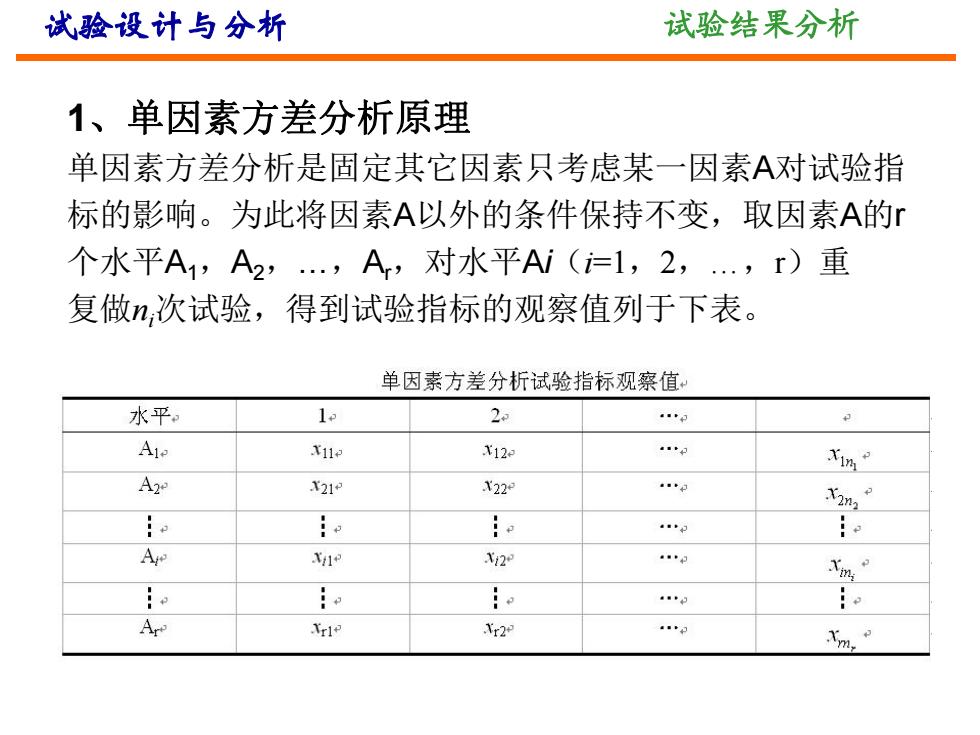
试验设计与分析 试验结果分析 1、单因素方差分析原理 单因素方差分析是固定其它因素只考虑某一因素A对试验指 标的影响。为此将因素A以外的条件保持不变,取因素A的r 个水平A1,A2,…,Ar,对水平Ai(i=1,2,…,r)重 复做ni次试验,得到试验指标的观察值列于下表

试验设计与分析 试验结果分析 我们假定在各个水平A:(1,2,…,x)下的样本为x,xa,…,X,它们来自具 有相同方差σ2,均值分别为4:的正态总体X:~N(4,02),其中4,σ2均为未知,并且 不同水平A:下的样本之间相互独立。 我们取下面的线性统计模型 x8=4:+8i eg~N(0,o23) 其中8为随机误差;=1,2,…,x;1,2,…,: 设 1 ∑n4 为总平均值,其中n=∑:
试验设计与分析 试验结果分析

试验设计与分析 试验结果分析 令 6:=4:-u 为第1个水平A的效应, ∑nd:=0,则有 x8=u+可:+88 e~N0,o2) 其中=1,2,…,x;≠1,2,…,no 方差分析的任务就是检验线性统计模型中x个总体N(以,σ2)中的各4:的相等性,即有 原假设品:1=42=…=4,, 对立假设A:4:4与至少有一对这样的,, 也就是下面的等价假设: A:61=63=…=6,=0 :6:≠0 至少有一个
试验设计与分析 试验结果分析