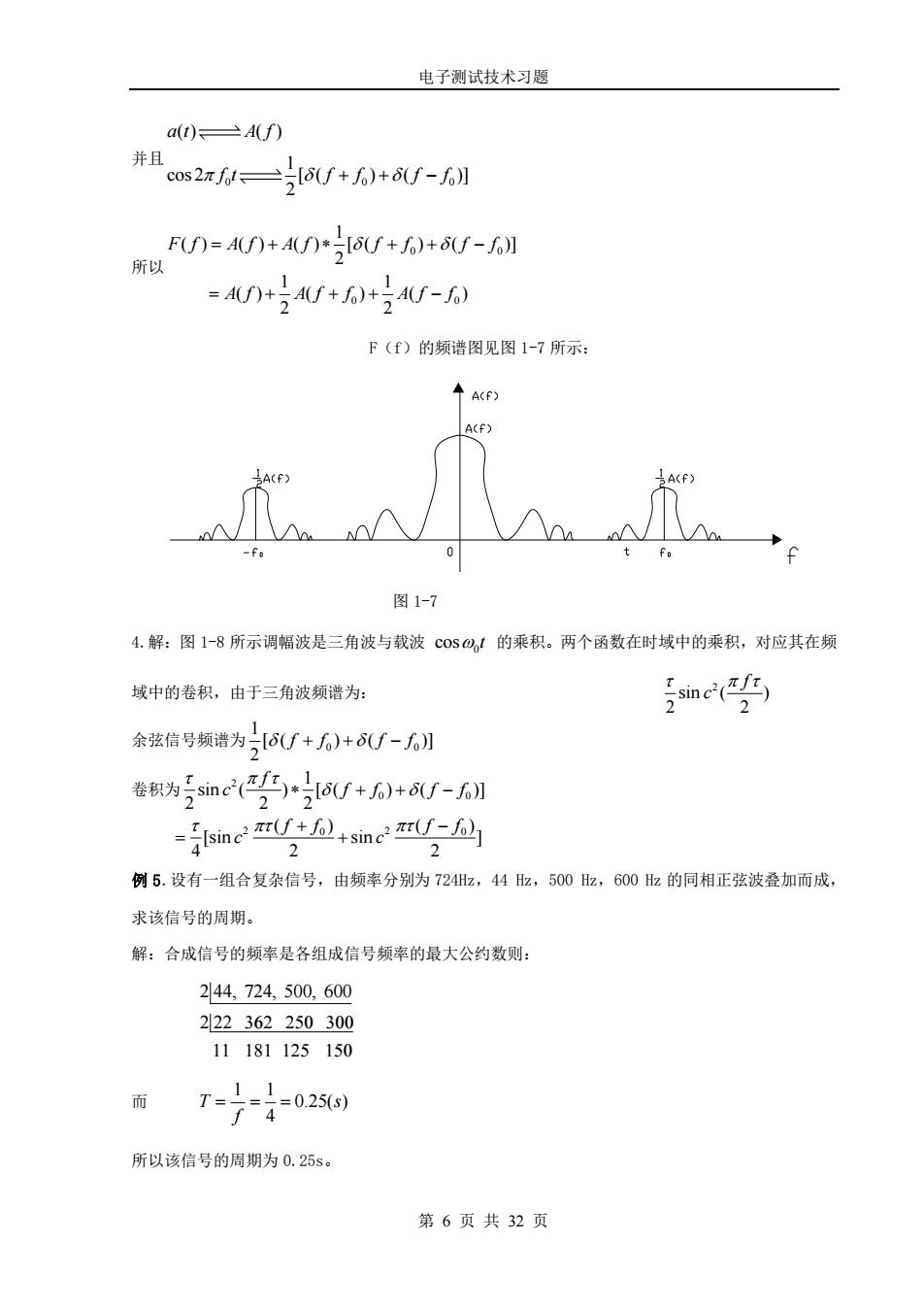
电子测试技术习题 a(t)A(f) 并 cos2ah=8U+)+8U-】 U)=A)+4)*6U+)+8f-6】 所以 =4+54U+60)+)4-0 F(f)的频谱图见图1-7所示: 图1-7 4.解:图1-8所示调幅波是三角波与载波c0s@,!的乘积。两个函数在时域中的乘积,对应其在频 域中的卷积,由于三角波频谱为: sine() 余弦信号频瑞为,6f+6)+6-6】 卷积为5c(要)6+6)+-6 in,sin 2 例5.设有一组合复杂信号,由频率分别为724细2,44z,500z,600z的同相正弦波叠加而成。 求该信号的周期。 解:合成信号的频率是各组成信号频率的最大公约数则: 244,724,500,600 222362250300 11181125150 而 1020 所以该信号的周期为0.25s。 第6页共32页
电子测试技术习题 第 6 页 共 32 页 并且 0 0 0 ( ) ( ) 1 cos 2 [ ( ) ( )] 2 a t A f f t f f f f + + − 所以 0 0 0 0 1 ( ) ( ) ( ) [ ( ) ( )] 2 1 1 ( ) ( ) ( ) 2 2 F f A f A f f f f f A f A f f A f f = + + + − = + + + − F(f)的频谱图见图 1-7 所示: 图 1-7 4.解:图 1-8 所示调幅波是三角波与载波 0 cos t 的乘积。两个函数在时域中的乘积,对应其在频 域中的卷积,由于三角波频谱为: 2 sin ( ) 2 2 f c 余弦信号频谱为 0 0 1 [ ( ) ( )] 2 f f f f + + − 卷积为 2 0 0 1 sin ( ) [ ( ) ( )] 2 2 2 f c f f f f + + − 2 2 0 0 ( ) ( ) [sin sin ] 4 2 2 f f f f c c + − = + 例 5.设有一组合复杂信号,由频率分别为 724Hz,44 Hz,500 Hz,600 Hz 的同相正弦波叠加而成, 求该信号的周期。 解:合成信号的频率是各组成信号频率的最大公约数则: 2 44, 724, 500, 600 2 22 而 1 1 0.25( ) 4 T s f = = = 所以该信号的周期为 0.25s

电子测试技术习题 例6.利用6函数的抽样性质,求下列表示式的函数值: (1) f)=e3- 解:6函数是一类应用广泛的重要函数。在卷积运算、傅立叶变换及测试系统分析中,利用它可以 简化许多重要结论的导出。本例题的目的在于熟悉并正确应用6函数的性质。 (1)由于f0)8)=fo)6)fu)=e-60=e6u) 则f)=e-8)=e'60 例8.已知e(t)和ht)的波形图如下图(a),()所示,试计算e()与h(t)的卷积积分。 e0)*0)=e(r)ht-rdr +e(t) 4h(t) 112d 1 (0) (b) 解:(I)反折:将()与h()的自变量t用t替换。然后将函数hMx)以纵坐标为轴线进行反折 得到与hx)对称的函数。见图(c)所示。 (2)平移:将函数(1-t)沿t轴正方向平移时间t,得函数1-t)。(注意,这里的t是参变 量),见图(d)所示。 (3)相乘并取积分:将(1一t)连续地沿t轴平移。对于不同的t的取值范围,确定积分上、下限, 并分段计算积分结果。 以下进行分段计算: a)当-<1一计,M!-)的他置知图回所示。追时0-)与没有重合部分.所型 e(t)*h)=0 )一号1<1时,的位置如图①所示,这时-与《)的圈形重区为至 把它作为卷积积分的上、下限,得: 第7页共32页
电子测试技术习题 第 7 页 共 32 页 例 6.利用 函数的抽样性质,求下列表示式的函数值: (1) 3 1 ( ) ( ); t f t e t − − = 解: 函数是一类应用广泛的重要函数。在卷积运算、傅立叶变换及测试系统分析中,利用它可以 简化许多重要结论的导出。本例题的目的在于熟悉并正确应用 函数的性质。 (1)由于 f t t f t ( ) ( ) ) = () • ( 3 1 1 ( ) ( ) ( ) t f t e t e t − − − = = 则 3 1 1 ( ) ( ) ( ) t f t e t e t − − − = = 例 8.已知 et() 和 ht() 的波形图如下图(a),(b)所示,试计算 et() 与 ht() 的卷积积分。 e t h t e h t d ( ) ( ) ( ) ( ) − = − 解:(1)反折:将 et() 与 ht() 的自变量 t 用τ替换。然后将函数 h( ) 以纵坐标为轴线进行反折, 得到与 h( ) 对称的函数 。见图(c)所示。 (2)平移:将函数 h t( ) − 沿τ轴正方向平移时间 t,得函数 h t( ) − 。(注意,这里的 t 是参变 量),见图(d)所示。 (3)相乘并取积分:将 h t( ) − 连续地沿τ轴平移。对于不同的 t 的取值范围,确定积分上、下限, 并分段计算积分结果。 以下进行分段计算: (a)当 1 2 − − t 时, h t( ) − 的位置如图(e)所示。这时 h t( ) − 与没有重合部分。所以 e t h t ( ) ( ) 0 = (b) 1 1 2 − t 时,的位置如图(f)所示。这时 h t( ) − 与 e( ) 的图形重叠区间为 1 2 − 至 t。 把它作为卷积积分的上、下限,得:

电子测试技术习题 40m0=0-0r-+6 (©)1<1<号时(即1>1,并且1-2<-弓时,则的位置如图(包)所示,这时的图形重叠区 间为(一宁山把它作为港积积分的上、下照:40r0-dr一子-君 (d)<1<3时,(即1-2>-同时1-2<1).由图可知积分区间为(t-2,1D.得 400=-h=-++是 (e)3<1<o时,h(t-t)与e(r)无重叠部分,见图(i)所示,这时 e()*h)=0 当-c1< 2 归纳以上结果得e(t)*h(t)= J313 416 当< 424 当1>3 卷积结果见图()所示。 hct-t 第8页共32页
电子测试技术习题 第 8 页 共 32 页 2 1 2 1 1 ( ) ( ) 1 ( ) 2 4 4 16 t t t e t h t t d − = − = + + (c) 3 1 2 t 时(即 t 1 ,并且 1 2 2 t − − 时),则的位置如图(g)所示,这时的图形重叠区 间为( 1 2 − ,1),把它作为卷积积分的上、下限,得: 1 2 1 3 3 ( ) ( ) 1 ( ) 2 4 16 t e t h t t d t − = − = − (d) 3 3 2 t 时,(即 1 2 2 t − − ,同时 t − 2 1 ),由图(h)可知积分区间为(t-2,1)。得 2 1 2 1 3 ( ) ( ) 1 ( ) t 2 4 2 4 t t e t h t t d − = − = − + + (e) 3 t 时, h t( ) − 与 e( ) 无重叠部分,见图(i)所示,这时 e t h t ( ) ( ) 0 = 归纳以上结果得 2 2 1 0 2 1 1 1 4 4 16 2 3 3 3 ( ) ( ) 1 4 16 2 3 3 4 2 4 2 0 t t t t t e t h t t t t t t − − + + − = − − + + 当 当 当 当 当 卷积结果见图(j)所示
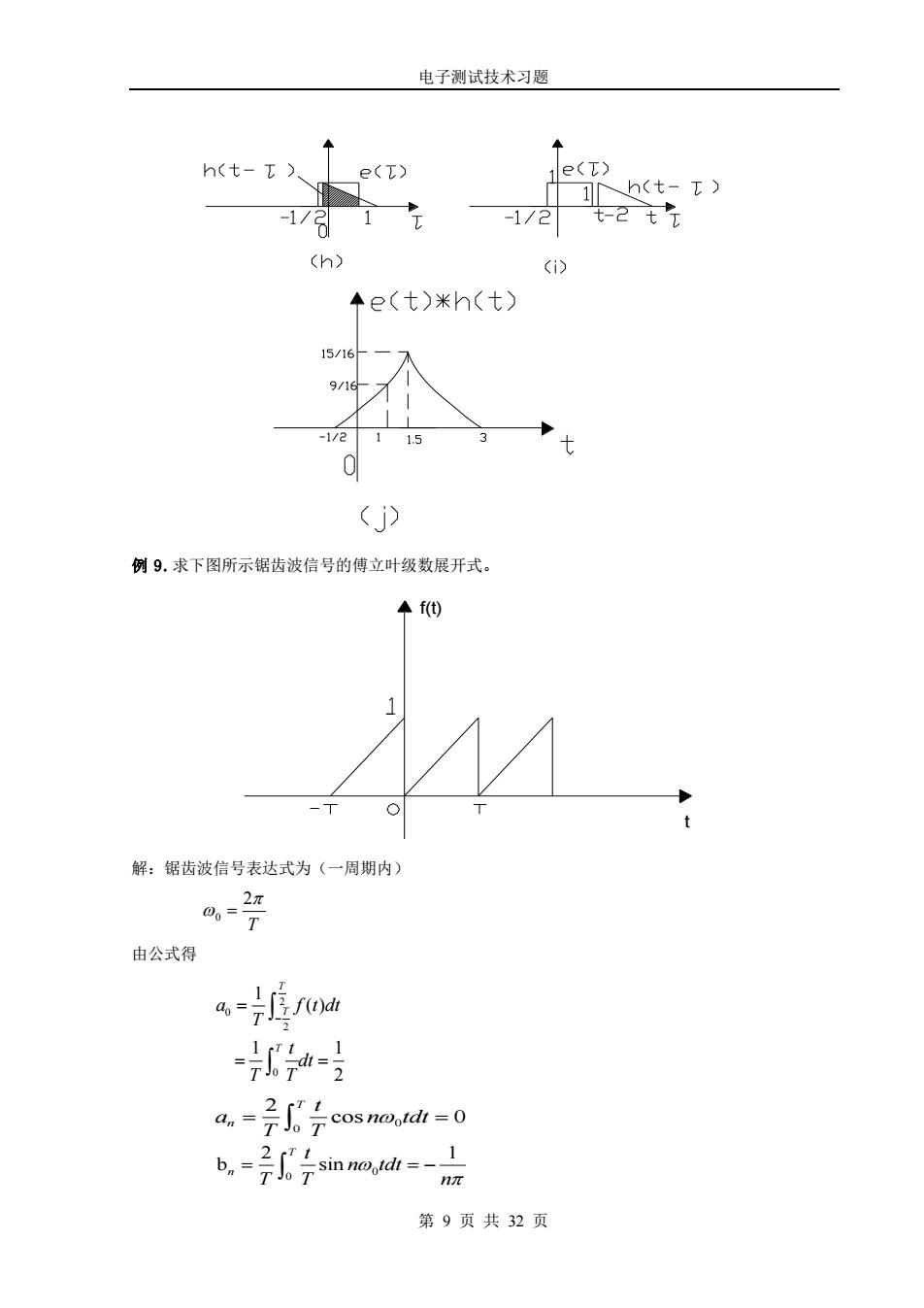
电子测试技术习题 h(t-t ) e(t) e() (t-t> -1/2 (h) +e(t)米h(t) 15/16 9/16 15 0 (j) 例9.求下图所示锯齿波信号的傅立叶级数展开式。 ◆f⑩ 解:锯齿波信号表达式为(一周期内) -27 由公式得 a=值oa a-子g7 o=0 。号mm= 第9页共32页
电子测试技术习题 第 9 页 共 32 页 例 9.求下图所示锯齿波信号的傅立叶级数展开式。 t f(t) 解:锯齿波信号表达式为(一周期内) 0 2 T = 由公式得 2 0 2 0 1 ( ) 1 1 2 T T T a f t dt T t dt T T − = = = 0 0 2 cos 0 T n t a n tdt T T = = 0 0 2 1 b sin T n t n tdt T T n = = −
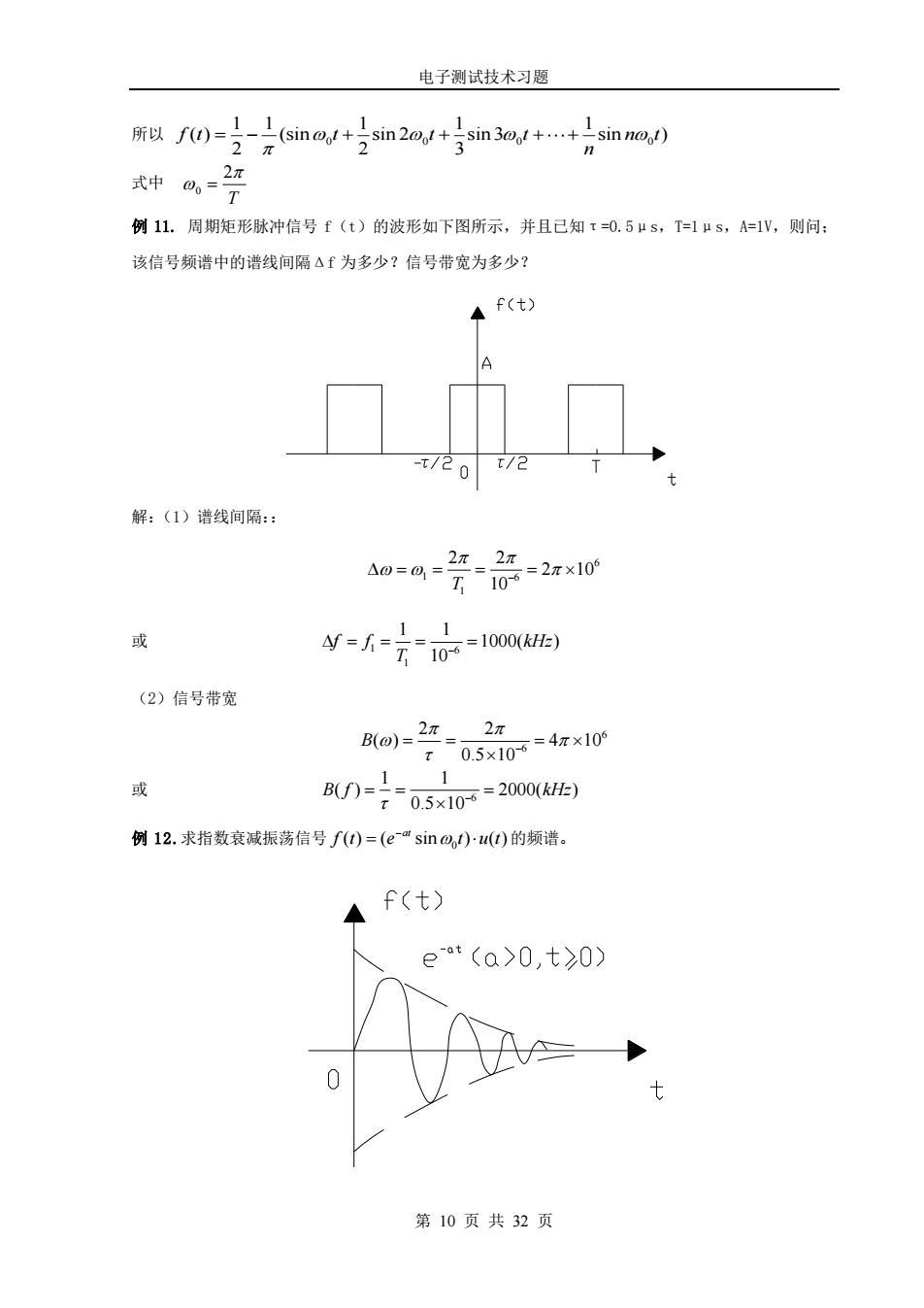
电子测试技术习题 所以0-号2ema时+号n2ay+写n3o+.+坊 inno) 例11.周期矩形脉冲信号f(t)的波形如下图所示,并且己知t=0.5μ5,T=1μs,A1V,则问 该信号缬谱中的谱线间隔△f为多少?信号带宽为多少? A f(t) t/col t/i 解:(1)谱线间隔: =-7-2ax0 或 y=人-7d=lw0u 1 (2)信号带宽 2π 或 8-o5i0=20na) 例12.求指数衰减振荡信号f=(esin,)u)的频谱。 A f(t) et (a>o,t>0) 第10页共32页
电子测试技术习题 第 10 页 共 32 页 所以 0 0 0 0 1 1 1 1 1 ( ) (sin sin 2 sin 3 sin ) 2 2 3 f t t t t n t n = − + + + + 式中 0 2 T = 例 11. 周期矩形脉冲信号 f(t)的波形如下图所示,并且已知τ=0.5μs,T=1μs,A=1V,则问; 该信号频谱中的谱线间隔Δf 为多少?信号带宽为多少? 解:(1)谱线间隔:: 6 1 6 1 2 2 2 10 T 10 − = = = = 或 1 6 1 1 1 1000( ) 10 f f kHz T − = = = = (2)信号带宽 6 6 2 2 ( ) 4 10 0.5 10 B − = = = 或 6 1 1 ( ) 2000( ) 0.5 10 B f kHz − = = = 例 12.求指数衰减振荡信号 0 ( ) ( sin ) ( ) at f t e t u t − = 的频谱