
上誉文通大¥ SHANGHAI JIAO TONG UNIVERSITY 4.2能控性的定义 状态方程 (t)=Ax+Bu 能控性: u(t)→x(t) 定义: 如果存在一个分段连续的输入能在有限时间间隔内,使 得系统从任意一个初始状态转移到任意的终止状态,则 称此系统是状态完全能控的,简称系统是能控的
4.2 能控性的定义 x &(t) = Ax + Bu 状态方程 能控性: 定义: 如果存在一个分段连续的输入能在有限时间间隔内,使 得系统从任意一个初始状态转移到任意的终止状态,则 称此系统是状态完全能控的,简称系统是能控的 u(t) → x(t)
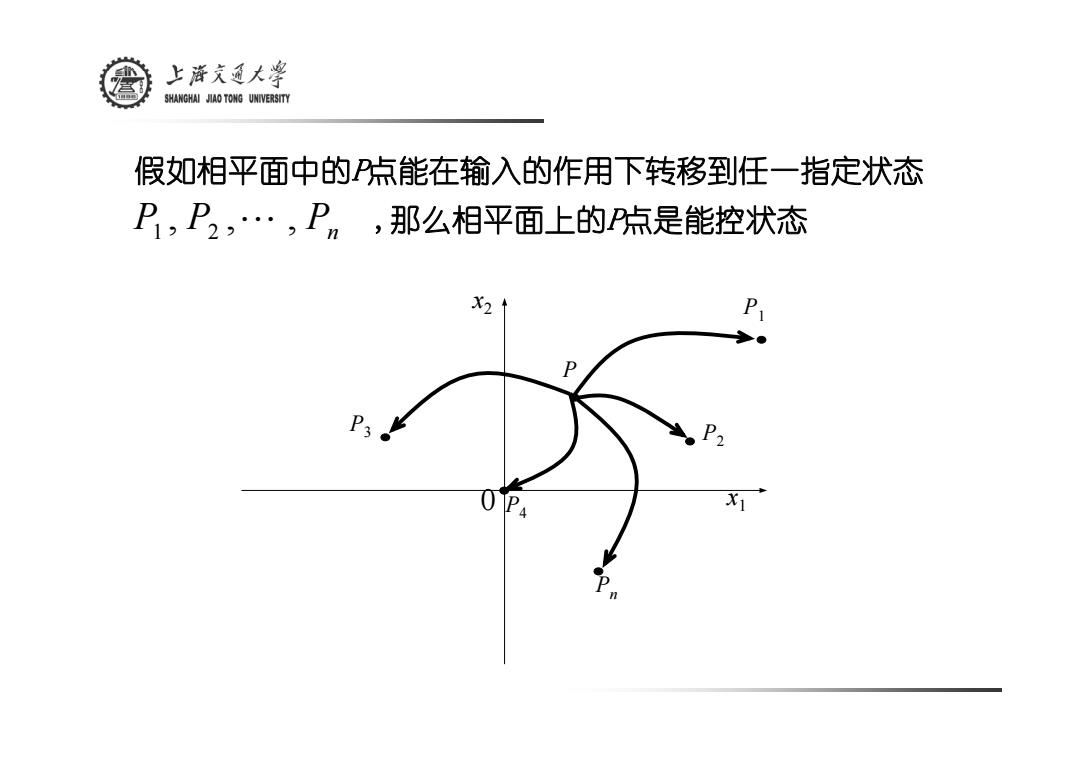
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 假如相平面中的点能在输入的作用下转移到任一指定状态 P,P2,…,P,,那么相平面上的P点是能控状态 P ● P D
假如相平面中的P点能在输入的作用下转移到任一指定状态 P1 2 ,,, P P L n ,那么相平面上的P点是能控状态 P P3 P1 P2 Pn P4 0 x1 x2
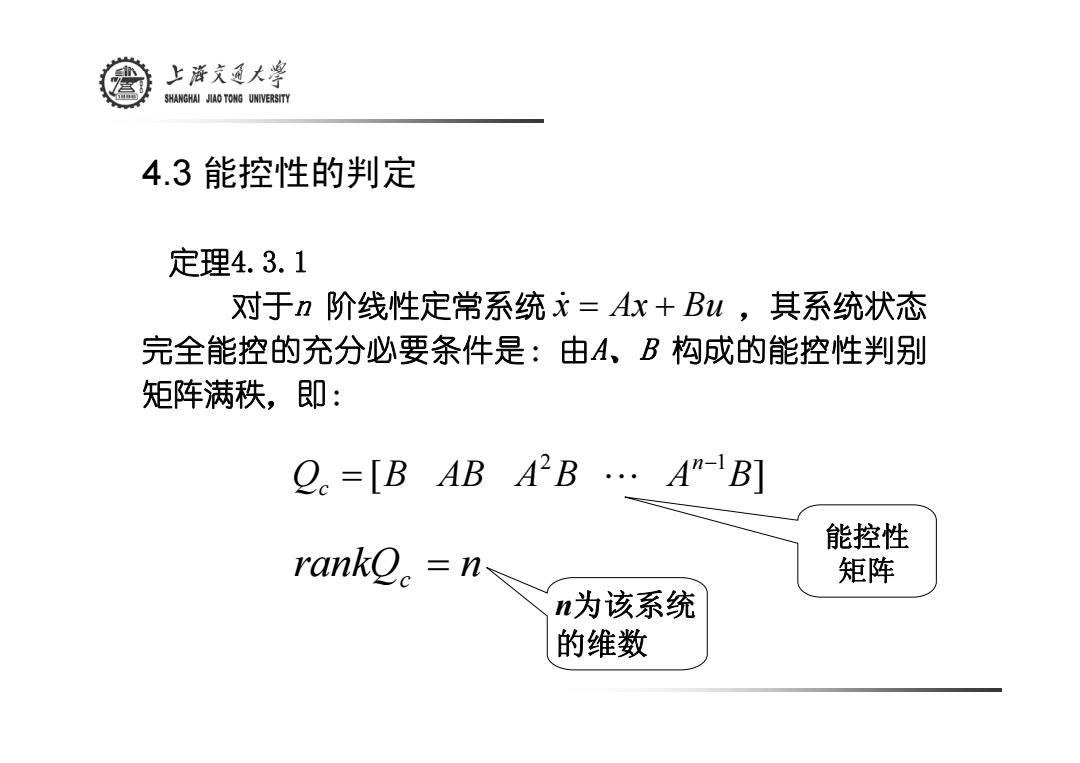
上游文通大¥ SHANGHAI JIAO TONG UNIVERSITY 4.3能控性的判定 定理4.3.1 对于n阶线性定常系统x=Ax+Bu,其系统状态 完全能控的充分必要条件是:由A、B构成的能控性判别 矩阵满秩,即: Q。=[B AB A2B·A-B] 能控性 rankO。=n 矩阵 n为该系统 的维数
定理4.3.1 对于n 阶线性定常系统 ,其系统状态 完全能控的充分必要条件是:由A、B 构成的能控性判别 矩阵满秩,即: x & = Ax + Bu [ ] 2 1 Q B AB A B A B n c − = L rankQc = n n为该系统 的维数 能控性 矩阵 4.3 能控性的判定