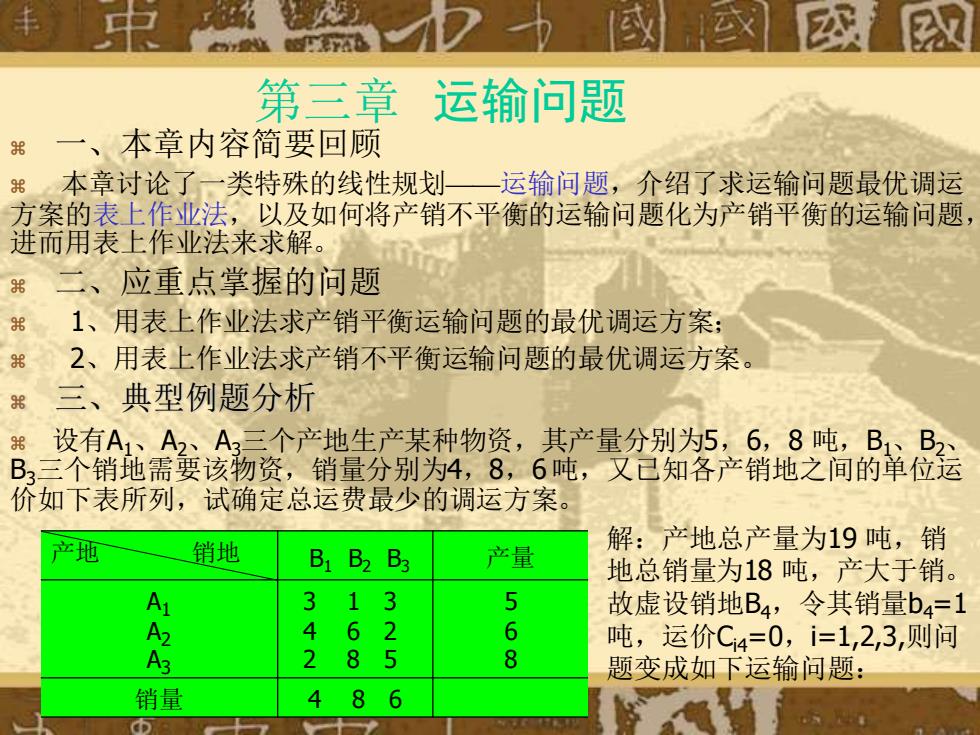
sTAb @或 级2双 第三章 运输问题 一、本章内容简要回顾 本章讨论了一类特殊的线性规划 一运输问题,介绍了求运输问题最优调运 方案的表上作业法,以及如何将产销不平衡的运输问题化为产销平衡的运输问题, 进而用表上作业法来求解。 二、应重点掌握的问题 1、用表上作业法求产销平衡运输问题的最优调运方案; 2、用表上作业法求产销不平衡运输问题的最优调运方案 96 三、典型例题分析 设有A1、A2A3三个产地生产某种物资,其产量分别为5,6,8吨,B1、B2 B3三个销地需要该物资,销量分别为4,8,6吨,又已知各产销地之间的单位运 价如下表所列,试确定总运费最少的调运方案。 产地 销地 解:产地总产量为19吨,销 B1 B2 B3 产量 地总销量为18吨,产大于销。 313 5 故虚设销地B4,令其销量b4=1 46 2 6 吨,运价C4=0,i=1,2,3,则问 3 2 85 8 题变成如下运输问题: 销量 4 86
第三章 运输问题 一、本章内容简要回顾 本章讨论了一类特殊的线性规划——运输问题,介绍了求运输问题最优调运 方案的表上作业法,以及如何将产销不平衡的运输问题化为产销平衡的运输问题, 进而用表上作业法来求解。 二、应重点掌握的问题 1、用表上作业法求产销平衡运输问题的最优调运方案; 2、用表上作业法求产销不平衡运输问题的最优调运方案。 三、典型例题分析 设有A1、A2、A3三个产地生产某种物资,其产量分别为5,6,8 吨,B1、B2、 B3三个销地需要该物资,销量分别为4,8,6 吨,又已知各产销地之间的单位运 价如下表所列,试确定总运费最少的调运方案。 产地 销地 B1 B2 B3 产量 A1 A2 A3 3 1 3 4 6 2 2 8 5 5 6 8 销量 4 8 6 解:产地总产量为19 吨,销 地总销量为18 吨,产大于销。 故虚设销地B4,令其销量b4=1 吨,运价Ci4=0,i=1,2,3,则问 题变成如下运输问题:

销地 B1 B2 B3 Ba 销地 量 B1 B2 B3 B4 u 产地 产地 3 1 3 0 5 A 8) 4(10 1 0 2 4 6 2 0 6 A2 0 (-4)6 (-9 9 2 8 5 0 8 A3 4 4(5) (-7 7 销量 4 8 6 Vj -5 1-7 0 (1) 用最小元素法得初始 (3)第一次调整量0=0, 调整 方案如下表所示: 后的方案如下表所示: 销地 销地 产地 BB2 B3 B4 产地 B1 B2B3 B4 量 量 4 1 1 A2 0 56 6 0 56 4 8 4 8 3 4 销量 4 8 6 销量 4 8 6 (2)用位势法计算检验数 (4)再用位势法计算检验数 如黄表所示: 如下页黄表所示:
销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 0 6 4 4 1 5 6 8 销量 4 8 6 1 (1)用最小元素法得初始 方案如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 0 6 4 4 1 0 9 7 vj -5 1 -7 0 (-7) (10) (-4) (-9) (8) (5) (3)第一次调整量θ=0,调整 后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 4 6 4 4 1 0 5 6 8 销量 4 8 6 1 (2) 用位势法计算检验数 如黄表所示: (4)再用位势法计算检验数 如下页黄表所示:
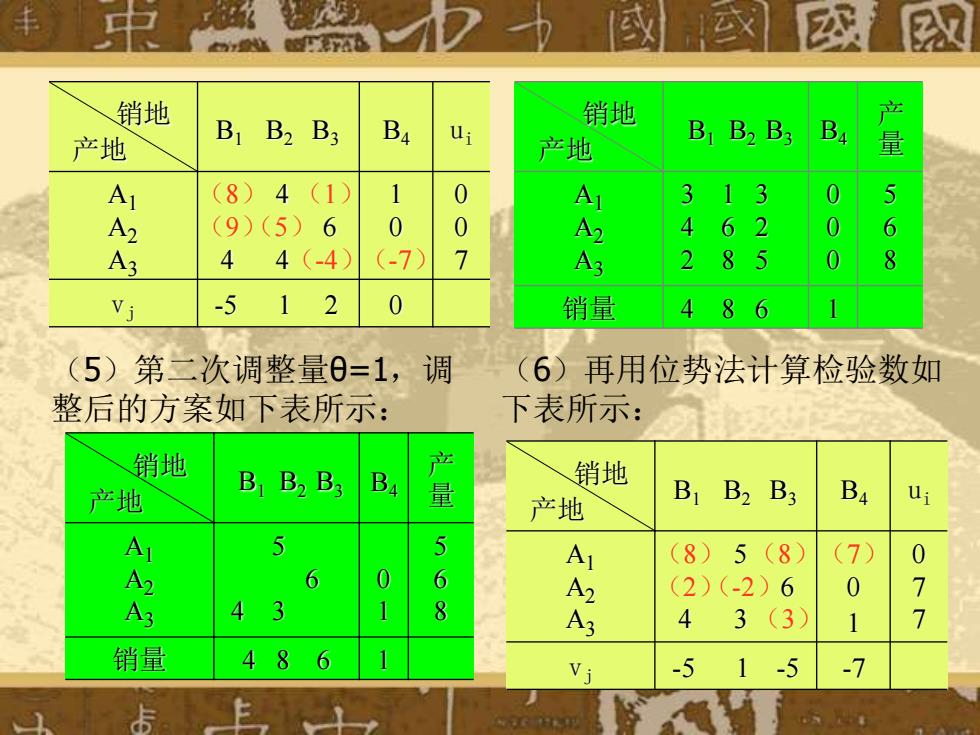
, rAB 销地 B B2 B3 B4 销地 产地 B B2 B 产地 量 A (8)4 (1》 1 0 Al 3 13 0 5 A (9)(5)6 0 0 4 6 0 6 A3 4 4(-4 (-7 7 A3 2 8 5 0 8 Vj -5 1 0 销量 4 8 6 (5)第二次调整量0=1,调 (6)再用位势法计算检验数如 整后的方案如下表所示: 下表所示: 销地 B B2 B: 产地 Ba 销地 量 产地 B1 B2 B3 B4 A 5 5 (8)5(8) (7 0 A A 6 0 6 A2 (2)(-2)6 0 77 A 4 3 1 8 A 4 3(3) 销量 4 86 1-5 -7
销地 产地 B1 B2 B3 B4 ui A1 A2 A3 4 6 4 4 1 0 0 0 7 vj -5 1 2 0 (-4)(-7) (9) (8) (5) (1) 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (5)第二次调整量θ=1,调 整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 6 4 3 0 1 5 6 8 销量 4 8 6 1 (6)再用位势法计算检验数如 下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 6 4 3 0 1 0 7 7 vj -5 1 -5 -7 (8) (8)(7) (2)(-2) (3)
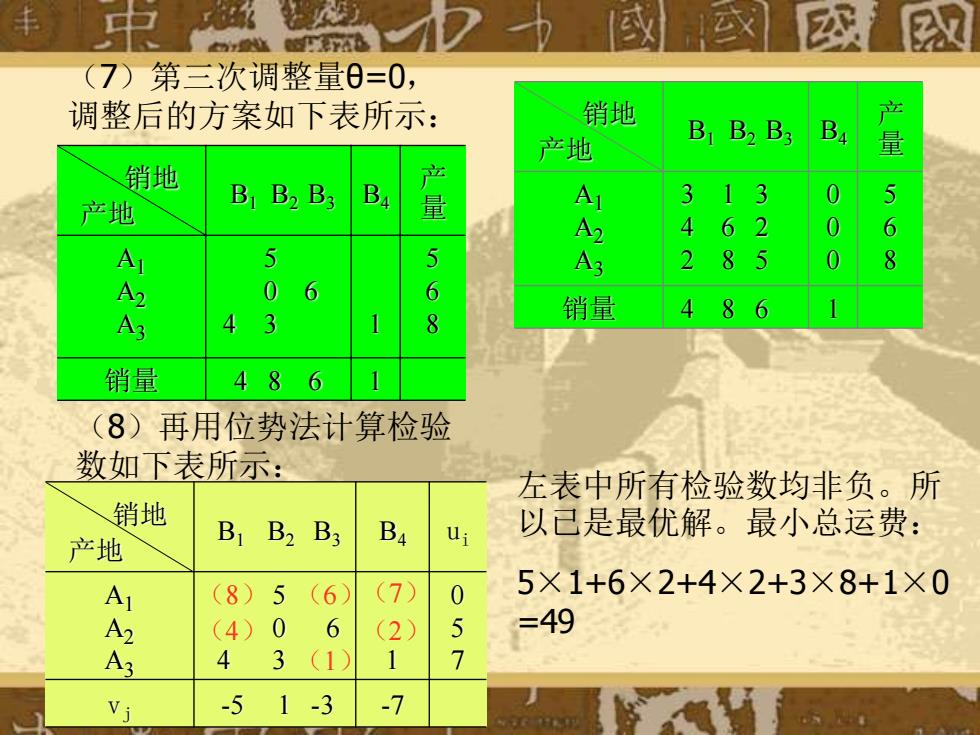
(7)第三次调整量0=0, 调整后的方案如下表所示: 销地 产地 BB2 B3 B4 量 销地 B B2 B3 B 产地 量 Al 3 13 0 5 4 6 2 0 6 5 43 2 8 0 8 A 0 6 6 3 8 销量 4 8 6 4 销量 4 8 6 (8)再用位势法计算检验 数如下表所示: 左表中所有检验数均非负。所 销地 产地 B B2 B3 Ba u 以己是最优解。最小总运费: A (8) 5 (6 (7) 0 5×1+6×2+4×2+3×8+1×0 A2 (4)0 6 (2 5 =49 4 3 (1) 1 7 Vj -5 1-3 -7
(7)第三次调整量θ=0, 调整后的方案如下表所示: 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 5 0 6 4 3 1 5 6 8 销量 4 8 6 1 销地 产地 B1 B2 B3 B4 产 量 A1 A2 A3 3 1 3 4 6 2 2 8 5 0 0 0 5 6 8 销量 4 8 6 1 (8)再用位势法计算检验 数如下表所示: 销地 产地 B1 B2 B3 B4 ui A1 A2 A3 5 0 6 4 3 1 0 5 7 vj -5 1 -3 -7 (8) (4) (6) (1) (7) (2) 左表中所有检验数均非负。所 以已是最优解。最小总运费: 5×1+6×2+4×2+3×8+1×0 =49

第四章 整数规划 、本章内容简要回顾 本章讨论了取整数解的特殊线性规划一整数规划间题。先介绍 了求解一般整数规划问题的分枝定界法;又介绍了求解纯整数规划 的割平面法;接着介绍了求解“01型整数规划”的隐枚举法。最后 较详细地讨论了“0-1型整数规划”的特例一指派问题的求解方法 (匈牙利法)。 二、应重点掌握的问题 8 1、求解“0-1型整数规划”的隐枚举法: 2、求解指派问题的匈牙利法。 三、典型例题分析
第四章 整数规划 一、本章内容简要回顾 本章讨论了取整数解的特殊线性规划—整数规划问题。先介绍 了求解一般整数规划问题的分枝定界法;又介绍了求解纯整数规划 的割平面法;接着介绍了求解“0-1型整数规划”的隐枚举法。最后 较详细地讨论了“0-1型整数规划”的特例—指派问题的求解方法 (匈牙利法)。 二、应重点掌握的问题 1、求解“0-1型整数规划”的隐枚举法; 2、求解指派问题的匈牙利法。 三、典型例题分析