s5多服务台排队系统模型(MM/C) MMC系统是指顾客按普阿松流输入,服务时间为 负指数分布,有C个服务台的单队多台并列服务系统。 它的结构见图10一7。在这种系统,顾客到达系统后排 成一个队列,然后到能给以服务的服务台接受服务,而 每个服务台的服务时间都服从相同参数的负指数分布, 服务完毕后顾客自动离去。 离去 服务台1 顾客到达 离去 服务台2 离去 图10一7 服务台C 由于顾客的到达间隔和服务时间都服从负指数分布,所以 这种系统象MMM系统一样,能直接利用生灭过程的计算 方法计算稳态概率。下面分别讨论MW/C模型的几种类型
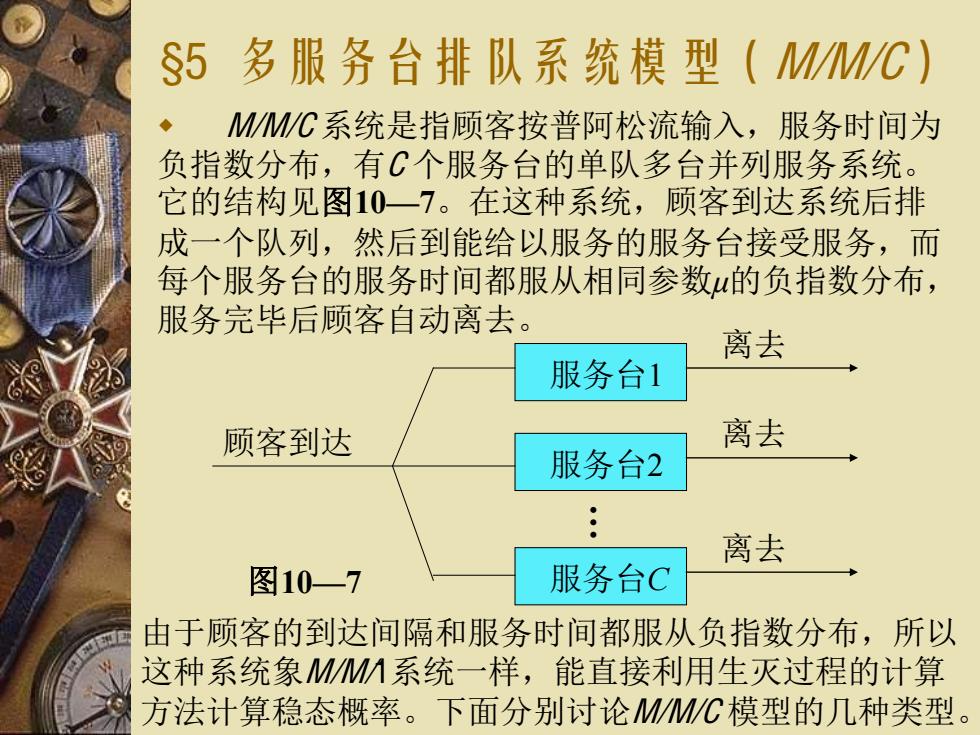
§5 多服务台排队系统模型(M/M/C) M/M/C 系统是指顾客按普阿松流输入,服务时间为 负指数分布,有C 个服务台的单队多台并列服务系统。 它的结构见图10—7。在这种系统,顾客到达系统后排 成一个队列,然后到能给以服务的服务台接受服务,而 每个服务台的服务时间都服从相同参数μ的负指数分布, 服务完毕后顾客自动离去。 服务台1 离去 服务台2 离去 服务台C 离去 … 顾客到达 由于顾客的到达间隔和服务时间都服从负指数分布,所以 这种系统象M/M/1系统一样,能直接利用生灭过程的计算 方法计算稳态概率。下面分别讨论M/M/C 模型的几种类型。 图10—7

5.1M/M/C/ool/oo模型 这是系统对顾客无限制,顾客源也无限制的多服务台 模型,其状态转移图如下: 2u 3u (C-1)w Cu Cu Cu 图10—8 入,=A n=0,1,2, nu 当n=1,2,,C-1 Un= lCu 当n2C 入-入-2…10 当m=2”c Cn nln-1“a aCn-c,当n≥C
5.1 M/M/C/∞/∞模型 这是系统对顾客无限制,顾客源也无限制的多服务台 模型,其状态转移图如下: 0 1 2 C-1 C C+1 λ λ λ λ λ λ λ μ 2μ 3μ (C-1)μ Cμ ● ● ● ● ● ● ● ● ● ● ● 图10—8 Cμ Cμ λn =λ n=0,1,2, … nμ 当n=1,2, …, C-1 Cμ 当n≥C μn = Cn = ( ) ( ) , n≥C C!C μ λ , n = 1,2, ,C 1. n! μ λ n - c n n 当 当 - = n n-1 1 n-1 n-2 0 μμ μ λλ λ

设p=WCu<1,(当2I时,系统无稳定状态) 则 P02 +交 入/ p当n=l2,c- n! Pn=CnPo= 当n≥C CIcn-co c+j CI BTPR C1-p2 Ls=Lg+Wu Ws-Ls/A W。=LgA=Ws-l/
设ρ=λ/Cμ<1,(当ρ≥1时,系统无稳定状态) 则 P0= ( ) ( ) 1 ρ 1 n! c! c c n n n μ λ μ c 1 λ n c n 0 1 n 0 1 C C 1 − + • = + − = = = − Pn= CnP0= ( ) P , n C n c C!C P , n 1,2, ,c 1 n! 0 0 n n μ λ μ λ − = − 当 当 Lq ( ) ( ) ( ) ( ) 2 j C!1 ρ ρ c ρ C! c ρ c C c C!C c j μ λ μ λ − = = − + = = = = = = + = 0 j 0 0 j 0 0 j 0 c j n c n P j P n-c P jP j P c Ls =Lq+λ/μ Ws =Ls /λ Wq =Lq /λ=Ws-1/μ

例4某公用电话亭有两台电话机,来打电话的人按普 阿松流到达,平均每小时24人,假定每次电话通话时间服 从负指数分布,平均为2分钟,求该系统各项指标。 解:p=/C=24÷2÷30=0.4 gglo8oao4a7 电话空闲的概率: 电话亭内有一个顾客的概率: P=(Wμ)P。=0.8X3/7=12/35 排队打电话的平均人数: La-V P 0 0.8×049605 1p)220-0.49 电话亭内打电话及等待的总平均人数: Ls=Lg+Wμ=16/105+0.8=20/21 每个顾客在电话亭内平均停留时间: W、=LsA=20/21÷24=5/126(小时)=50/21(分钟)
例4 某公用电话亭有两台电话机,来打电话的人按普 阿松流到达,平均每小时24人,假定每次电话通话时间服 从负指数分布,平均为2分钟,求该系统各项指标。 解:ρ=λ/Cμ=24÷2÷30=0.4 电话空闲的概率: ( ) ( ) 1 1 1 0.8 (0.8) /2(1 0.4) 3/7 2 1 ρ 1 c! c μ λ c 1 n 0 n! n μ λ = + + − = − + • − = P0= 电话亭内有一个顾客的概率: P1=(λ/μ)P0=0.8×3/7=12/35 排队打电话的平均人数: ( ) ( ) ( ) 16/105 21 0.4 7 3 0.8 0.4 1 ρ ρ C! c 2 2 2 μ λ = − = − = Lq P0 电话亭内打电话及等待的总平均人数: Ls=Lq+λ/μ=16/105+0.8=20/21 每个顾客在电话亭内平均停留时间: Ws =Ls /λ=20/21÷24=5/126(小时)=50/21(分钟)
每个顾客排队等候打电话的平均时间: W。=Lg小=16/105÷24=2/315(小时)=8/21(分钟) 来打电话的人需要等待的概率: P(W。>0)=1-PoP=1-3/7-12/35=8/35 MWM/C型系统与C个MM/1型系统的比较 现在就上面的例子加以说明,如果原问题中其它条件不变! 但顾客到达后在每台电话前各排一队,且进入队列后坚持不 变,这就形成了2个MM1系统,而每个队列的平均到达率为 入=2=12(人/小时)。计算这个MWMW1模型,并与上面的 MM/C模型比较,结果如下表所示: 指标 模型 M/M/1 M/M/2 从表上各 服务台空闲概率Po 3/5 3/7 指标对比 顾客必须等待的概率 12/35 8/35 可以看出, 平均队长Lg MWM/C模 28/105 16/105 型比C个 平均顾客数Ls 14/21 20/21 M/M/1模 平均逗留时间Wg 70/21分钟 50/21分钟 型有显著 平均等待时间Wg 28/21分钟 8/21分钟 优越性
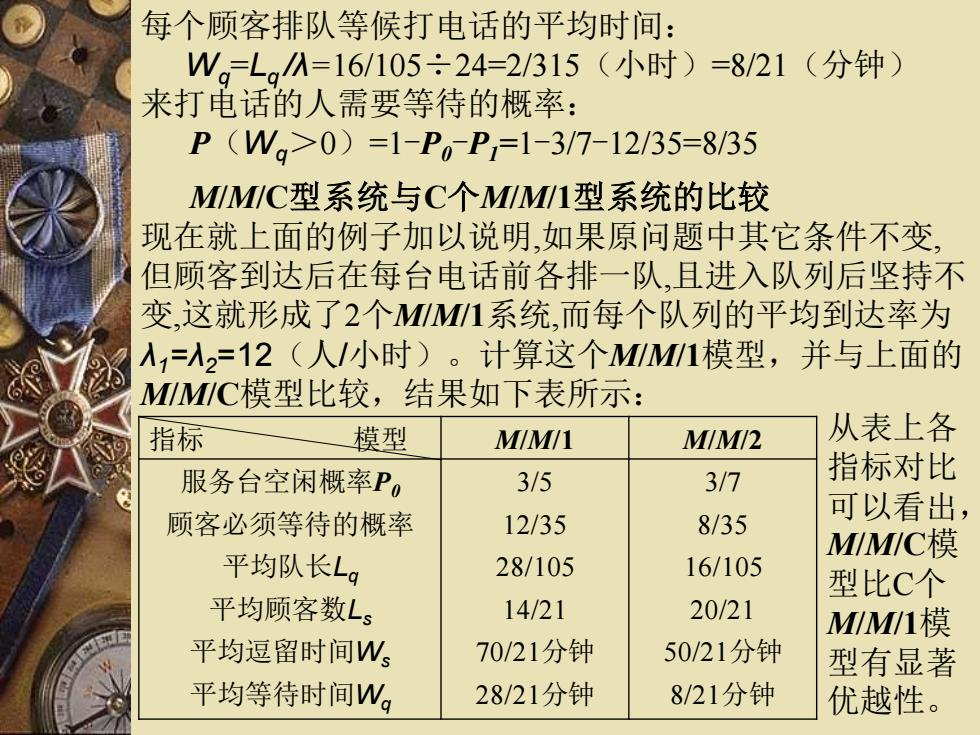
每个顾客排队等候打电话的平均时间: Wq =Lq /λ=16/105÷24=2/315(小时)=8/21(分钟) 来打电话的人需要等待的概率: P(Wq>0)=1-P0-P1=1-3/7-12/35=8/35 M/M/C型系统与C个M/M/1型系统的比较 现在就上面的例子加以说明,如果原问题中其它条件不变, 但顾客到达后在每台电话前各排一队,且进入队列后坚持不 变,这就形成了2个M/M/1系统,而每个队列的平均到达率为 λ1=λ2=12(人/小时)。计算这个M/M/1模型,并与上面的 M/M/C模型比较,结果如下表所示: 指标 模型 M/M/1 M/M/2 服务台空闲概率P0 3/5 3/7 顾客必须等待的概率 12/35 8/35 平均队长Lq 28/105 16/105 平均顾客数Ls 14/21 20/21 平均逗留时间Ws 70/21分钟 50/21分钟 平均等待时间Wq 28/21分钟 8/21分钟 从表上各 指标对比 可以看出, M/M/C模 型比C个 M/M/1模 型有显著 优越性