
§3最短路问题 在实践中常遇到的一类网络问题是最短路问题。给定一个有向 赋权图D=(V,A),对每一个弧a=(,),相应有权o≥0,指 定D中的v,为发点,v,为终点。最短路问题就是要在所有飞,到,的路 中,求出一条总权数最小的路。这里权数可以是距离,也可以是时 间,或者是费用等等。 最短路问题是最重要的优化问题之一,它不仅可以直接应用于 解决生产实际的许多问题,如管道铺设、线路安排、厂区布局、设 备更新等等,而且经常被作为一个基本工具,用于解决其它优化问 题
§3 最短路问题 在实践中常遇到的一类网络问题是最短路问题。给定一个有向 赋权图D=(V,A),对每一个弧a =(vi ,vj),相应有权ωij ≥0,指 定D中的vs 为发点,vt 为终点。最短路问题就是要在所有vs 到vt 的路 中,求出一条总权数最小的路。这里权数可以是距离,也可以是时 间,或者是费用等等。 最短路问题是最重要的优化问题之一,它不仅可以直接应用于 解决生产实际的许多问题,如管道铺设、线路安排、厂区布局、设 备更新等等,而且经常被作为一个基本工具,用于解决其它优化问 题

3.1狄克斯拉(Dijkstra)算法 最短路问题可以化为线性规划问题求解,也可以用动态规划方 法求解,这里介绍一种有效算法一狄克斯拉(Dijkstra)算法,这一 算法是1959年首次被提出来的。该算法适用于每条弧的权数o,≥0 情形。算法的基本思路:从发点,出发,有一个假想的流沿网络一 切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向 继续前进,则最先到达终点,的流所走过的路径一定是最短的。为 了实现这一想法,对假想流依次到达的点,依次给予标号,表示: 到这些点的最短距离。对于假想流尚未到达的点给予T标号,表示v 到这些点的最短距离的估计值。具体作法如下: s1°标p(v,)=0,其余点标T(v)=+o; $2°由刚刚获得标号的v,点出发,改善它的相邻点v,的T标号,即 新的T(o)=min{老的T(y),p()+o} 若T(y)=p()+@,则记k(y)=(前点标记); $3°找出具有最小T标号的点,将其标号改为p标号。若v,已获得p 标号,则已找到最短路,由k(,)反向追踪,就可找出v,到,的最 短路径,p()就是,到:的最短距离。否则,转2°
3.1 狄克斯拉(Dijkstra)算法 最短路问题可以化为线性规划问题求解,也可以用动态规划方 法求解,这里介绍一种有效算法—狄克斯拉(Dijkstra)算法,这一 算法是1959年首次被提出来的。该算法适用于每条弧的权数ωij ≥0 情形。算法的基本思路:从发点vs 出发,有一个假想的流沿网络一 切可能的方向等速前进,遇到新节点后,再继续沿一切可能的方向 继续前进,则最先到达终点vt 的流所走过的路径一定是最短的。为 了实现这一想法,对假想流依次到达的点,依次给予p标号,表示vs 到这些点的最短距离。对于假想流尚未到达的点给予T标号,表示vs 到这些点的最短距离的估计值。具体作法如下: 1°标p(vs)=0,其余点标T(vi)=+∞; 2°由刚刚获得p标号的vi 点出发,改善它的相邻点vj 的T标号,即 新的T(vj)=min{老的T(vj),p(vi)+ ωij } 若T(vj)= p(vi)+ ωij ,则记k(vj )=vi(前点标记); 3°找出具有最小T标号的点,将其标号改为p标号。若vt 已获得p 标号,则已找到最短路,由k(vt)反向追踪,就可找出vs 到vt 的最 短路径,p(vt)就是vs 到vt 的最短距离。否则,转2°
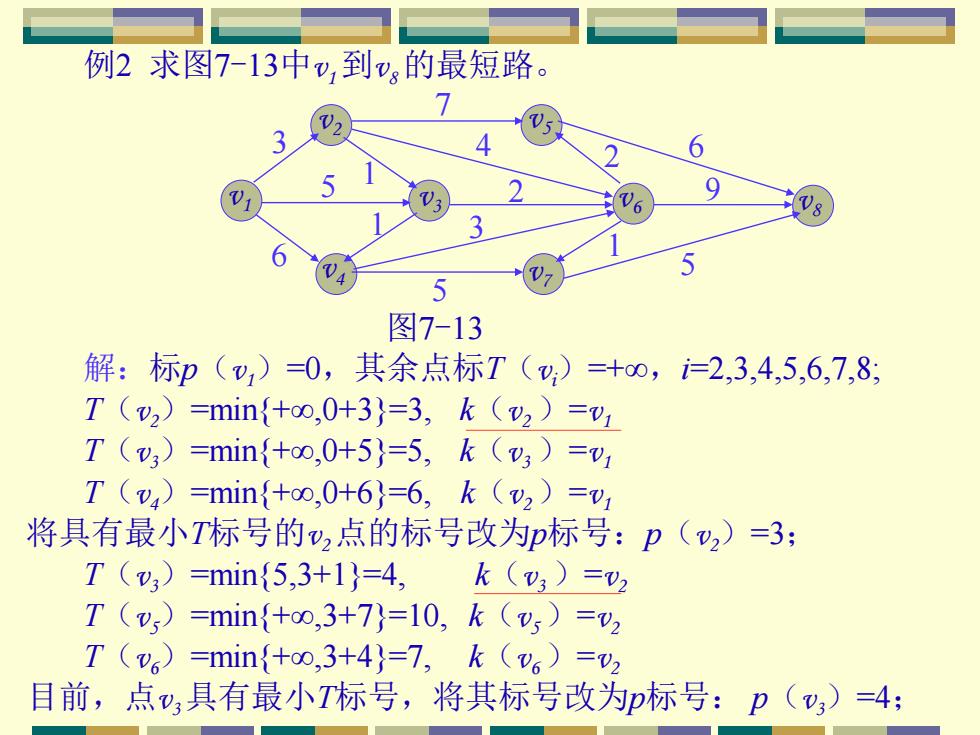
例2求图7-13中v,到v的最短路。 5 图7-13 解:标p()=0,其余点标T()=+oo,i2,3,4,5,6,7,8, T(v2)=min{+oo,0+3}=3,k(v2)=v T(v,)=min{+oo,0+5}=5,k(v,)=v1 T(v4)=min{+oo,0+6}=6,k(y2)=v1 将具有最小T标号的2点的标号改为p标号:p(2)=3: T(v,)=min{5,3+1}=4,k(v3)=v T(v5)=min{+oo,3+7}=10,k(v,)=v2 T(v6)=min{+oo,3+4}=7,k(v6)=v2 目前,点v,具有最小T标号,将其标号改为p标号:p(v)=4:
例2 求图7-13中v1 到v8 的最短路。 v4 v2 3 2 6 5 v3 v5 v6 v7 v8 6 3 5 5 2 1 1 1 4 7 9 解:标p(v1)=0,其余点标T(vi)=+∞,i=2,3,4,5,6,7,8; T(v2)=min{+∞,0+3}=3, k(v2 )=v1 T(v3)=min{+∞,0+5}=5, k(v3 )=v1 T(v4)=min{+∞,0+6}=6, k(v2 )=v1 将具有最小T标号的v2 点的标号改为p标号:p(v2)=3; T(v3)=min{5,3+1}=4, k(v3 )=v2 T(v5)=min{+∞,3+7}=10, k(v5 )=v2 T(v6)=min{+∞,3+4}=7, k(v6 )=v2 目前,点v3 具有最小T标号,将其标号改为p标号: p(v3)=4; v1 图7-13

p(,)=3 3大 p(,)=0 p(3)=4 6 5 5 T(v4)=min{6,4+1}=5,k(v4)=v; T(vs)=min{7,4+2}=6,k(6)=v 目前,点,具有最小T标号,将其标号改为p标号:p(v4)=5; T(6)=min{6,5+3}=6;T(v,)=min{+oo,5+5}=l0,k(,)=v4 目前,点,具有最小T标号,将其标号改为p标号:p()=6: T(v)=min{10,6+2}=8,k(v)=v6 T(v2)=min{10,6+1}=7,k(v2)=v6 T (vs)=min{+00,6+9)=15,k (vs)=v 目前,点v,具有最小T标号,将其标号改为p标号:p(,)=7: T(vg)=min{15,7+5}=l2,k(v)=v;p(vs)=8; T()=min{12,8+6}=12,p(g)=12;反向追踪找最短路径
v4 v2 3 2 6 5 v3 v5 v6 v7 v8 6 3 5 2 1 1 1 4 v 9 1 7 p(v1)=0 p(v2)=3 p(v3)=4 T(v4)=min{6,4+1}=5, k(v4 )=v3 T(v6)=min{7,4+2}=6, k(v6 )=v3 目前,点v4 具有最小T标号,将其标号改为p标号: p(v4)=5; T(v6)=min{6,5+3}=6; T(v7)=min{+∞,5+5}=10, k(v7 )=v4 目前,点v6 具有最小T标号,将其标号改为p标号: p(v6)=6; T(v5)=min{10,6+2}=8, k(v5 )=v6 T(v7)=min{10,6+1}=7, k(v7 )=v6 T(v8)=min{+∞,6+9}=15, k(v8)=v6 5 目前,点v7 具有最小T标号,将其标号改为p标号: p(v7)=7; T(v8)=min{15,7+5}=12, k(v8)=v7 ; p(v5)=8; T(v8)=min{12,8+6}=12, p(v8)=12;反向追踪找最短路径

最短路径为:V,→V2→V→6→→Vg: 因p(vg)=12,所以v→v的最短距离为12。 最短路问题不仅可以求解交通图中两点之间的最短距离,实际 中很多问题也可变为最短路问题加以求解。例如设备更新问题,厂 区合理布局问题等。兹举一例: 4例3(设备更新问题)某企业使用一台设备,在每年年底,企 业都要决策下年度是购买一台新设备呢?还是继续使用这台设备。 若购买新的,就要支付一笔购置费;如果使用旧设备,只要支付维 修费,而维修费随着设备的使用年限延长而增加。现根据以往统计 资料已经估算出设备在各年初的价格和不同使用年限的修理费用, 分别如表7-1、表7-2所示。 试确定一个五年内的设备更新计划,使五年内总支出最小。 3.2图上标示法 下面我们结合例3介绍求解最短路问题的图上标示法,它比狄克 斯拉算法更简洁
最短路径为:v1→v2→v3→v6→v7→v8 ; 因p(v8)=12,所以v1→v8 的最短距离为12。 最短路问题不仅可以求解交通图中两点之间的最短距离,实际 中很多问题也可变为最短路问题加以求解。例如设备更新问题,厂 区合理布局问题等。兹举一例: 例3(设备更新问题)某企业使用一台设备,在每年年底,企 业都要决策下年度是购买一台新设备呢?还是继续使用这台设备。 若购买新的,就要支付一笔购置费;如果使用旧设备,只要支付维 修费,而维修费随着设备的使用年限延长而增加。现根据以往统计 资料已经估算出设备在各年初的价格和不同使用年限的修理费用, 分别如表7-1、表7-2所示。 试确定一个五年内的设备更新计划,使五年内总支出最小。 3.2 图上标示法 下面我们结合例3介绍求解最短路问题的图上标示法,它比狄克 斯拉算法更简洁