
§4网络最大流问题 廿许多系统都包含了流量问题。例如公路系统中有车辆流,控制 系统有信息流,供水系统有水流等等。 现在考虑这样一个问题:某物资有m个生产基地A1,A2,.,Am 要通过铁路运到n个销地B1,B2,.,B,去。把铁路网上的车站看 作是顶点,两个车站间的铁路线看作是弧。可以认为在某条铁路线 上可运送的物资数量是有限的,我们把某条线路上的允许最大运送 量称为容量。这时要考虑如何安排运输方案,使得由产地运到销地 的物资总量达到最大。这就是在这个运输网中,求最大流问题。 4.1网络最大流概念 容量网络:在有向图D=(V,A),指定一个点为发点,记作 巴,指定另一个点为收点,记作,其余点叫作中间点。对于A的每 条弧(,y,),都对应一个权数C≥0,称为弧(,v)的容量,将这 样的赋权有向图叫作一个容量网经,记作D=(V,AC)
§4 网络最大流问题 许多系统都包含了流量问题。例如公路系统中有车辆流,控制 系统有信息流,供水系统有水流等等。 现在考虑这样一个问题:某物资有m个生产基地A1,A2,…,Am 要通过铁路运到n个销地B1,B2,…,Bn去。把铁路网上的车站看 作是顶点,两个车站间的铁路线看作是弧。可以认为在某条铁路线 上可运送的物资数量是有限的,我们把某条线路上的允许最大运送 量称为容量。这时要考虑如何安排运输方案,使得由产地运到销地 的物资总量达到最大。这就是在这个运输网中,求最大流问题。 4.1 网络最大流概念 容量网络:在有向图D=(V,A),指定一个点为发点,记作 vs ,指定另一个点为收点,记作vt ,其余点叫作中间点。对于A的每 条弧(vi ,vj),都对应一个权数cij ≥0,称为弧(vi ,vj)的容量,将这 样的赋权有向图叫作一个容量网络,记作D=(V,A,C)

如果在一个网络中,有多个发点或收点,则我们可以将其 变为只有一个发点和收点的网络。这只需增加一个新的总 发点和一个新的总收点。从总发点到各个发点分别连接 条容量为+∞的弧,从各个收点到总收点分别连接一条容量 为+∞的弧。这样就可将问题变为单发点和单收点的网络流 问题。所以,以后我们只讨论一个发点和一个收点的网络流问题。 在网络中,将通过弧(,?)的运量记作f,并称之为弧(,马) 上的流量。 可行流:对于容量网络D=(V,A,C),每条弧(,v)都给 定一个流量f,当f}满足下列条件时,称为可行流 1°容量限制:对每条弧(,y)∈A,有0≤fc 2°平衡条件:对于中间点v,∈V,流入量等于流出量,即 对于发点,和收点,则有,发出总量等于,收到总量,即 g∑f-∑=f) 称vf)为可行流f}的流量
如果在一个网络中,有多个发点或收点,则我们可以将其 变为只有一个发点和收点的网络。这只需增加一个新的总 发点和一个新的总收点。从总发点到各个发点分别连接一 条容量为+∞的弧,从各个收点到总收点分别连接一条容量 为+∞的弧。这样就可将问题变为单发点和单收点的网络流 问题。所以,以后我们只讨论一个发点和一个收点的网络流问题。 在网络中,将通过弧(vi ,vj)的运量记作f ij,并称之为弧(vi ,vj) 上的流量。 可行流:对于容量网络D=(V,A,C),每条弧(vi ,vj)都给 定一个流量 f ij ,当{f ij}满足下列条件时,称为可行流。 1°容量限制:对每条弧(vi ,vj)∈A,有0≤ f ij≤cij 2°平衡条件:对于中间点vi ∈V,流入量等于流出量,即 ∑f ji=∑f ij 对于发点vs 和收点vt ,则有vs 发出总量等于vt 收到总量,即 ∑f sj -∑f js= ∑f jt - ∑f tj =v(f ) 称v(f )为可行流{f ij}的流量。 j j j j j j
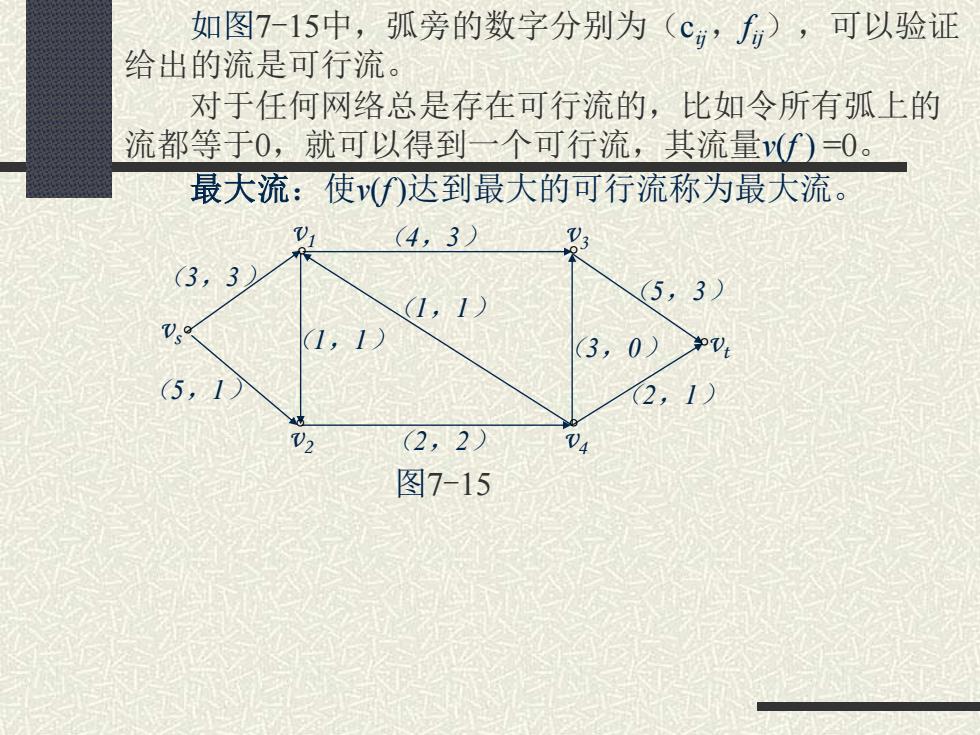
如图7-15中,弧旁的数字分别为(c,),可以验证 给出的流是可行流。 对于任何网络总是存在可行流的,比如令所有弧上的 流都等于0,就可以得到一个可行流,其流量y(f)=O。 最大流:使v()达到最大的可行流称为最大流。 (4,3) (3,3 1,1) 5,3) 1,1 (3,0)PV 2,1) (2,2) 图7-15
如图7-15中,弧旁的数字分别为(cij ,f ij),可以验证 给出的流是可行流。 对于任何网络总是存在可行流的,比如令所有弧上的 流都等于0,就可以得到一个可行流,其流量v(f ) =0。 最大流:使v(f )达到最大的可行流称为最大流。 ° ° ° ° ° ° vs vt v1 v2 v3 v4 (3,3) (4,3) (5,1) (1,1) (1,1) (5,3) (3,0) (2,1) (2,2) 图7-15

4.2计算最大流的标号法 这里介绍计算网络最大流的简便方法一标号法,此方法 是Ford一Fulkerson于1956年提出来的,它的原理是利用寻 找增广链来不断改善可行流。 设u是网络中v,到v,的一条链,规定,到v,的方向为u的方向。u 上与的方向一致的弧称为前向弧,前向弧的集合记为+,u上与4 的方向相反的弧称为后向弧,后向弧的集合记为。 (4,3) (3,3 (1,1) 5,3) 2。 (1,1) (3,0)V (5,1) 2,1) V2 (2,2) 04 图7-15 上图,链{2}上u+={(V,2),(v,V),(3 )} ={V1,V2
4.2 计算最大流的标号法 这里介绍计算网络最大流的简便方法—标号法,此方法 是Ford—Fulkerson 于1956年提出来的,它的原理是利用寻 找增广链来不断改善可行流。 设μ是网络中vs 到vt 的一条链,规定vs 到vt 的方向为μ的方向。 μ 上与μ的方向一致的弧称为前向弧,前向弧的集合记为μ+ ,μ上与μ 的方向相反的弧称为后向弧,后向弧的集合记为μ-。 ° ° ° ° ° ° vs vt v2 v4 (3,3) (4,3) (5,1) (1,1) (1,1) (5,3) (3,0) (2,1) (2,2) 图7-15 上图,链{vsv2v1v3vt}上 μ+={(vs,v2),(v1,v3), (v3, vt )} μ- ={v1,v2}。 v1 v3

若给一个可行流f},称网络中f=c的弧为饱和弧, 称f≤c,的弧为非饱和弧,称f=0的弧为零流弧,称f>0 的弧为非零流弧。 增广链:设(f)是可行流,u是v,到v,的一条链,若满足下 列条件,则称为关于f的增广链。(注意:f=f)}) 1°对于任何(,)∈+,0≤<c(前向弧为非饱和弧) 2°对于任何(,)∈,0<f≤c(后向弧为非零流弧) 如图7-15中,={v,v0}就是一条增广链。 定理:可行流是最大流,当且仅当不存在关于f的增广链。 证明:必要性:设f是最大流,若存在关于的增广链u,令 9=mm-fg到 则0>0,令 f0, (,y)∈u+ f*- f*-0, (v,∈0 ,y)∈u
若给一个可行流{f ij},称网络中 f ij =cij 的弧为饱和弧, 称 f ij< cij 的弧为非饱和弧,称f ij =0的弧为零流弧,称f ij>0 的弧为非零流弧。 增广链:设{f ij}是可行流,μ是vs 到vt 的一条链,若μ满足下 列条件,则称μ为关于 f 的增广链。(注意: f ={f ij}) 1°对于任何(vi ,vj)∈μ+ ,0≤ f ij < cij (前向弧为非饱和弧) 2°对于任何(vi ,vj)∈μ -,0 < f ij ≤ cij (后向弧为非零流弧) 如图7-15中,μ={vsv2v1v3vt}就是一条增广链。 定理:可行流 f﹡是最大流,当且仅当不存在关于 f﹡的增广链。 证明:必要性:设f﹡是最大流,若存在关于 f﹡的增广链μ,令 则θ >0,令 +θ, (vi ,vj)∈μ+ = -θ, (vi ,vj)∈μ - , (vi ,vj)∈μ = − + − ij vi v j μ ij ij vi v j μ θ min min c f , min f fij fij fij fij