
第6章 信息论基础 6.5信道模型和信道容量
第 6 章 信息论基础 6.5 信道模型和信道容量

信道容量和信道编码 回顾 M元调制产生的信号波形 ●用M=2k个信号波形,每个波形传递k比特信息。 ●M→oo时,只要≥-1.6dB ,可借助正交的信号波形使 差错概率任意小。 ●带宽W=Mf随k增加而指数增加。信道带宽利用率太低! 编码波形 (由二进制或非二进制序列产生的信号波形) ·W仅随k的增加而线性增加。更具有潜力获得较高带宽效率。 ·在功率受限系统(R/WK1)和带宽受限系统(R/W>1)中都 具有优越性能。 2
2 ⚫ W仅随 k 的增加而线性增加。更具有潜力获得较高带宽效率。 ⚫用 M=2k 个信号波形,每个波形传递 k 比特信息。 ⚫ ,可借助正交的信号波形使 差错概率任意小。 M dB → − 1.6 时,只要 b 回顾 ⚫带宽 W=Mf 随k 增加而指数增加。信道带宽利用率太低! 编码波形 (由二进制或非二进制序列产生的信号波形) ⚫在功率受限系统( R/W<1 )和带宽受限系统( R/W>1 )中都 具有优越性能。 M元调制产生的信号波形 信道容量和信道编码
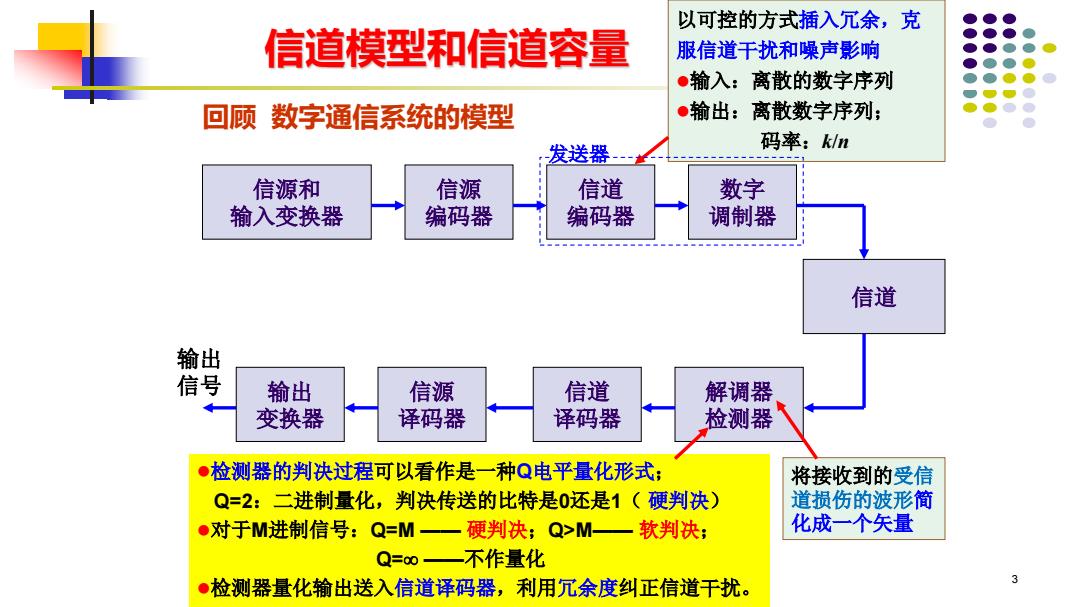
以可控的方式插入冗余,克 信道模型和信道容量 服信道干扰和噪声影响 ●输入:离散的数字序列 回顾数字通信系统的模型 ●输出:离散数字序列; 发送器 码率:kn 信源和 信源 信道 数字 输入变换器 编码器 编码器 调制器 信道 输出 信号 输出 信源 信道 解调器 变换器 译码器 译码器 检测器 ●检测器的判决过程可以看作是一种Q电平量化形式; 将接收到的受信 Q=2:二进制量化,判决传送的比特是0还是1(硬判决) 道损伤的波形简 ●对于M进制信号:Q=M—一硬判决;Q>M一软判决; 化成一个矢量 Q=0一不作量化 ●检测器量化输出送入信道译码器,利用冗余度纠正信道干扰。 3
3 信源和 输入变换器 信源 编码器 信道 信源 译码器 数字 调制器 信道 编码器 解调器 检测器 信道 译码器 输出 信号 输出 变换器 以可控的方式插入冗余,克 服信道干扰和噪声影响 ⚫输入:离散的数字序列 ⚫输出:离散数字序列; 码率:k/n 将接收到的受信 道损伤的波形简 化成一个矢量 ⚫检测器的判决过程可以看作是一种Q电平量化形式; Q=2:二进制量化,判决传送的比特是0还是1( 硬判决) ⚫对于M进制信号:Q=M —— 硬判决;Q>M—— 软判决; Q= ——不作量化 ⚫检测器量化输出送入信道译码器,利用冗余度纠正信道干扰。 回顾 数字通信系统的模型 信道模型和信道容量 发送器

6.5信道模型和信道容量 4
4 6.5 信道模型和信道容量

信道模型和信道容量 编码设计时常用的信道模型 可用以下三个参数来描述通信信道: ●信道的输入信号集(输入符号集)X ●信道的输出信号集(输出符号集)Y ●输入、输出序列(任意长度)关系的条件概率:P(,y2,Lynx,x2,Lxn) 如果对于所有: Pylx)=ΠPOy,Ix) i=l 则称信道是无记忆的。(i时刻的输出仅取决于i时刻的输入)
5 1 ( | ) ( | ) n i i i P y x P y x = = 编码设计时常用的信道模型 可用以下三个参数来描述通信信道: 信道模型和信道容量 1 2 1 2 ( , , | , , ) ⚫输入、输出序列(任意长度n)关系的条件概率 P y y y x x x L L n n : ⚫信道的输入信号集 (输入符号集)X ⚫信道的输出信号集 (输出符号集)Y 如果对于所有n: 则称信道是无记忆的。(i 时刻的输出仅取决于i 时刻的输入)