
Chapter 9 通过带限信道的数字通信 主要内容 ●带宽限制情况下线性调制信号v()=∑Ingt-nT)中 信号脉冲g()的设计 ●有ISI和AWGN信道的接收机设计 ●信道均衡
Chapter 9 通过带限信道的数字通信 主要内容 ⚫带宽限制情况下线性调制信号 中 信号脉冲g(t)的设计 ⚫有ISI和AWGN信道的接收机设计 ⚫信道均衡 ( ) n ( ) n v t I g t nT = −

9.1 带限信道的特征 2
2 9.1 带限信道的特征

带限信道的信号设计 带限信道的特征 ●信道的带宽被限制在指定的带宽WHz内 ●信道可以建模为一个线性滤波器,其等效低通频率响应为C(f) (等效低通冲激响应c()) 当f>W时,C(f)为0 发送信号: s(t)=Refv(t)e2) 等效低通接收信号:r()=v(r(-t)dπ+() 在频域,信号部分:R(f)=C(f)V(f) ●在信道带宽W内,频率响应C()可表示为: c(f)=c(f)eio) 定义:包络延迟 (f)=- 1 de(f) 2元 df 3
当 时,C( f )为0 3 带限信道的特征 ⚫信道的带宽被限制在指定的带宽 WHz 内 ⚫信道可以建模为一个线性滤波器,其等效低通频率响应为C( f ) (等效低通冲激响应c(t)) 带限信道的信号设计 r t v c t d z t ( ) ( ) ( ) ( ) − = − + ( ) ( ) 2 Re{ }c j f t s t v t e 发送信号: = 等效低通接收信号: ⚫在信道带宽W内,频率响应 C( f ) 可表示为: ( ) ( ) j ( f ) C f C f e = ( ) 1 ( ) 2 d f f df 定义:包络延迟 = −( ) ( ) ( ) 在频域,信号部分: R f C f V f s = f W
带限信道的信号设计 c(f)=c(f)eiou (f)=- 1 de(f) 2元 df 如果:对于所有f≤W: 幅度响应C(f) 为常数 信道是无失真 0(f)是频率的线性函数 或理想的 (x(f)为常数) C(f)儿不为常数 幅度失真 引起符号间 (f)不为常数 延时失真 串扰ISI 例: -37 ∠2r s74r六r0T七274757 (a)倍道输入 通过非理想信道后,接收信号的 发送的带限脉冲,周期零点:在士T,土2T等出现; 零交点不再是周期间隔的,连续 脉冲的序列将相互混叠,S 4 PAM脉冲序列:每一个的峰值安排在其他脉冲的周期零点上o简道输出
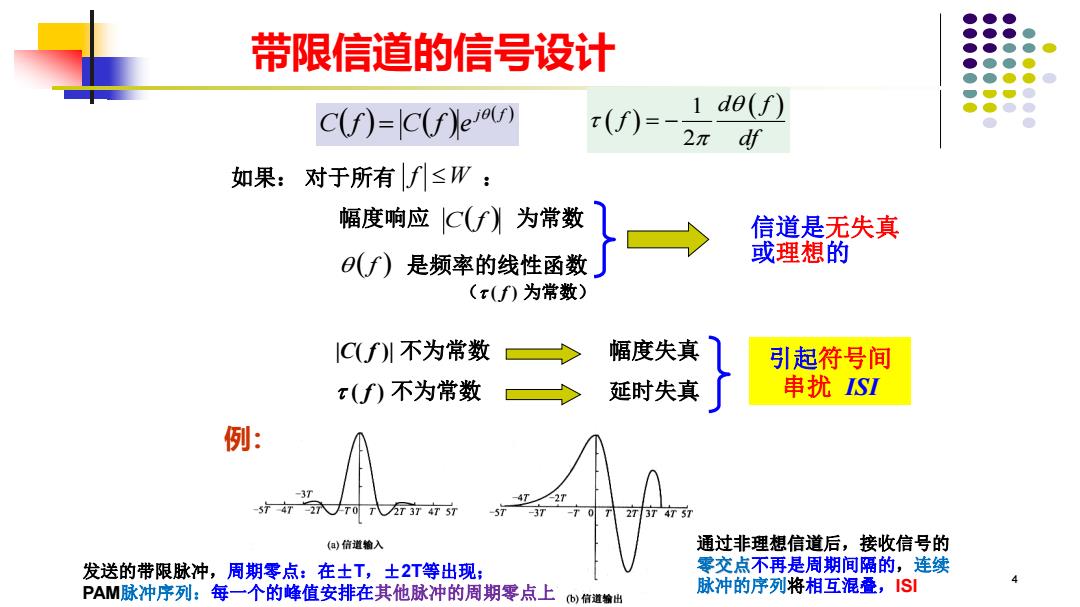
4 幅度响应 为常数 如果: 对于所有 : 是频率的线性函数 f W C(f ) ( f ) 信道是无失真 或理想的 |C( f )| 不为常数 ( f ) 不为常数 引起符号间 串扰 ISI ( ) ( ) j ( f ) C f C f e = ( ) 1 ( ) 2 d f f df = − 延时失真 幅度失真 带限信道的信号设计 ( ( f ) 为常数) 发送的带限脉冲,周期零点:在±T,±2T等出现; PAM脉冲序列:每一个的峰值安排在其他脉冲的周期零点上 通过非理想信道后,接收信号的 零交点不再是周期间隔的,连续 脉冲的序列将相互混叠,ISI 例:

带限信道的信号设计 除线性失真以外,信号通过信道传输时,还会遭受到其他损伤: ●非线性失真 ·频率偏移 ●相位抖动 ●脉冲噪声 ●热噪声 ·时变多径效应 本章只讨论带限信道的线性时不变滤波器的模型,为了数学处理方便, 只考虑它引入幅度和延迟失真,并加上高斯噪声。 5
5 除线性失真以外,信号通过信道传输时,还会遭受到其他损伤: ⚫ 非线性失真 ⚫ 频率偏移 ⚫ 相位抖动 ⚫ 脉冲噪声 ⚫ 热噪声 ⚫ 时变多径效应 ⚫ … … 本章只讨论带限信道的线性时不变滤波器的模型,为了数学处理方便, 只考虑它引入幅度和延迟失真,并加上高斯噪声。 带限信道的信号设计