
5.2.1最大似然载波相位估计 1
1 5.2.1 最大似然载波相位估计

信号参数估计 回顾: 如何获得似然函数,并导出参数估计值? (两条途径) N个标准正 ●由的展开式 交函数}根据r代)展开式随机变量[1,2,…r] 的联合PDF来导出; ●直接处理接收信号波形,从P(r8)的连续时间等效形式中导出. 接收信号: r(t)=s(t,θ)+n(t) 向量表示:r=[,,LLw】 r=s(e)+n n:零均值高 斯白噪声 r的联合PDF: P(r10)= (n-sn(0)月 exp 2o2 其中:n=丁J),(0)dh s(0)=s(t,(1)di To 指数项的自变量: m2a2-u=Jro)-k,o明rdh (用信号波形)和s(t,表示) σ2=N/2
2 如何获得似然函数 ,并导出参数估计值? (两条途径) 信号参数估计 ⚫由 r(t) 的展开式 根据r(t)展开式随机变量 [r1 , r2 , … rN ] 的联合PDF来导出; ⚫直接处理接收信号波形,从P(r | )的连续时间等效形式中导出. 0 ( ) ( , ) ( ) n n T s s t t dt = 0 ( ) ( ) n n T r r t t dt = 接收信号: 向量表示: 其中: ( ) n n r s n = + r t s t n t ( ) ( , ) ( ) = + n:零均值高 斯白噪声 2 2 1 1 ( ( )) ( | ) exp 2 2 N N n n n r s P r = − = − r的联合PDF: 指数项的自变量: 0 2 2 2 1 0 1 1 lim [ ( , )] [ ( ) ( , )] 2 N n n N n T r s t r t s t dt N → = − = − (用信号波形r(t)和s(t,)表示) 2 0 = N / 2 1 2 [ , , ] N r r r r = L L N个标准正 交函数{n (t)} 回顾:

信号参数估计 回顾: 定义:似然函数 A(0)=exp Pwora P(rB)关于信号参数0的最大化问题: P(r)最大 等价于 似然函数人(0) 最大 后面将根据A(B)最大的观点研究参数估计。 估计的参数为:O→{攻} 3
3 似然函数 0 2 0 1 ( ) exp [ ( ) ( , )] T r t s t dt N = − − P r( | ) 最大 似然函数 ( ) 最大 等价于 定义: 信号参数估计 P(r| ) 关于信号参数 的最大化问题: 后面将根据( )最大的观点研究参数估计。 估计的参数为: → { , } 回顾:

载波相位估计 最大似然载波相位估计 为简单起见,令(π=0),0→中 似然函数:)=ep-jrt0)-t,a No To N o To 不包含中 只有该项依 信号能量(对任何) 赖于的选择 -ce ML估计值u就是使A() o To 取最大的值 C是与无关的常数 对数似然函数: A,()= r0)s,d No To 略去常数项lnC 最大似然准则: A() 等价于、N() 最大 最大 4
4 r t s t dt N T L = 0 ( ) ( , ) 2 ( ) 0 对数似然函数: () () L 最大 最大 等价于 载波相位估计 最大似然载波相位估计 为简单起见,令 [ ( ) ( , )] ] 1 ( ) exp[ 2 0 0 r t s t dt N T = − − ( ) ( , ) ] 2 ( ) exp[ 0 0 r t s t dt N C T = 似然函数: = − + − s t dt N r t s t dt N r t dt N T0 T0 T0 ( , ) 1 ( ) ( , ) 2 ( ) 1 exp 2 0 0 2 0 ML估计值 就是使 取最大的 值 ML () ˆ 不包含 信号能量(对任何) 最大似然准则: ( 0), = → 只有该项依 赖于 的选择 C是与无关的常数 略去常数项lnC
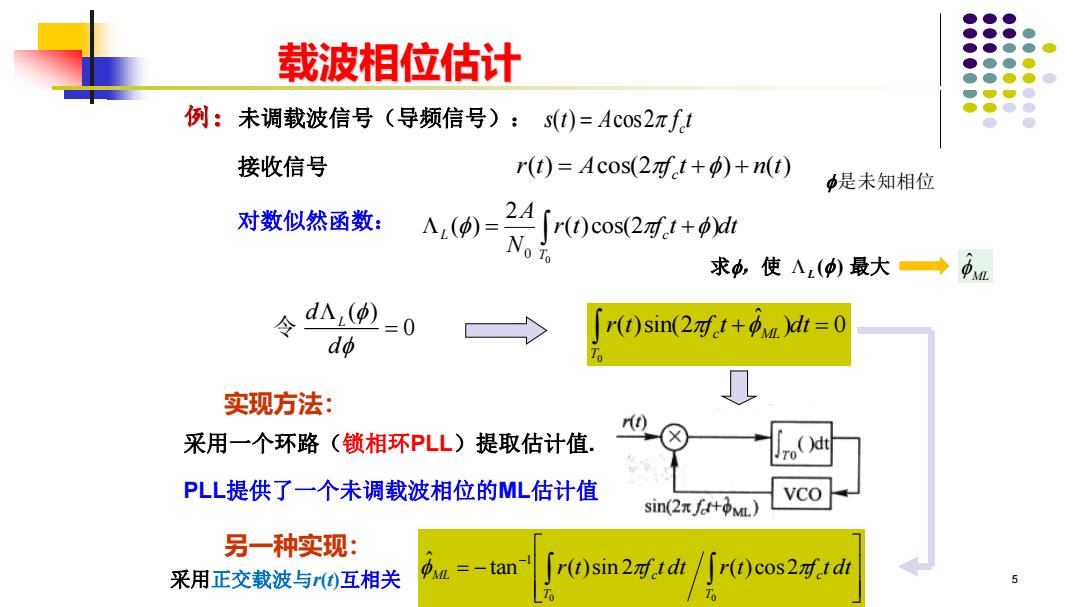
载波相位估计 例:未调载波信号(导频信号):s(t)=Acos2πft 接收信号 r(t)=Acos(2f+)+n(t) 中是未知相位 对数似然函数: A() 24∫r0cos(21+φ 求p,使Λ()最大→ dΛ(p) ≥0 r(t)sin(+)dt=0 do 实现方法: 采用一个环路(锁相环PLL)提取估计值. (dt PLL提供了一个未调载波相位的ML估计值 sin(2πJf什pa)) 另一种实现: 采用正交载波与()互相关 =-tan ∫r()sin2tdt/小r(0cos2对.tdh
5 ( ) cos2 = c 例:未调载波信号(导频信号): s t A f t 接收信号 采用一个环路(锁相环PLL)提取估计值. r(t) Acos(2 f t ) n(t) = c + + ( ) 0 L d d 令 = r t f t dt N A T L = c + 0 ( )cos(2 ) 2 ( ) 0 对数似然函数: ) 0 ˆ ( )sin(2 0 + = r t f t dt T c ML = − − r t f t dt r t f t dt T c T ML c 0 0 tan ( )sin 2 ( ) cos2 ˆ 1 另一种实现: 实现方法: 载波相位估计 PLL提供了一个未调载波相位的ML估计值 是未知相位 采用正交载波与r(t)互相关 求,使 L ( ) 最大 ML ˆ