信道模型和信道容量 四种信道模型 1.二进制对称信道BSC ·最简单的信道模型,应用于M=2,检测器采用硬判决的情况。 。把调制、解调、检测看成信道的一个部分一 合成信道 ●离散二进制输入X={0,1} ●离散二进制输出Y={0,1} 输入 信道 二进制 解调器 信道 和 信道 输出 数据 编码器 调制器 检测器 解码器 数据 合成的离散输入、离散输出信道 ●输入与输出之间关系:4个条件概率: PY=0|X=1)=P(Y=1|X=O)=p 输H P(Y=1X=1)=P(Y=01X=0)=1-p 每个输出比特仅与对应的一个输入比特有关一无记忆 6
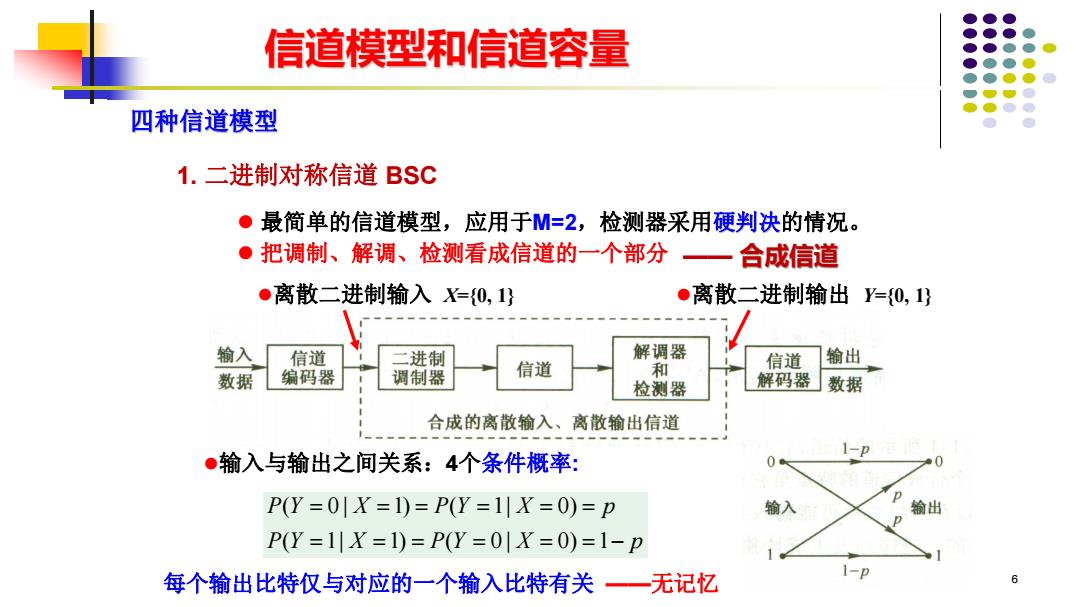
6 ⚫ 最简单的信道模型,应用于M=2,检测器采用硬判决的情况。 ⚫ 把调制、解调、检测看成信道的一个部分 ( 0 | 1) ( 1| 0) ( 1| 1) ( 0 | 0) 1 = = = = = = = = = = = = − P Y X P Y X p P Y X P Y X p 四种信道模型 1. 二进制对称信道 BSC —— 合成信道 ⚫输入与输出之间关系:4个条件概率: 信道模型和信道容量 ⚫离散二进制输入 X={0, 1} ⚫离散二进制输出 Y={0, 1} 每个输出比特仅与对应的一个输入比特有关 ——无记忆

信道模型和信道容量 2.离散无记忆信道DMC BSC推广一广义的离散输入、离散输出信道 图7-1-3离散g进制输人、Q进制输出信道 ●离散输入M元符号 ●Q电平离散输出 Q≥M=29 输入 信道 M元 解调器 信道 输出 和 数据 编码器 调制 信道 检测器 解码器」数据 检测器软判快 合成的离散输入、离散输出信道 ●合成信道的输入输出特性(信道和调制是无记忆时),用MQ个条件概率描述: P(Y=X=x)=P(ylx,) i=0,1,.2-1 j=0,1,.M-1 输入序列X、输出序列Y的联合概率: P(Y=V:Y =VL Y=VIX=u,X2 =4L X,=u)=IIP(Y =VIX=ug) 无记忆条件 k=l 条件概率P心U)可以表示成矩阵形式P=P,称为信道的转移概率矩阵
7 ( | ) ( | ) i j i j P Y = y X = x = P y x 2. 离散无记忆信道 DMC 输入序列X 、输出序列Y 的 联合概率: 1 1 2 2 1 1 2 2 1 ( , | , ) ( | ) = = = = = = = = = = n n n n n k k k k k P Y v Y v Y v X u X u X u P Y v X u L L i = 0, 1, … Q-1 j = 0, 1, … M-1 无记忆条件 条件概率P(yi |xj )可以表示成矩阵形式 P =[pij],称为信道的转移概率矩阵。 信道模型和信道容量 q ⚫离散输入M元符号 ⚫Q电平离散输出 Q M = 2 BSC推广——广义的离散输入、离散输出信道 ⚫合成信道的输入输出特性(信道和调制是无记忆时),用MQ个条件概率描述: 检测器软判决 M元 调制

信道模型和信道容量 3.离散输入、连续输出信道 调制器输入信号为离散字符,检测器的输出未经量化。 ·离散输入X ●连续输出Y 输入 信道 二进制 解调器 信道 输出 数据 编码器 调制器 信道 和 检测器 解码器 数据 合成的离散输入、离散输出信道 ●一组条件概率密度函数:P(y|X=x) x∈X,y∈R 例:AWGN信道: Y=X+N N:零均值,方差为σ2的高斯随机变量 P(y川X=x)= e-0-x212o2 √2πo ■对于任意给定的输入序列X,相应的输出序列y=X+N: i=1,2,..n 信道为无记忆的条件为: P(y,y2L yx,x2L x)=IP(y;lx,) 8 i=l
8 3. 离散输入、连续输出信道 调制器输入信号为离散字符,检测器的输出未经量化。 ⚫一组条件概率密度函数:P( y | X = x ) 例:AWGN信道: Y X N = + 2 2 1 ( ) / 2 ( | ) 2 − − = = y x P y X x e 1 2 1 2 1 ( , | , ) ( | ) = L L = n n n i i i 信道为无记忆的条件为: P y y y x x x P y x 信道模型和信道容量 ⚫离散输入 X ⚫连续输出Y N:零均值,方差为 2 的高斯随机变量 ◼对于任意给定的输入序列 Xi,相应的输出序列 Yi =Xi +Ni i=1,2,…n x X y R