新疆大学：《自动控制理论》课程教学课件（PPT讲稿）第五章 频率响应法

自动控制理论 4.二阶因子[1+25Tmj0+(joT)2]干1 1 1)G(jo)= o-20e+2g2 0 当%<1，略去20和 。项 L(o)≈-20lg1=0dB 低频渐近线 第五章频率响应法 2025/1/14

11 第五章 频率响应法 2025/1/14 4. 二阶因子 [1 2 ( ) ] 1 2 + Tn j + jTn  n n j G j       − + = 2 2 1 1 1) ( ) 2 2 2 ( ) 20lg (1 ) (2 ) n n L       = − − + 当 ,略去 和 2 项 2 1 2 n n n        L()  −20lg1= 0dB 自动控制理论 ——低频渐近线

自动控制理论 当0>1，略去1和25 n L(o)≈-200 =-401g -02 =0.3 On 0.5 -0.7 高频渐近线 -1.01 25o p(o)≈-arctan =0.1 1、 ⊙3 2 2-0.2 -0.3 >谐振峰值与谐振频率 -0.5 -0.7 1 6=1.0 G(j@)= 0.4 0.60.8 图5-13 5 第五章频率响应法 2025/1/14

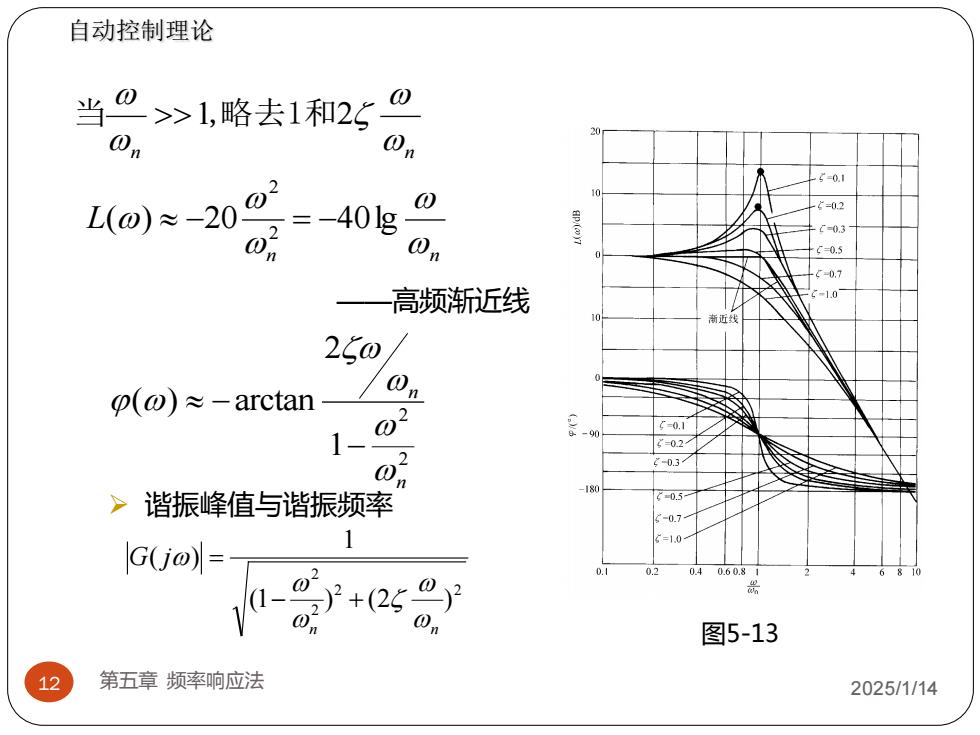
2 2 2 2 (1 ) (2 ) 1 ( ) n n G j       − + = 12 第五章 频率响应法 2025/1/14 n n     当 1,略去1和2 n n L     () 20 40lg 2 2  − = − 2 2 1 2 ( ) arctan n n       −  − 图5-13 自动控制理论 ➢ 谐振峰值与谐振频率 ——高频渐近线

自动控制理论 令g(o)=(1- 0+(25) 14 n 12 dg(o）=0 do 0=0,=0nV1-252 G(j@.)=M,=- 1 25V1-52 三6 0≤ξ≤0.707 0 0.20.40.60.8 1.0 图5-15 13 第五章频率响应法 2025/1/14

13 第五章 频率响应法 2025/1/14 2 2 2 2 ( ) (1 ) (2 ) n n g      令  = − + 0 ( ) =   d dg 2  = =n 1− 2 2 2 1 1 ( )    − G j r = Mr = 0    0.707 自动控制理论 图5-15

自动控制理论 5.滞后因子 e-yo -100 P( |G(j@)=e-9=1 -200 G(jo)=ejor +十++H p(0)=-t0 3)s G(jw)川=0dB -300 115 -400 -500 -600 .1 02 0.40.60.81 810 OT 图5-16 14 第五章频率响应法 2025/1/14

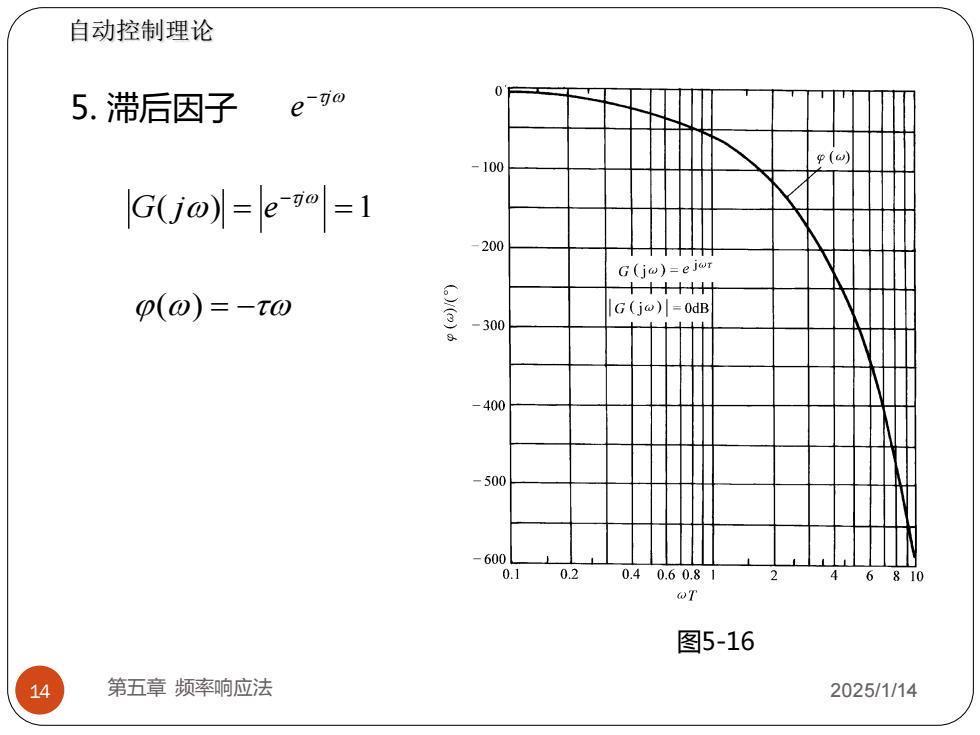
14 第五章 频率响应法 2025/1/14 图5-16 5. 滞后因子 j e − ( ) = =1 −   j G j e () = − 自动控制理论

自动控制理论 二、开环系统的伯德图 设开环传递函数 G(S)=G(S)G2(S).G(S) L(@)=201gG(j@)+201gG2(j@)+.+201gG,(j@) (@)=argG(jo)+argG2(jo)+.+argG,(jo) 例5-2 G(S)H(S)= 101+0.1S) 绘制Bode图。 S1+0.5S) 解(1)幅频特性 10+j0) G(j@)= jo(+j 15 第五章频率响应法 2025/1/14

15 第五章 频率响应法 2025/1/14 二、开环系统的伯德图 设开环传递函数 ( ) ( ) ( ) ( ) G S = G1 S G2 S Gn S ( ) 20lg ( ) 20lg ( ) 20lg ( ) L  = G1 j + G2 j ++ Gn j ( ) arg ( ) arg ( ) arg ( )   = G1 j + G2 j ++ Gn j 例5-2 (1 0.5 ) 10(1 0.1 ) ( ) ( ) S S S G S H S + + = 绘制Bode图。 解 ) 2 (1 ) 10 10(1 ( )     j j j G j + + = 自动控制理论 （1）幅频特性