新疆大学：《自动控制理论》课程教学课件（PPT讲稿）第五章 频率响应法

自动控制理论 二、由传递函数确定系统的频率响应 10(S+1) 10(S+1) 例5-1 G(S)= S2+4S+13 (S+2+3)(S+2-3) 试绘制系统的幅频和相频特性曲线。 解：令Sjg 10(2+1) G(U2)= (2+2+3)(2+2-j3) 10√5∠63.4° () +30 √29∠68.2°+√5∠-26.6° =1.857∠21.8° w/s-t 6 图5-6 6 第五章频率响应法 2025/1/14

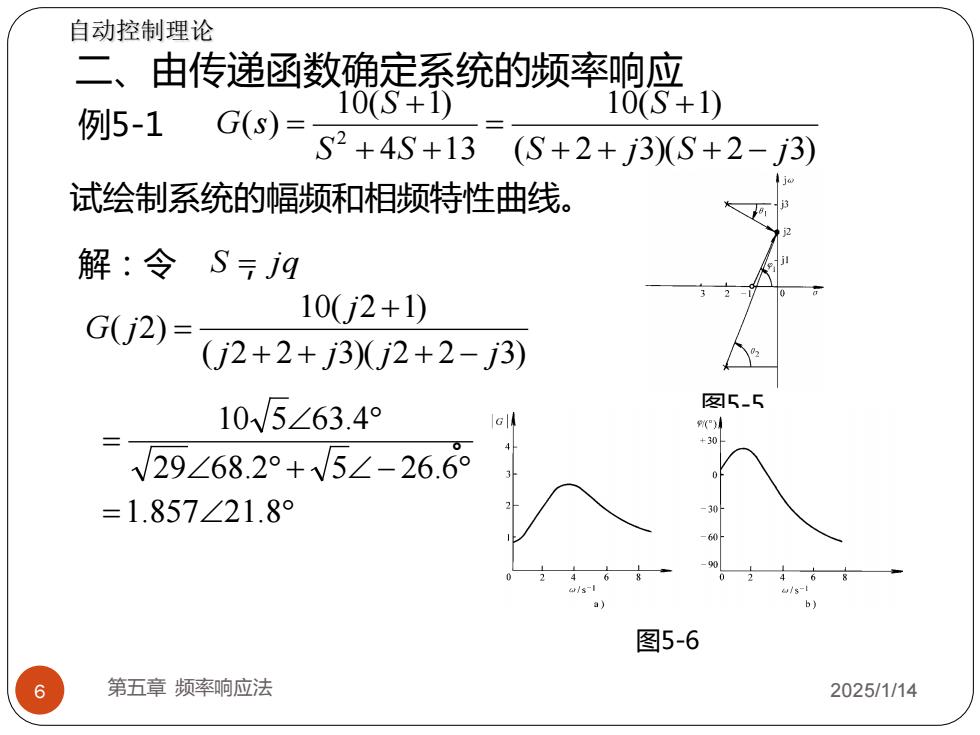
6 第五章 频率响应法 2025/1/14 二、由传递函数确定系统的频率响应 例5-1 ( 2 3)( 2 3) 10( 1) 4 13 10( 1) ( ) 2 S j S j S S S S G s + + + − + = + + + = 试绘制系统的幅频和相频特性曲线。 解：令 S ， = jq ( 2 2 3)( 2 2 3) 10( 2 1) ( 2) j j j j j G j + + + − + = 。 =     + −    = 1.857 21.8 29 68.2 5 26.6 10 5 63.4 自动控制理论 图5-5 图5-6

自动控制理论 第二节 对数坐标图 对数坐标图 20lgG(jo)/dB~∞ lp(0)/c~∞ 一、 典型因子的伯德图 L() 1.比例因子K 201gK=-2018K 20lg K 0dB 0.1 2.一阶因子(1+joT)干1 9()/()4 0 /s-1 (o)=-arctan 01 图5-7 ()=-20g1+ 1 01 ,01 第五章频率响应法 2025/1/14

第二节 对数坐标图 2 1 ( ) 20lg 1 ( )   L  = − + 第五章 频率响应法 2025/1/14 7 对数坐标图    2 0l g ( ) / ~ ( )/ ~ { G j d B c    1. 比例因子K K K 1 20lg = −20lg 图5-7 2. 一阶因子 (1+ jT) 1 1 ( ) arctan     = − 自动控制理论 一、典型因子的伯德图 T 1 ,1 =

自动控制理论 当o<w,时，略去(0)2，L(@)≈-20g1=0dB ⊙1 当o>0,时，略去1，L(0)≈-20lg 01 10 渐近线 转折频率 0 渐近线 -10 精确曲线 -20 -45 -90 0品7 图5-8 8 第五章频率响应法 2025/1/14

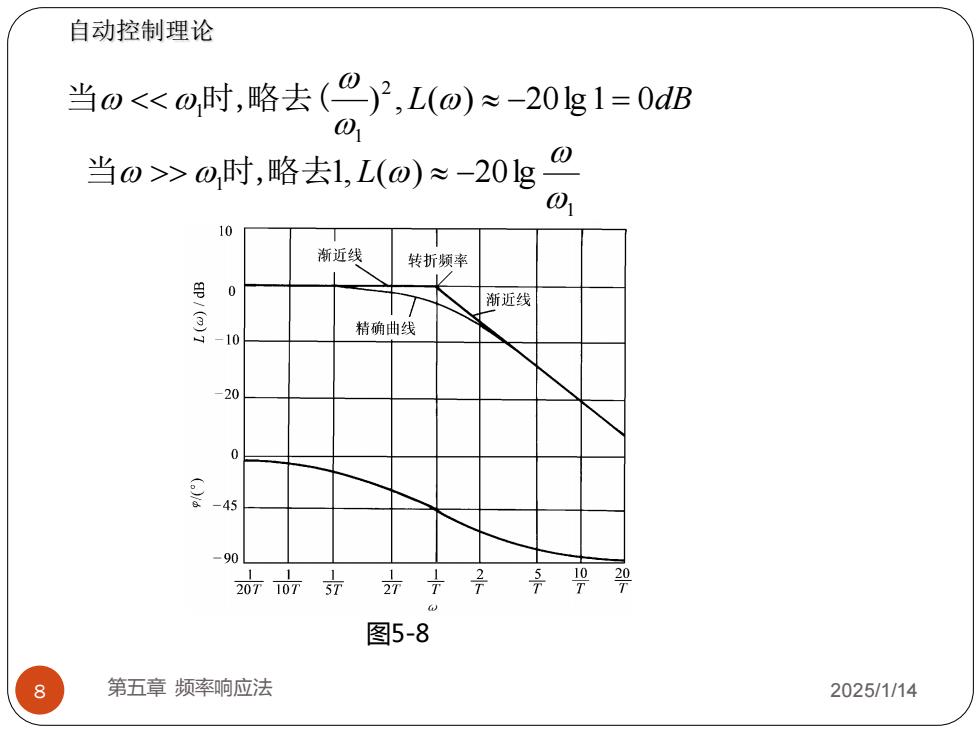
8 第五章 频率响应法 2025/1/14 ) , L( ) 20lg1 0dB 2 1  1   − =   当 时,略去( 1 1 1, ( ) 20lg   当 时,略去 L   − 图5-8 自动控制理论

自动控制理论 由于(1+joT)与(1+joT)互为倒数，则有 20g+jo-20j 1 40 精确曲线 20 渐近线 g1+0=-ag7+o 1 渐近线 3.积分、微分因子 (o)干1 9 1 () 1)积分因子 jo 90 45 L(o)=-20lg0 0.01 图5-10 9 第五章频率响应法 2025/1/14

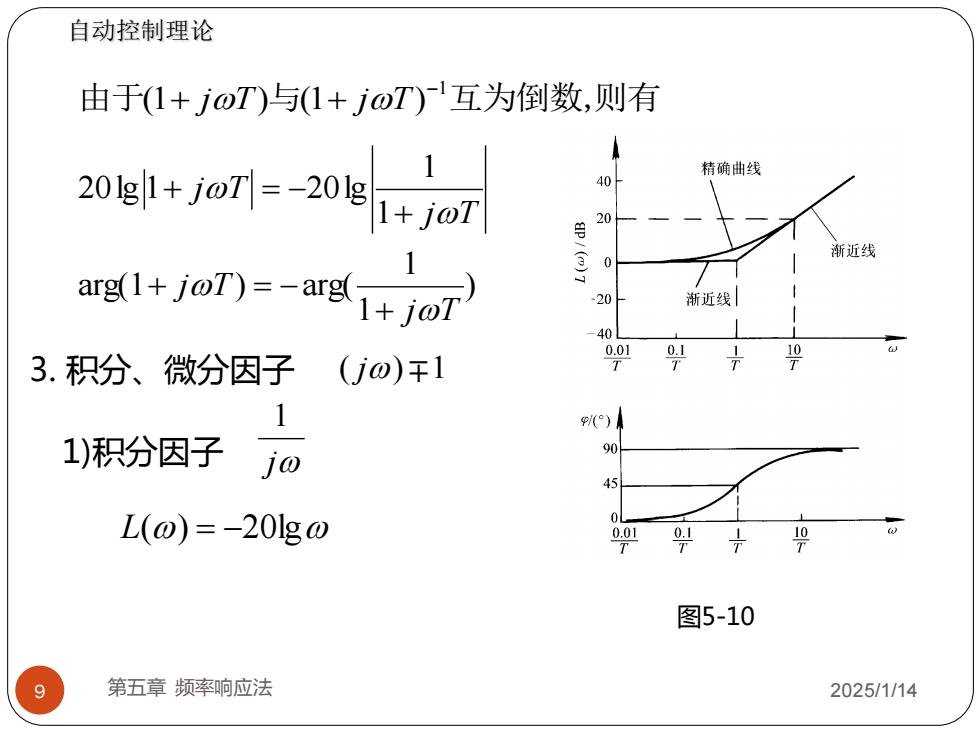
9 第五章 频率响应法 2025/1/14 L() = −20lg 由于(1+ jT)与(1+ jT) −1 互为倒数,则有 ) 1 1 arg(1 ) arg( 1 1 20lg 1 20lg j T j T j T j T     + + = − + + = − 图5-10 自动控制理论 3. 积分、微分因子 j 1 1)积分因子 ( j) 1

自动控制理论 p(0)=-90° 40 40 20 2)微分因子jo -20dB/dee 20 20dB/dec ∠(o)=20lg0 -20 20 -40 40 10 0.1 10 100 p(2)=+90° is-l 0 180 3) (joy -0 90 18 0.1 10 100 10 10 L(@)=-20ylg @+201g K wls-I a) 图5-11 b) p(0)=-y90° w/s-1 0.10.20.40.8124 102040100200400 90 103 V=2、 70 V=l =0 50 30 03-0E 20dB/dec 10 60dB 0 10 图5-12 10 第五章频率响应法 2025/1/14

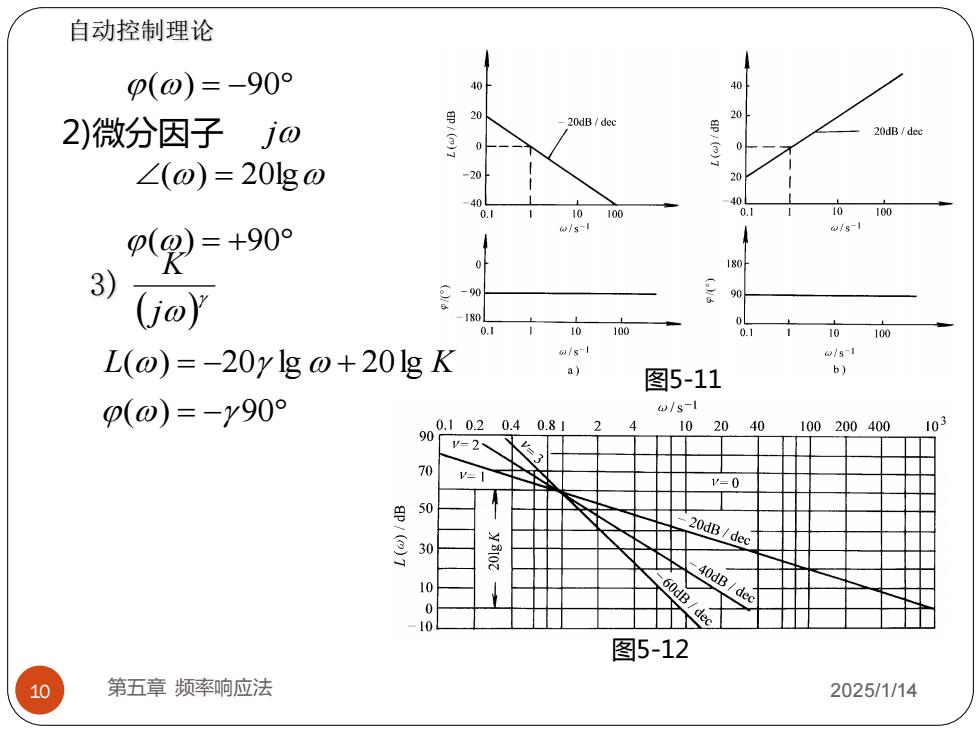
10 第五章 频率响应法 2025/1/14 () = −90 2)微分因子 j () = 20lg () = +90 图5-11 自动控制理论 3) ( )  j K = −  = − + ( ) 90 ( ) 20 lg 20lg    L    K 图5-12