
概率伦与款程统外 (2)利用公式计算 D(X)=EX-E(X) D(X)=E(X2)-E(X)2
( ) ( ) [ ( )] . 2 2 D X = E X − E X (2) 利用公式计算 ( ) {[ ( )] } 2 D X = E X − E X
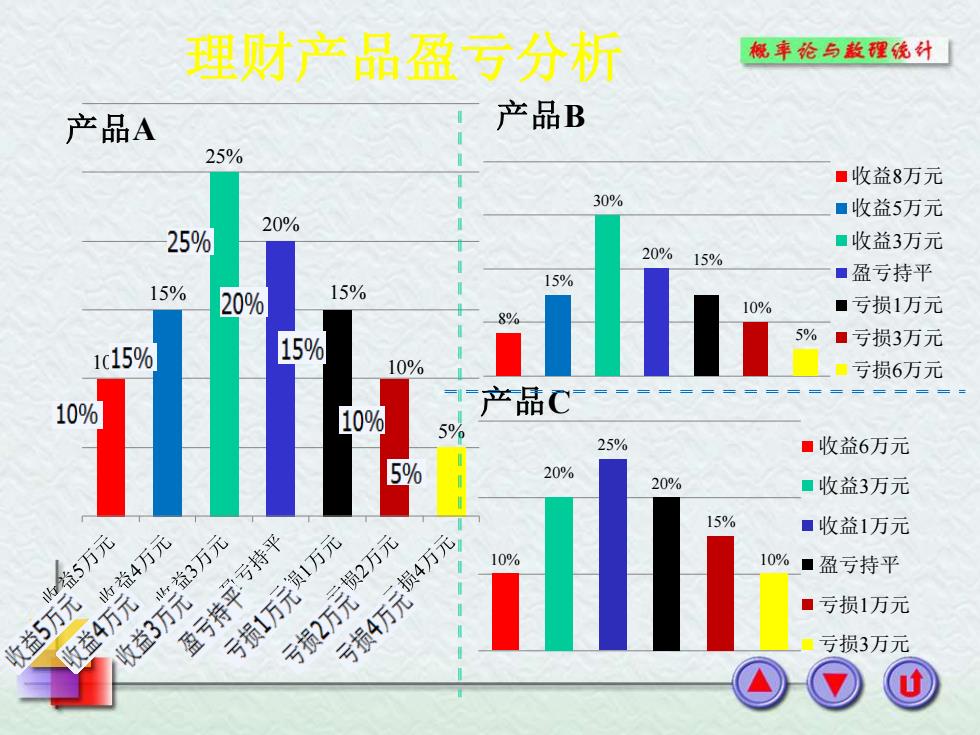
理财产品盈亏分析 概车纶与款理统外 产品A 产品B 25% ■收益8万元 30% ■收益5万元 20% 25% 20%15% ■收益3万元 15% ■盈亏持平 15% 20% 15% 10% ■亏损1万元 8% 5% ■亏损3万元 1c15% 15% 10% 亏损6万元 10% 产品C 10% 5% 25% ■收益6万元 5% 20% 20% ■收益3万元 15% ■收益1万元 收益4万元地益3万元 5万元 10% 10%■盈亏持平 收益5万元 的益4万元 盈亏持平亏持平 收益3万元 亏损2万元损2万元 亏损1万元员1万元 亏损4万元损4万元 ■亏损1万元 。亏损3万元
理财产品盈亏分析 10% 15% 25% 20% 15% 10% 5% 产品A 8% 15% 30% 20% 15% 10% 5% 产品B 收益8万元 收益5万元 收益3万元 盈亏持平 亏损1万元 亏损3万元 亏损6万元 10% 20% 25% 20% 15% 10% 产品C 收益6万元 收益3万元 收益1万元 盈亏持平 亏损1万元 亏损3万元

引入随机变量 概率伦与数醒统外 品B 产品A 收益:Y 收益:X ·收益8万元 30% ■收益5万元 25% 20%15% ■收益3万元 0.25 15% ■盈亏持平 0.20 10% ·亏损1万元 8% 5% ·亏损3万元 0.15 0.15。 ■亏损6万元 0.10 0.15 产品C 收益:Z 1u/0 ■收益6万元 0.05 25% 5% 20% ■收益3万元 20% ■收益1万元 15% ■盈亏持平 10% 10% 万元 2万元 ■亏损1万元 ■亏损3万元
10% 15% 25% 20% 15% 10% 5% 产品A 8% 15% 30% 20% 15% 10% 5% 产品B 收益8万元 收益5万元 收益3万元 盈亏持平 亏损1万元 亏损3万元 亏损6万元 10% 20% 25% 20% 15% 10% 产品C 收益6万元 收益3万元 收益1万元 盈亏持平 亏损1万元 亏损3万元 收益:𝑿 收益:Y 收益:Z 引入随机变量 0.10 0.15 0.25 0.20 0.15 0.15 0.05
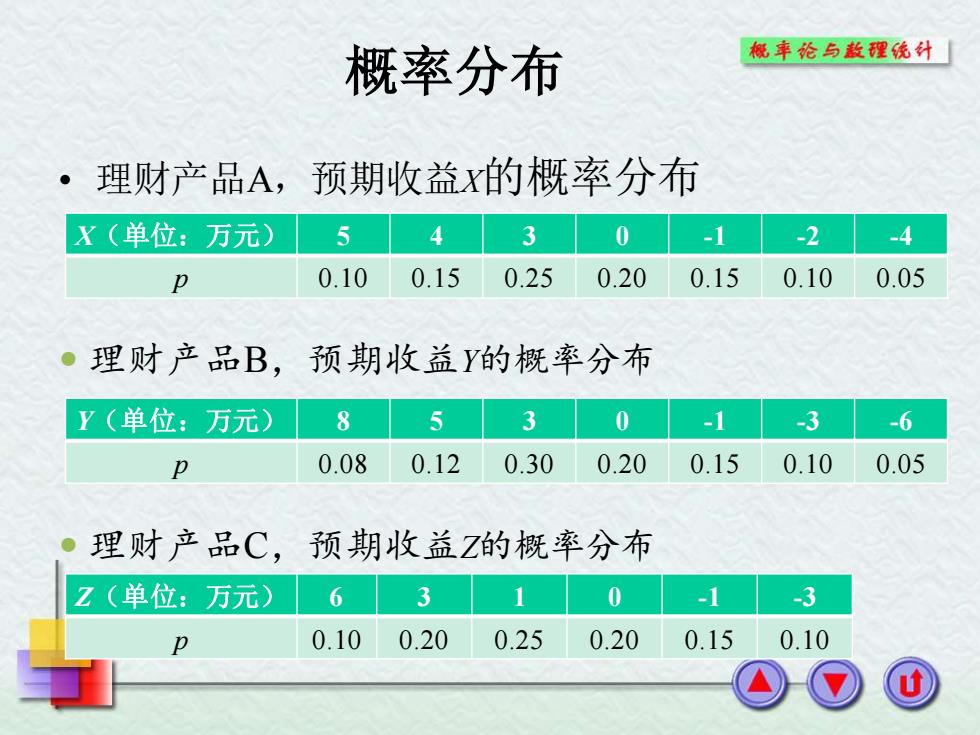
概率分布 概车纶与款理统外 。理财产品A, 预期收益x的概率分布 X(单位:万元) 5 4 3 0 1 -2 4 p 0.10 0.15 0.25 0.20 0.15 0.10 0.05 。理财产品B,预期收益Y的概率分布 Y(单位:万元) 8 5 3 0 -1 -3 -6 p 0.08 0.12 0.30 0.20 0.15 0.10 0.05 理财产品C,预期收益Z的概率分布 Z(单位:万元) 6 3 1 0 -1 -3 0.10 0.20 0.25 0.20 0.15 0.10
概率分布 • 理财产品A,预期收益X的概率分布 X(单位:万元) 5 4 3 0 -1 -2 -4 p 0.10 0.15 0.25 0.20 0.15 0.10 0.05 理财产品B,预期收益Y的概率分布 Y(单位:万元) 8 5 3 0 -1 -3 -6 p 0.08 0.12 0.30 0.20 0.15 0.10 0.05 理财产品C,预期收益Z的概率分布 Z(单位:万元) 6 3 1 0 -1 -3 p 0.10 0.20 0.25 0.20 0.15 0.10

概華论与款程统外 数学期望(均值)是什么? ·数学意义:数学期望由随机变量的取值与 其对应的概率加权平均得到,因此称之为 均值,它反映的是随机变量取值的平均水 平。 ·经济意义:数学期望是投资者所“期望” 获得的预期收益,因此称之为数学期望 它代表了“风险投资”中投资者预期的平 均收益
数学期望(均值)是什么? • 数学意义:数学期望由随机变量的取值与 其对应的概率加权平均得到,因此称之为 均值,它反映的是随机变量取值的平均水 平。 • 经济意义:数学期望是投资者所“期望” 获得的预期收益,因此称之为数学期望, 它代表了“风险投资”中投资者预期的平 均收益